人教版六年级下册数学第6单元:数学思考教学课件(34张)
文档属性
| 名称 | 人教版六年级下册数学第6单元:数学思考教学课件(34张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-25 19:59:43 | ||
图片预览









文档简介
(共34张PPT)
专题四 数学思考
RJ 六年级下册
解决逻辑推理题问题常用什么方法?
用等量代换的方法可以解决什么问题?
(1)运用数形结合的思想找规律
(2)列表法解决逻辑推理问题
(3)用“等量代换”法解决问题
(4)用几何知识进行简单的说理
课后作业
知识梳理
深化知识
拓展延伸
6个点可以连多少条线段?8个点呢?根据规律,你知道12个点、20个点能连多少条线段吗?请写出算式。想一想,n个点能连多少条线段?
两个点能连1条线段,也就是说每两个点之间都能连1条线段。可以从2个点开始,逐渐增加点数,找出能连成线段条数的规律。
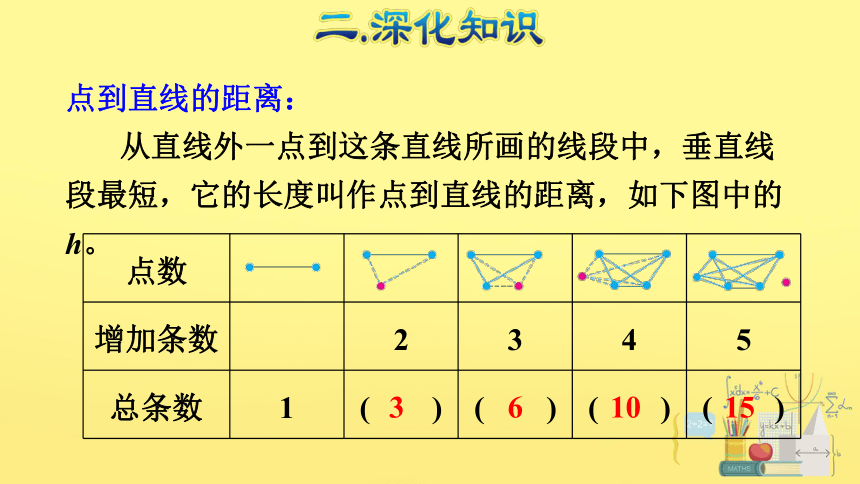
点到直线的距离:
从直线外一点到这条直线所画的线段中,垂直线段最短,它的长度叫作点到直线的距离,如下图中的h。
3
6
10
15
点数
增加条数 2 3 4 5
总条数 1 ( ) ( ) ( ) ( )
观察表格发现:从2个点开始,以后每增加1个点,这个点和原来的每个点连成1条线段,所以原来有几个点,就会相应增加几条线段。即:
1个点连成线段的条数:0条
2个点连成线段的条数:1条
3个点连成线段的条数:1+2=3(条)
4个点连成线段的条数:1+2+3=6(条)
5个点连成线段的条数:1+2+3+4=10(条)
从而找出规律:有几个点,连成线段的条数就是几之前的所有( )之和。
自然数
规范解答:
6个点连成线段的条数:
1+2+3+4+5=(1+5)×5÷2=15(条)
8个点连成线段的条数:
1+2+3+4+5+6+7=(1+7)×7÷2=28(条)
12个点连成线段的条数:
1+2+3+4+5+6+7+8+9+10+11
=(1+11)×11÷2=66(条)
规范解答:
20个点连成线段的条数:
1+2+3+4+5+6+……+18+19
=(1+19)×19÷2=190(条)
1.现有黑色三角形“▲”和白色三角形“△”共200个,按照一定规律排列如下。
▲▲△△▲△▲▲△△▲△▲▲……
则黑色三角形有( )个,白色三角形有( )个。
101
99
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
这是一道逻辑推理题,解决这种问题常用的方法是
( )法和( )法,有时利用( )、( )等方法,可使推理简便。
排除
假设
画图
列表
方法一:列表法。用数字“1”表示到会,用数字“0”表示没到会。
A B C D E F
第1次 1 1 1 0 0 0
第2次 0 1 0 1 1 0
第3次 1 0 0 0 1 1
从第一次到会的情况可以看出,A只可能和D、E、F同班;从第二次到会的情况可以判断,A只可能和D、E同班;从第三次到会的情况可以确定,A只可能和D同班。
从第一次到会情况可看出B可能和E、F同班,从第二次到会的情况可以看出B和F同班,从而可知C和E同班。
方法二:排除法。
从A考虑,由第一次和第三次到会情况,可知A不和B、C、E、F同班,所以A和D同班;
从B考虑,由第一次和第二次到会情况,可知B不和A、C、D、E同班,所以B和F同班;从而可知C和E同班。
甲、乙、丙、丁四人同时参加一次数学竞赛,赛后,他们四人预测名次的谈话如下:甲:“丙第一名,我第三名。”乙:“我第一名,丁第四名。”丙:“丁第二名,我第三名。”丁没有说话,最后公布结果时,发现他们的预测都只对了一半,请你说出这次比赛中甲、乙、丙、丁四人的名次。
甲第三,乙第一,丙第四,丁第二。
( )是指把一个量用与它相等的量去代替。它是数学中一种基本的思想方法。
等量代换
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
一个△等于3个□的和,把△+□=24中的△换成□+□+□,得到□+□+□+□=24,即4×□=24,所以□=6。把□=6代入△=□+□+□中,可算出△=6×3=18。
含有等号的式子叫做( )。等式的两边同时加或减去同一个数(或式子),等式两边仍然相等,这就是( )的性质1。等式两边同时乘同一个数(或式子),或除以同一个不为0的数(或式子),等式两边仍然相等;这就是( )的性质2。等式具有( )性,这是等式的性质3。如:a=b、b=c,那么a=b=c。
等式
等式
等式
传递
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
已知○+☆=160,◎+☆=160,根据等式的性质1,两个等式的两边都减去☆;得到○=160-☆,◎=160-☆,因为☆代表同一个数,所以○=◎。也可以这样想:由○+☆=160,◎+☆=160,根据等式的性质3,可知:○+☆=◎+☆,根据等式的性质1,等式两边同时减去☆,得到○=◎。
1. a、b、c各代表一个数,根据已知条件求a、b、c的值。
(1)a+b=54 a+c=27 b+c=30
a=( ) b=( ) c=( )
(2)a+b=18 a-b=10 c=a+a-b
a=( ) b=( ) c=( )
25.5
28.5
1.5
14
4
24
2. 什么是平角?平角与直线有什么区别?如右图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平角,
一共能组成几个平角?
(2)你能推出∠1=∠3吗?
平角与直线的区别:
端点
始
终
相反
度量
直线
射线
平角
平角 直线
区别 由一条射线绕它的( )旋转,当
( )边和( )边在同一条直线上,方向( )时,构成的角叫做平角。平角是一个角,可以( ),平角有一个顶点和两条边 把线段的两端无限延伸,就得到一条
( )。直线是一种线,直线不可度量,直线没有端点
联系 在直线上取一点,把直线分成了具有一个公共端点的两条( ),这时可把直线看成一个( )
(1)平角的两边在一条直线上,所以一共能组成4个平角。分别是:∠1和∠2组成的角,∠2和∠3组成的角,∠3和∠4组成的角,∠4和∠1组成的角。
(2)由∠1和∠2,∠2和∠3都能组成平角,可得到:∠1+∠2=180°,∠2+∠3=180°;根据等式的性质1,这两个等式的两边都减去∠2,得到∠1=180°-∠2,∠3=180°-∠2;因为180°-∠2=180°-∠2,所以∠1=∠3。也可以这样想:由∠1+∠2=180°,∠2+∠3=180°,根据等式的性质3,可知:∠1+∠2=∠2+∠3,根据等式的性质1,等式两边同时减去∠2,得到∠1=∠3。
1.学校阅览室有能坐4人的方桌,如果多于4人就把方桌拼成一行,2张方桌拼成一行最多能坐6人,如下图。
(1)将下表填写完整。
8
10
12
14
拼成一行的方桌数 1 2 3 4 5 6 …
最多能坐的人数 4 6 …
(2)10张方桌拼成一行最多能坐多少人?
(3)n(n≥1,且n为整数)张方桌拼成一行最多能坐多少人?(用含有n的式子表示)
10×2+2=22(人)
答:10张方桌拼成一行最多能坐22人。
2n+2
2.如下图,四边形ABCD是直角梯形,将BC边延长到点E。
(1)∠2和∠3拼成的是什么角?
(2)你能说明∠1=∠3吗?
∠2和∠3拼成的是平角。
因为四边形的内角和为360°,∠A和∠B都是直角,
所以∠1=360°-90°×2-∠2=180°-∠2。
因为∠2+∠3=180°,所以∠3=180°-∠2,
所以∠1=∠3。
3.钟楼的大钟5时整敲5下,用了28秒,那10时整,敲10下要多少秒?
28÷(5-1)×(10-1)=63(秒)
答:敲10下要63秒。
辨析:没有正确理解间隔问题的特征而引起解题错误。
4.鸡兔同笼,共有头53个,鸡的脚比兔的脚少98只。鸡、兔各有多少只?
假设全部是兔。
鸡:(53×4-98)÷(4+2)=19(只)
兔:53-19=34(只)
答:鸡有19只,兔有34只。
5.14个形状、大小一样的红球,其中一个重量较轻是不合格产品,至少用天平称几次能保证找出不合格产品?(请简要写出称的过程)
3次
作 业 从课后习题中选取。
专题四 数学思考
RJ 六年级下册
解决逻辑推理题问题常用什么方法?
用等量代换的方法可以解决什么问题?
(1)运用数形结合的思想找规律
(2)列表法解决逻辑推理问题
(3)用“等量代换”法解决问题
(4)用几何知识进行简单的说理
课后作业
知识梳理
深化知识
拓展延伸
6个点可以连多少条线段?8个点呢?根据规律,你知道12个点、20个点能连多少条线段吗?请写出算式。想一想,n个点能连多少条线段?
两个点能连1条线段,也就是说每两个点之间都能连1条线段。可以从2个点开始,逐渐增加点数,找出能连成线段条数的规律。
点到直线的距离:
从直线外一点到这条直线所画的线段中,垂直线段最短,它的长度叫作点到直线的距离,如下图中的h。
3
6
10
15
点数
增加条数 2 3 4 5
总条数 1 ( ) ( ) ( ) ( )
观察表格发现:从2个点开始,以后每增加1个点,这个点和原来的每个点连成1条线段,所以原来有几个点,就会相应增加几条线段。即:
1个点连成线段的条数:0条
2个点连成线段的条数:1条
3个点连成线段的条数:1+2=3(条)
4个点连成线段的条数:1+2+3=6(条)
5个点连成线段的条数:1+2+3+4=10(条)
从而找出规律:有几个点,连成线段的条数就是几之前的所有( )之和。
自然数
规范解答:
6个点连成线段的条数:
1+2+3+4+5=(1+5)×5÷2=15(条)
8个点连成线段的条数:
1+2+3+4+5+6+7=(1+7)×7÷2=28(条)
12个点连成线段的条数:
1+2+3+4+5+6+7+8+9+10+11
=(1+11)×11÷2=66(条)
规范解答:
20个点连成线段的条数:
1+2+3+4+5+6+……+18+19
=(1+19)×19÷2=190(条)
1.现有黑色三角形“▲”和白色三角形“△”共200个,按照一定规律排列如下。
▲▲△△▲△▲▲△△▲△▲▲……
则黑色三角形有( )个,白色三角形有( )个。
101
99
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
这是一道逻辑推理题,解决这种问题常用的方法是
( )法和( )法,有时利用( )、( )等方法,可使推理简便。
排除
假设
画图
列表
方法一:列表法。用数字“1”表示到会,用数字“0”表示没到会。
A B C D E F
第1次 1 1 1 0 0 0
第2次 0 1 0 1 1 0
第3次 1 0 0 0 1 1
从第一次到会的情况可以看出,A只可能和D、E、F同班;从第二次到会的情况可以判断,A只可能和D、E同班;从第三次到会的情况可以确定,A只可能和D同班。
从第一次到会情况可看出B可能和E、F同班,从第二次到会的情况可以看出B和F同班,从而可知C和E同班。
方法二:排除法。
从A考虑,由第一次和第三次到会情况,可知A不和B、C、E、F同班,所以A和D同班;
从B考虑,由第一次和第二次到会情况,可知B不和A、C、D、E同班,所以B和F同班;从而可知C和E同班。
甲、乙、丙、丁四人同时参加一次数学竞赛,赛后,他们四人预测名次的谈话如下:甲:“丙第一名,我第三名。”乙:“我第一名,丁第四名。”丙:“丁第二名,我第三名。”丁没有说话,最后公布结果时,发现他们的预测都只对了一半,请你说出这次比赛中甲、乙、丙、丁四人的名次。
甲第三,乙第一,丙第四,丁第二。
( )是指把一个量用与它相等的量去代替。它是数学中一种基本的思想方法。
等量代换
△、□、○、☆、◎各代表一个数。
(1)已知△+□=24,△=□+□+□。求△和□的值。
一个△等于3个□的和,把△+□=24中的△换成□+□+□,得到□+□+□+□=24,即4×□=24,所以□=6。把□=6代入△=□+□+□中,可算出△=6×3=18。
含有等号的式子叫做( )。等式的两边同时加或减去同一个数(或式子),等式两边仍然相等,这就是( )的性质1。等式两边同时乘同一个数(或式子),或除以同一个不为0的数(或式子),等式两边仍然相等;这就是( )的性质2。等式具有( )性,这是等式的性质3。如:a=b、b=c,那么a=b=c。
等式
等式
等式
传递
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
已知○+☆=160,◎+☆=160,根据等式的性质1,两个等式的两边都减去☆;得到○=160-☆,◎=160-☆,因为☆代表同一个数,所以○=◎。也可以这样想:由○+☆=160,◎+☆=160,根据等式的性质3,可知:○+☆=◎+☆,根据等式的性质1,等式两边同时减去☆,得到○=◎。
1. a、b、c各代表一个数,根据已知条件求a、b、c的值。
(1)a+b=54 a+c=27 b+c=30
a=( ) b=( ) c=( )
(2)a+b=18 a-b=10 c=a+a-b
a=( ) b=( ) c=( )
25.5
28.5
1.5
14
4
24
2. 什么是平角?平角与直线有什么区别?如右图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平角,
一共能组成几个平角?
(2)你能推出∠1=∠3吗?
平角与直线的区别:
端点
始
终
相反
度量
直线
射线
平角
平角 直线
区别 由一条射线绕它的( )旋转,当
( )边和( )边在同一条直线上,方向( )时,构成的角叫做平角。平角是一个角,可以( ),平角有一个顶点和两条边 把线段的两端无限延伸,就得到一条
( )。直线是一种线,直线不可度量,直线没有端点
联系 在直线上取一点,把直线分成了具有一个公共端点的两条( ),这时可把直线看成一个( )
(1)平角的两边在一条直线上,所以一共能组成4个平角。分别是:∠1和∠2组成的角,∠2和∠3组成的角,∠3和∠4组成的角,∠4和∠1组成的角。
(2)由∠1和∠2,∠2和∠3都能组成平角,可得到:∠1+∠2=180°,∠2+∠3=180°;根据等式的性质1,这两个等式的两边都减去∠2,得到∠1=180°-∠2,∠3=180°-∠2;因为180°-∠2=180°-∠2,所以∠1=∠3。也可以这样想:由∠1+∠2=180°,∠2+∠3=180°,根据等式的性质3,可知:∠1+∠2=∠2+∠3,根据等式的性质1,等式两边同时减去∠2,得到∠1=∠3。
1.学校阅览室有能坐4人的方桌,如果多于4人就把方桌拼成一行,2张方桌拼成一行最多能坐6人,如下图。
(1)将下表填写完整。
8
10
12
14
拼成一行的方桌数 1 2 3 4 5 6 …
最多能坐的人数 4 6 …
(2)10张方桌拼成一行最多能坐多少人?
(3)n(n≥1,且n为整数)张方桌拼成一行最多能坐多少人?(用含有n的式子表示)
10×2+2=22(人)
答:10张方桌拼成一行最多能坐22人。
2n+2
2.如下图,四边形ABCD是直角梯形,将BC边延长到点E。
(1)∠2和∠3拼成的是什么角?
(2)你能说明∠1=∠3吗?
∠2和∠3拼成的是平角。
因为四边形的内角和为360°,∠A和∠B都是直角,
所以∠1=360°-90°×2-∠2=180°-∠2。
因为∠2+∠3=180°,所以∠3=180°-∠2,
所以∠1=∠3。
3.钟楼的大钟5时整敲5下,用了28秒,那10时整,敲10下要多少秒?
28÷(5-1)×(10-1)=63(秒)
答:敲10下要63秒。
辨析:没有正确理解间隔问题的特征而引起解题错误。
4.鸡兔同笼,共有头53个,鸡的脚比兔的脚少98只。鸡、兔各有多少只?
假设全部是兔。
鸡:(53×4-98)÷(4+2)=19(只)
兔:53-19=34(只)
答:鸡有19只,兔有34只。
5.14个形状、大小一样的红球,其中一个重量较轻是不合格产品,至少用天平称几次能保证找出不合格产品?(请简要写出称的过程)
3次
作 业 从课后习题中选取。
