人教版六年级下册数学图形的认识与测量(1)课件(39张) (共39张PPT)
文档属性
| 名称 | 人教版六年级下册数学图形的认识与测量(1)课件(39张) (共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-25 00:00:00 | ||
图片预览






文档简介
(共39张PPT)
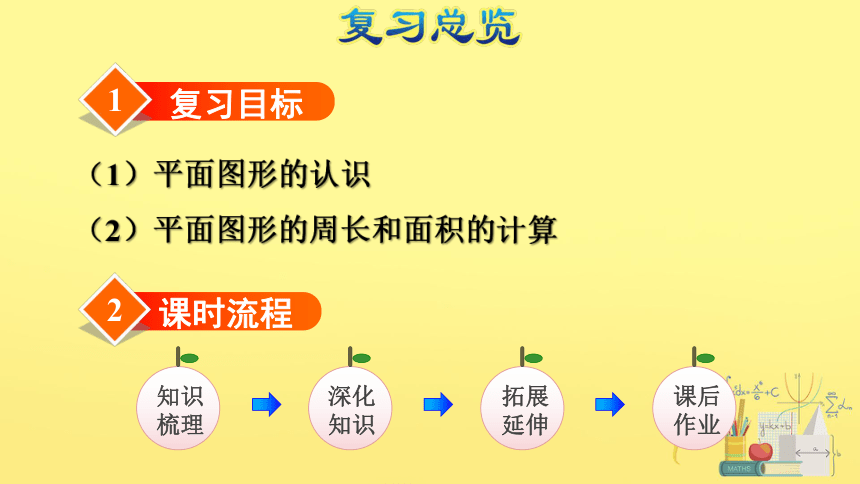
图形的认识与测量(1)
专题二 图形与几何
RJ 六年级下册
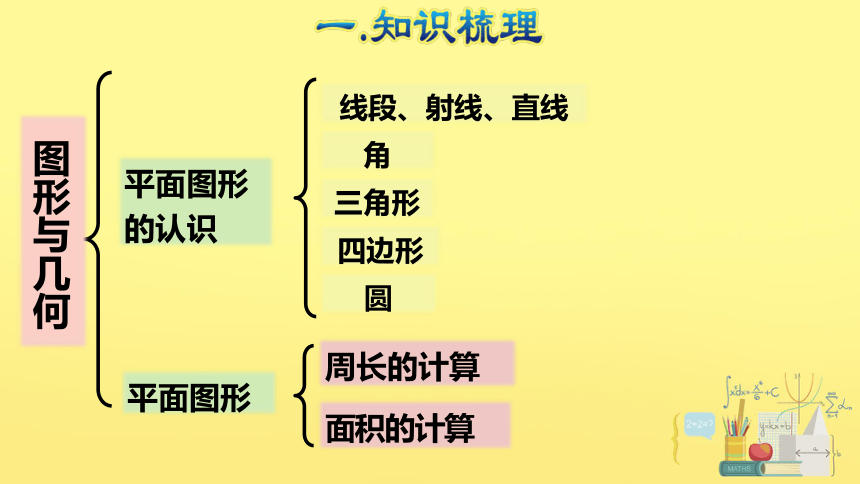
小学阶段我们学习了哪些平面图形?它们各自有什么特征?
(1)平面图形的认识
(2)平面图形的周长和面积的计算
知识梳理
深化知识
拓展延伸
课后作业
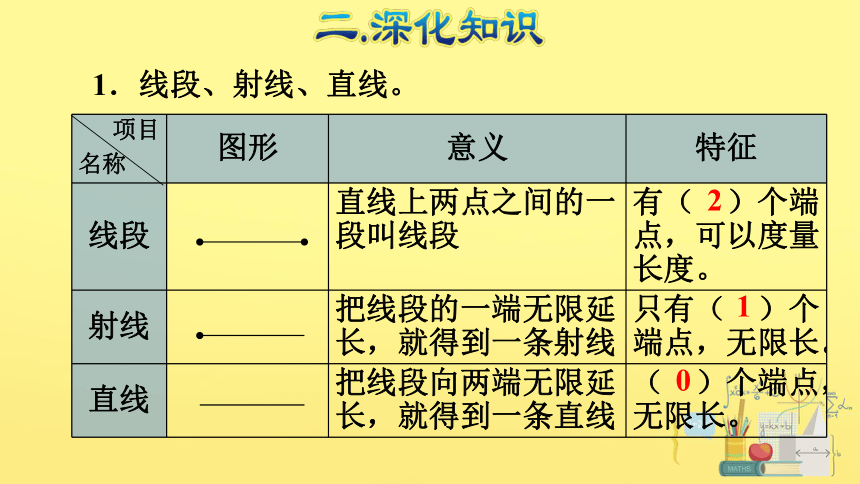
说一说,线段、射线、直线它们各自有什么特征?
1.线段、射线、直线。
2
1
0
项目
名称 图形 意义 特征
线段 直线上两点之间的一段叫线段 有( )个端点,可以度量长度。
射线 把线段的一端无限延长,就得到一条射线 只有( )个端点,无限长。
直线 把线段向两端无限延长,就得到一条直线 ( )个端点,无限长。
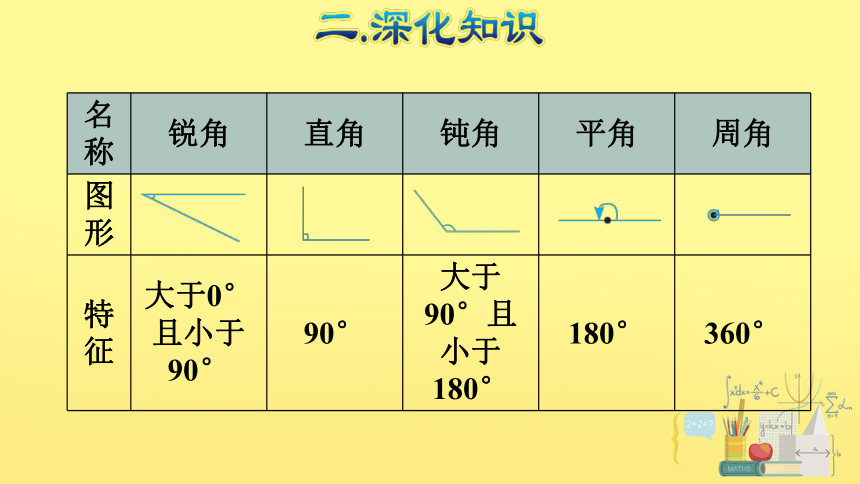
2.角:从一点引出两条( )所组成的图形叫作角。角通常用符号 “( )”来表示。
角的大小与两条边张开的大小有关。
射线
∠
名称 锐角 直角 钝角 平角 周角
图形
特征 大于0°且小于90° 90° 大于90°且小于180° 180° 360°
3.三角形:
由三条线段首尾顺次连接( )的图形叫作三角形。
从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫作三角形的高,这条对边叫作三角形的底。三角形有3 条高。
围成
任意三角形三边的关系:任意两边之和( )第三边,任意两边之差小于第三边。
三角形内角的关系:三角形内角和是( )°。
三角形的特性:具有( )性。
大于
180
稳定
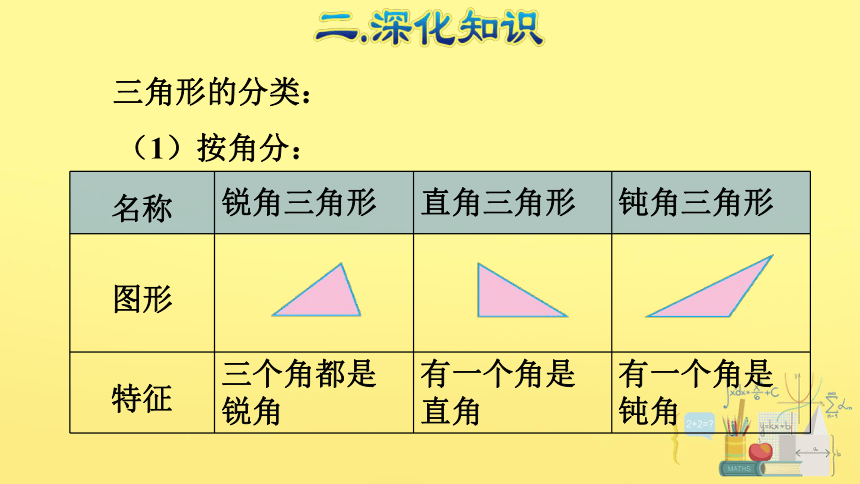
三角形的分类:
(1)按角分:
名称 锐角三角形 直角三角形 钝角三角形
图形
特征 三个角都是锐角 有一个角是直角 有一个角是钝角
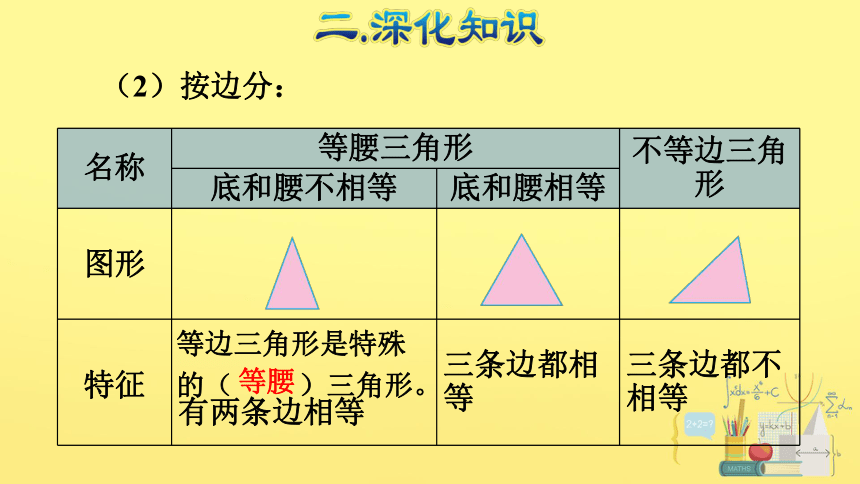
(2)按边分:
等边三角形是特殊的( )三角形。
等腰
名称 等腰三角形 不等边三角形
底和腰不相等 底和腰相等
图形
特征 有两条边相等 三条边都相等 三条边都不相等
4.四边形:
在同一平面内,由( )首尾顺次连接围成的封闭图形叫作四边形。
四条线段
(1)各种四边形的关系:
四边形
平行四边形
长方形
正方形
梯形
(2)已学过的四种特殊四边形的特征:
名称 长方形 正方形 平行四边形 梯形
图形
特征 对边平行且相等,四个角都是直角 对边平行,四条边都相等,四个角都是直角 对边平行
且相等 只有一组对边
平行
5.圆:圆是平面上封闭的曲线图形。
(1)圆的各部分名称:用圆规画圆时,针尖所在的点是( ),通常用字母O 表示;连接圆心和圆上任意一点的线段叫作( ),一般用字母r 表示;通过圆心并且两端都在圆上的线段叫作( ),一般用字母d 表示。
圆心
半径
直径
(2)圆心、半径与圆的关系:圆心决定圆的( ),半径决定圆的( )。
位置
大小
(3)圆的特征:
①在同一个圆中,可以画( )条半径、直径。
②在同一个圆中,直径的长度是半径的2 倍,可以表示为d=2r 或r= d。
③圆是轴对称图形,直径所在的直线是圆的对称轴, 圆有( )条对称轴。弧:下图中,
圆上A、B 两点之间的部分叫作弧,
读作“弧AB”。
无数
无数
扇形:一条弧和经过这条弧两端的两条半径所围成的图形,右图中涂色部分就是扇形。
圆心角:顶点在圆心的角,右图中的∠ AOB 就是一个圆心角。在同一个圆中,扇形的大小与这个扇形的圆心角的大小( )。
有关
(1)6 m28 dm2=( ) m2
0.05 km2=( ) hm2
(2)在边长为8 cm的正方形纸上剪一个最大的圆,该圆的半径是( )cm。
1.填空。
6.08
5
4
(3)钟面上3时整,时针和分针组成的角是( )。
(4)一个三角形的两条边的长分别是8 cm和12 cm,第三条边最长是( )cm,最短是( )cm。(边长为整厘米数)
(5)一个三角形的两个角分别是78°和27°,第三个角是( )°。
直角
19
5
75
2.判断。(对的画“√”,错的画“×”)
(1)直线都比射线长。 ( )
(2)大圆的圆周率比小圆的圆周率大。 ( )
(3)锐角三角形的两个锐角的和一定大于90°。 ( )
3.动手操作。
过D点画直线AB的平行线,画直线AC的垂线。
略
1.周长的意义:围成一个平面图形的一周的( )总和叫做这个图形的周长。周长一般用字母C表示,计量周长用长度单位。
长度
2.学过的平面图形的周长计算公式:
正方形的周长=( )×( ),用字母表示是:( )。
长方形的周长=( + )×2,用字母表示是:
( )。
圆的周长用字母表示是:( )或( )。
3 .面积的意义:围成平面图形的大小。
边长
4
C=4a
长 宽
C=2(a+b)
C=πd
C= 2πr
4 .学过的平面图形的面积计算公式(用字母表示):
正方形的面积:( )
长方形的面积:( )
平行四边形的面积:( )
三角形的面积:( )
梯形的面积:( )
圆的面积:( )
圆环的面积:( )
S=a2
S=ah
S=ah
S=ah÷2
S=(a+b)h÷2
S=πr2
S=π(R2-r2)
5. 面积计算公式的推导过程:
(1)平行四边形的面积计算公式推导过程:把平行四边形沿着一条( )剪开,再拼成一个( )形,拼成的长方形的长等于平行四边形的( ),宽等于平行四边形的( ),长方形的面积等于平行四边形的面积,因为长方形的面积=长×宽,所以平行四边形的面积=底×高。
高
长方
底
高
(2)三角形的面积计算公式推导过程:把两个( )的三角形拼成一个( )形,拼成的平行四边形的底等于三角形的( ),高等于三角形的( ),面积等于两个三角形的面积之和,因为平行四边形的面积=底×高,所以一个三角形的面积=底×高÷2。
完全一样
平行四边
底
高
(3)梯形的面积计算公式推导过程:把两个( )的梯形拼成一个( )形,拼成的平行的底等于梯形的( )的和,高等于梯形的( ),面积等于两个梯形的面积之和。因为平行四边形的面积=底×高,所以梯形的面积=(上底+下底)×高÷2。
完全一样
平行四边
上、下底
高
(4)圆的面积计算公式推导过程:把一个圆分成若干偶数等份,剪开后拼成一个近似的( )形,这个长方形的长相当于圆( ),宽相当于圆的( ),因为长方形的面积=长×宽,所以圆的面积=
( )×( ),即
S=πr2。
长方
周长的一半
半径
πr
r
6.
组合图形的面积:可以用( )求和的方法,也可用
( )求差的方法来计算
阴影部分的面积:可以直接利用图形的面积公式来求,也可以用整个图形的面积( )空白部分的面积来求,还可以利用求组合图形面积的方法计算
分割
添补
减去
6.
不规则图形的面积:可以把不规则的图形( )为学过的基本图形,然后根据面积公式来计算,也可以通过数方格的方法来估算
转化
1.填空。
(1)用一根铁丝围成一个长12 cm,宽6 cm的长方形。如果把它改围成一个正方形,围成的正方形的面积是( )cm2。
(2)一个三角形的面积是12.9 dm2,底长6 dm,高是( )dm。
81
4.3
(3)一个圆的直径是6 cm,这个圆的周长是( )cm,面积是( )cm2。
(4)用四根硬纸条订成一个长方形框架,将它拉成一个平行四边形后,周长( ),面积( )。
(5)一个直角梯形的上底长4 cm,下底和高都是10 cm,这个梯形的面积是( )cm2。
18.84
28.26
不变
变小
70
2.判断。(对的画“√”,错的画“×”)
(1)平行四边形的面积是三角形面积的2倍。 ( )
(2)两个面积相等的梯形一定能拼成一个平行四边形。 ( )
(3)半径为2 dm的圆,它的周长和面积相等。 ( )
(4)一个长方形的长和宽都增加4 cm,面积就增加16 cm2。 ( )
3.计算下面图形的周长或面积。
(1)计算下面图形的面积。
7×5=35(cm2)
①
7×10+5×4=90(cm2)
②
(2)计算下图中阴影部分的周长。
2×3.14=6.28(cm)
4.求下面半圆形的周长。(单位: cm)
3.14×12÷2+12=30.84(cm)
作 业 从课后习题中选取。
图形的认识与测量(1)
专题二 图形与几何
RJ 六年级下册
小学阶段我们学习了哪些平面图形?它们各自有什么特征?
(1)平面图形的认识
(2)平面图形的周长和面积的计算
知识梳理
深化知识
拓展延伸
课后作业
说一说,线段、射线、直线它们各自有什么特征?
1.线段、射线、直线。
2
1
0
项目
名称 图形 意义 特征
线段 直线上两点之间的一段叫线段 有( )个端点,可以度量长度。
射线 把线段的一端无限延长,就得到一条射线 只有( )个端点,无限长。
直线 把线段向两端无限延长,就得到一条直线 ( )个端点,无限长。
2.角:从一点引出两条( )所组成的图形叫作角。角通常用符号 “( )”来表示。
角的大小与两条边张开的大小有关。
射线
∠
名称 锐角 直角 钝角 平角 周角
图形
特征 大于0°且小于90° 90° 大于90°且小于180° 180° 360°
3.三角形:
由三条线段首尾顺次连接( )的图形叫作三角形。
从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫作三角形的高,这条对边叫作三角形的底。三角形有3 条高。
围成
任意三角形三边的关系:任意两边之和( )第三边,任意两边之差小于第三边。
三角形内角的关系:三角形内角和是( )°。
三角形的特性:具有( )性。
大于
180
稳定
三角形的分类:
(1)按角分:
名称 锐角三角形 直角三角形 钝角三角形
图形
特征 三个角都是锐角 有一个角是直角 有一个角是钝角
(2)按边分:
等边三角形是特殊的( )三角形。
等腰
名称 等腰三角形 不等边三角形
底和腰不相等 底和腰相等
图形
特征 有两条边相等 三条边都相等 三条边都不相等
4.四边形:
在同一平面内,由( )首尾顺次连接围成的封闭图形叫作四边形。
四条线段
(1)各种四边形的关系:
四边形
平行四边形
长方形
正方形
梯形
(2)已学过的四种特殊四边形的特征:
名称 长方形 正方形 平行四边形 梯形
图形
特征 对边平行且相等,四个角都是直角 对边平行,四条边都相等,四个角都是直角 对边平行
且相等 只有一组对边
平行
5.圆:圆是平面上封闭的曲线图形。
(1)圆的各部分名称:用圆规画圆时,针尖所在的点是( ),通常用字母O 表示;连接圆心和圆上任意一点的线段叫作( ),一般用字母r 表示;通过圆心并且两端都在圆上的线段叫作( ),一般用字母d 表示。
圆心
半径
直径
(2)圆心、半径与圆的关系:圆心决定圆的( ),半径决定圆的( )。
位置
大小
(3)圆的特征:
①在同一个圆中,可以画( )条半径、直径。
②在同一个圆中,直径的长度是半径的2 倍,可以表示为d=2r 或r= d。
③圆是轴对称图形,直径所在的直线是圆的对称轴, 圆有( )条对称轴。弧:下图中,
圆上A、B 两点之间的部分叫作弧,
读作“弧AB”。
无数
无数
扇形:一条弧和经过这条弧两端的两条半径所围成的图形,右图中涂色部分就是扇形。
圆心角:顶点在圆心的角,右图中的∠ AOB 就是一个圆心角。在同一个圆中,扇形的大小与这个扇形的圆心角的大小( )。
有关
(1)6 m28 dm2=( ) m2
0.05 km2=( ) hm2
(2)在边长为8 cm的正方形纸上剪一个最大的圆,该圆的半径是( )cm。
1.填空。
6.08
5
4
(3)钟面上3时整,时针和分针组成的角是( )。
(4)一个三角形的两条边的长分别是8 cm和12 cm,第三条边最长是( )cm,最短是( )cm。(边长为整厘米数)
(5)一个三角形的两个角分别是78°和27°,第三个角是( )°。
直角
19
5
75
2.判断。(对的画“√”,错的画“×”)
(1)直线都比射线长。 ( )
(2)大圆的圆周率比小圆的圆周率大。 ( )
(3)锐角三角形的两个锐角的和一定大于90°。 ( )
3.动手操作。
过D点画直线AB的平行线,画直线AC的垂线。
略
1.周长的意义:围成一个平面图形的一周的( )总和叫做这个图形的周长。周长一般用字母C表示,计量周长用长度单位。
长度
2.学过的平面图形的周长计算公式:
正方形的周长=( )×( ),用字母表示是:( )。
长方形的周长=( + )×2,用字母表示是:
( )。
圆的周长用字母表示是:( )或( )。
3 .面积的意义:围成平面图形的大小。
边长
4
C=4a
长 宽
C=2(a+b)
C=πd
C= 2πr
4 .学过的平面图形的面积计算公式(用字母表示):
正方形的面积:( )
长方形的面积:( )
平行四边形的面积:( )
三角形的面积:( )
梯形的面积:( )
圆的面积:( )
圆环的面积:( )
S=a2
S=ah
S=ah
S=ah÷2
S=(a+b)h÷2
S=πr2
S=π(R2-r2)
5. 面积计算公式的推导过程:
(1)平行四边形的面积计算公式推导过程:把平行四边形沿着一条( )剪开,再拼成一个( )形,拼成的长方形的长等于平行四边形的( ),宽等于平行四边形的( ),长方形的面积等于平行四边形的面积,因为长方形的面积=长×宽,所以平行四边形的面积=底×高。
高
长方
底
高
(2)三角形的面积计算公式推导过程:把两个( )的三角形拼成一个( )形,拼成的平行四边形的底等于三角形的( ),高等于三角形的( ),面积等于两个三角形的面积之和,因为平行四边形的面积=底×高,所以一个三角形的面积=底×高÷2。
完全一样
平行四边
底
高
(3)梯形的面积计算公式推导过程:把两个( )的梯形拼成一个( )形,拼成的平行的底等于梯形的( )的和,高等于梯形的( ),面积等于两个梯形的面积之和。因为平行四边形的面积=底×高,所以梯形的面积=(上底+下底)×高÷2。
完全一样
平行四边
上、下底
高
(4)圆的面积计算公式推导过程:把一个圆分成若干偶数等份,剪开后拼成一个近似的( )形,这个长方形的长相当于圆( ),宽相当于圆的( ),因为长方形的面积=长×宽,所以圆的面积=
( )×( ),即
S=πr2。
长方
周长的一半
半径
πr
r
6.
组合图形的面积:可以用( )求和的方法,也可用
( )求差的方法来计算
阴影部分的面积:可以直接利用图形的面积公式来求,也可以用整个图形的面积( )空白部分的面积来求,还可以利用求组合图形面积的方法计算
分割
添补
减去
6.
不规则图形的面积:可以把不规则的图形( )为学过的基本图形,然后根据面积公式来计算,也可以通过数方格的方法来估算
转化
1.填空。
(1)用一根铁丝围成一个长12 cm,宽6 cm的长方形。如果把它改围成一个正方形,围成的正方形的面积是( )cm2。
(2)一个三角形的面积是12.9 dm2,底长6 dm,高是( )dm。
81
4.3
(3)一个圆的直径是6 cm,这个圆的周长是( )cm,面积是( )cm2。
(4)用四根硬纸条订成一个长方形框架,将它拉成一个平行四边形后,周长( ),面积( )。
(5)一个直角梯形的上底长4 cm,下底和高都是10 cm,这个梯形的面积是( )cm2。
18.84
28.26
不变
变小
70
2.判断。(对的画“√”,错的画“×”)
(1)平行四边形的面积是三角形面积的2倍。 ( )
(2)两个面积相等的梯形一定能拼成一个平行四边形。 ( )
(3)半径为2 dm的圆,它的周长和面积相等。 ( )
(4)一个长方形的长和宽都增加4 cm,面积就增加16 cm2。 ( )
3.计算下面图形的周长或面积。
(1)计算下面图形的面积。
7×5=35(cm2)
①
7×10+5×4=90(cm2)
②
(2)计算下图中阴影部分的周长。
2×3.14=6.28(cm)
4.求下面半圆形的周长。(单位: cm)
3.14×12÷2+12=30.84(cm)
作 业 从课后习题中选取。
