2020春华师版九下数:几何的回顾几何问题的处理方法第2课时课件(38张PPT)
文档属性
| 名称 | 2020春华师版九下数:几何的回顾几何问题的处理方法第2课时课件(38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 775.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 18:28:26 | ||
图片预览










文档简介
课件38张PPT。第2课时1.平行四边形的性质.
(1)平行四边形两组对边分别_____且_____;
(2)平行四边形两组对角分别_____;
(3)平行四边形对角线互相_____.平行相等相等平分2.矩形、菱形和正方形的性质.
(1)矩形的性质
①矩形的四个角都是_____;
②矩形的对角线_______________.
(2)菱形的性质
①菱形的四条边都_____;
②菱形的对角线互相_____,并且每条对角线_____一组对角.
(3)正方形具有_____与_____的所有性质.直角相等且互相平分相等垂直平分矩形菱形3.等腰梯形的性质.
(1)等腰梯形_______上的两个内角相等;
(2)等腰梯形的_______相等.同一底对角线【预习思考】
1.平行四边形的定义和性质在几何证明中的作用是什么?
提示:平行四边形的定义和性质是今后证明线段相等、两角相
等、两直线平行或垂直的重要依据.2.研究平行四边形的规律方法:
提示:在研究平行四边形所具有的特性(即性质)及平行四边形
的识别(即判定)时,应用数形结合、转化等数学思想,将其转化
为三角形问题,借助三角形的相关知识使平行四边形的性质和判
定得以展现. 平行四边形判定与性质的应用
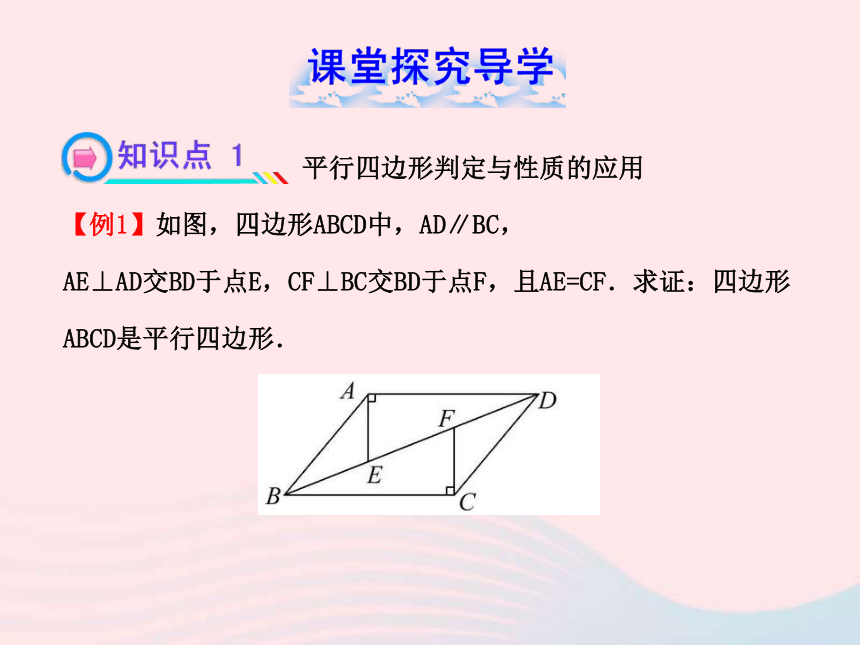
【例1】如图,四边形ABCD中,AD∥BC,
AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形
ABCD是平行四边形.【解题探究】(1)试证明△ADE≌△CBF.
证明:∵AD∥BC,
∴∠ADB= ∠CBD.
∵AE⊥AD,CF⊥BC,
∴ ∠EAD = ∠FCB =90°.
∵AE=CF,∴△ADE≌△CBF,(2)AD和BC相等吗?
答:AD=BC.
(3)∵AD____BC,∴四边形ABCD是平行四边形. 【规律总结】
平行四边形的五种判定方法
1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.一组对边平行且相等的四边形是平行四边形;
4.对角线互相平分的四边形是平行四边形;
5.两组对角分别相等的四边形是平行四边形.【跟踪训练】
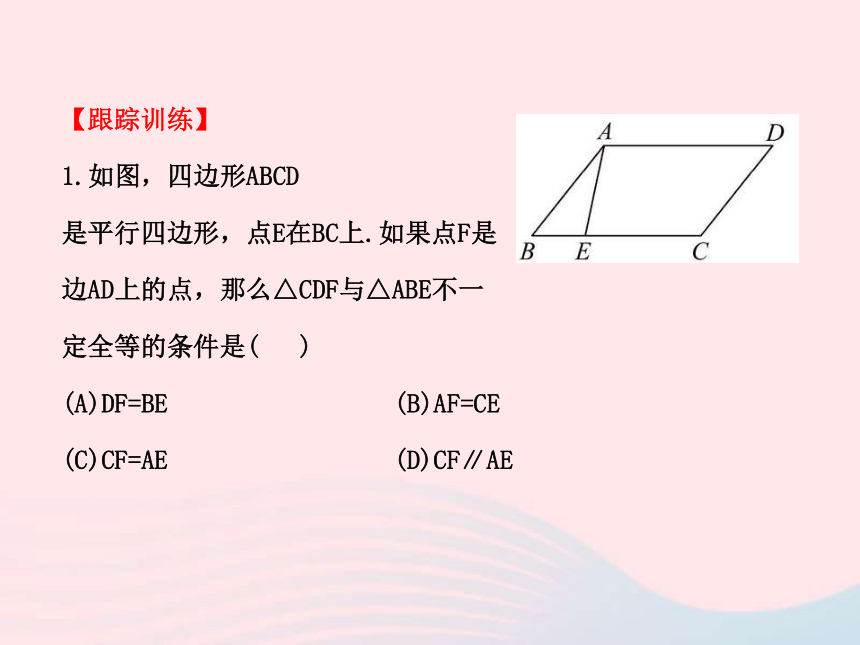
1.如图,四边形ABCD
是平行四边形,点E在BC上.如果点F是
边AD上的点,那么△CDF与△ABE不一
定全等的条件是( )
(A)DF=BE (B)AF=CE
(C)CF=AE (D)CF∥AE【解析】选C.结合平行四边形性质,如果DF=BE,则与∠D=∠B,
CD=AB,恰好满足(S.A.S.)全等条件,即△CDF≌△ABE;如果
AF=CE,因为AD=CB,所以DF=BE,结合选项A,能够判断△CDF≌
△ABE;如果CF=AE,判断两三角形全等条件不具备;如果CF∥AE,
则四边形AECF是平行四边形,则有AF=CE,结合选项B,能够判断
△CDF≌△ABE.2.如图,在□ABCD中,
∠A=70°,将□ABCD折叠,使点D,C分
别落在点F,E处(点F,E都在AB所在的
直线上),折痕为MN,则∠AMF等于( )
(A)70° (B)40°
(C)30° (D)20°
【解析】选B.由□ABCD折叠得∠DMN=∠NMF=∠A=70°,
∴∠AMF=180°-70°-70°=40°. 殊平行四边形的性质与判定
【例2】如图,
在△ABC中,点O是AC边上(端点除外)
的一个动点,过点O作直线MN∥BC.
设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连结AE,
AF.那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
易错提醒:不要忘记把OA=OC作为已知条件运用!【规范解答】当点O运动到AC的中点(或OA=OC)时,
四边形AECF是矩形.………………………………………2分
理由如下:
∵CE平分∠BCA,∴∠1=∠2.
........................3分
又∵MN∥BC,∴∠1= ∠3 .
∴ ∠3 =∠2,∴ EO =CO………………………………………5分同理,FO=CO …………………………………………………6分
∴EO=FO.又OA=OC,
∴四边形AECF是平行四形……………………………………7分
又∵∠1=∠2,∠4=∠5,
∴∠1+∠5=∠2+∠4 …………………………………………8分
又∵∠1+∠5+∠2+∠4=180,
∴∠2+∠4=90°………………………………………………9分
∴四边形AECF是矩形…………………………………………10分【规律总结】
判定正方形常出现的三种错误
1.四条边相等就直接判定为正方形;
2.四个角为直角就判定为正方形;
3.对角线相等且垂直就判定为正方形.【跟踪训练】
3.已知菱形ABCD中,对角线AC与BD相交于点
O,∠BAD=120°,AC=4,则该菱形的面积是( )
(A) (B)16 (C) (D)8
【解析】选C. 因为∠BAD=120°,所以∠ABC=60°,所以菱形被
分成两个等边三角形,因为AC=4,故 所以BD=
面积4.点P是正方形ABCD
边AB上一点(不与A,B重合),连结PD并
将线段PD绕点P顺时针旋转90°,得线
段PE,连结BE,则∠CBE等于( )
(A)75° (B)60°
(C)45° (D)30°【解析】选C.延长AB,过E作AB的延长
线的垂线交于点F,由线段PD绕点P顺时
针旋转90°得线段PE,可知DP= EP ,
∠DPE=90°,所以∠EPF+∠DPA=
90°,而∠ADP+∠DPA=90°,所以∠EPF= ∠ADP.
又因为∠DAP=∠PFE=90°,所以△ADP≌△FPE,所以AP=FE,
AD=FP=AB,所以BF+PB=AP+PB,所以BF=AP,所以FE=BF,
所以∠EBF=∠BEF=45°,
所以∠CBE=90°-45°=45°. 等腰梯形的性质与判定
【例3】(6分)如图在等腰梯形ABCD中,AD∥BC,∠C=60°,AD=10,AB=18,求BC的长.【规范解答】
如图,过D点作DE∥AB交BC于E.
………………………………2分
∵AD∥BC,∴BE=AD=10,
DE=AB=DC=18,…………………………………………………4分
∵∠B=∠C=60°,∴EC=DC=DE=18,
∴BC=BE+EC=10+18=28.………………………………………6分【一题多解】方法一:如图,分别过A,D两点作AE⊥BC,DF⊥BC,垂足分别为E和F,
∵AD∥BC,AB=CD,
∴∠B=∠C=60°,EF=AD=10,∠BAE=∠CDF=30°,
∴Rt△ABE≌Rt△DCF,
∴BE=CF= AB=9,
∴BC=BE+EF+FC=9+10+9=28.方法二:如图,分别延长BA,CD交于点E.
∵AD∥BC,AB=CD,
∴∠B=∠C=60°,∠EAD=∠EDA,
∴△EBC与△EAD均为等边三角形,
∴BC=BE=AB+AE=AB+AD=18+10=28.方法三:如图,过点C作CE∥BA交AD的延长线于点E.
∵AD∥BC,∴四边形ABCE是平行四边形,
∠BCD=∠CDE=60°,又∠B=∠E=60°,
∴AB=EC=DC=18,
∴△DEC是等边三角形,∴DE=AB=18,
∴BC=AD+DE=10+18=28.【规律总结】
梯形常作辅助线“五种方法”
1.“平移腰”:把梯形分成一个平行四边形和一个三角形;
2.“作高”:使两腰在两个直角三角形中;
3.“平移对角线”:使两条对角线在同一个三角形中;
4.“延腰”:构造具有公共角的两个等腰三角形;
5.“等积变形”:连结梯形上底一端点和另一腰中点,并延长与下
底延长线交于一点,构成三角形.【跟踪训练】
5.如图,在梯形ABCD中,AB∥DC,AD=DC=CB,若
∠ABD=25°,则∠BAD的大小是( )
(A)40° (B)45°
(C)50° (D)60°
【解析】选C.由CB=DC,AB∥DC可得∠CBD=∠CDB=∠ABD=25°,得
到∠CBA=50°,由等腰梯形可得∠BAD=∠CBA=50°.6.如图,在平面直角
坐标系中,等腰梯形ABCD的下底在x轴
上,且B点坐标为(4,0),D点坐标为
(0,3),则AC长为( )
(A)4 (B)5 (C)6 (D)不能确定【解析】选B.如图,连结BD,
由题意得,OB=4,OD=3, 故可得BD=5.
又四边形ABCD是等腰梯形,
∴AC=BD=5.7.如图,等腰梯形ABCD
中,AD∥BC,点E是AD延长线上的一点,
且CE=CD,求证:∠B=∠E.
【证明】∵四边形ABCD为等腰梯形,AD∥BC,
∴∠B=∠BCD,∠BCD=∠CDE,∴∠B=∠CDE.
又∵CD=CE,∴∠CDE=∠E,∴∠B=∠E.1.如图,矩形ABCD的对角线AC,BD相
交于点O,CE∥BD,DE∥AC,若AC=4,
则四边形CODE的周长是( )
(A)4 (B)6 (C)8 (D)10
【解析】选C.∵CE∥BD,DE∥AC,∴四边形CODE为平行四边形.
又∵四边形ABCD为矩形,∴OD=OC=2,∴四边形CODE为菱形,其周
长为2×4=8.2.如图,菱形ABCD的周长是16,∠A=60°,则对
角线BD的长度为( )
(A)2 (B)
(C)4 (D)
【解析】选C.∵菱形ABCD的周长是16, ∴AB=BC=CD=DA=4,
∵∠A=60°,∴BD=AB=DA=4.3.如图,等腰梯形ABCD中,
AD∥BC,AB=AD=2,∠B=60°,则BC的长为_____.
【解析】作AE⊥BC,DF⊥BC,则EF=AD=2,
又∠B=60°,所以∠BAE=30°,
故BE= AB=1.同理,FC=1.
所以BC=BE+EF+FC=1+2+1=4.
答案:44.矩形ABCD的对角
线相交于点O,AB=4 cm,∠AOB=60°,
则矩形的面积为_____cm2.
【解析】根据矩形的性质得出AC=BD,OA= AC, OB= BD推出
OA=OB,得到等边三角形ABO,求出AC,由∠ABC=90°,根据勾股定
理求出
所以矩形的面积是:
答案:5.如图,在梯形
ABCD中,AD∥BC,E为BC的中点,BC=
2AD,EA=ED=2,AC与ED相交于点F.
(1)求证:梯形ABCD是等腰梯形.
(2)当AB与AC具有什么位置关系时,四边形AECD是菱形?请说明理
由,并求出此时菱形AECD的面积.【解析】(1)如图,∵AD∥BC,∴∠1=∠DAE,∠2=∠3,
∵EA=ED,∴∠DAE=∠3,∴∠1=∠2.
又∵EB=EC,∴△AEB≌△DEC,
∴AB=DC,∴梯形ABCD是等腰梯形.(2)当AB⊥AC时,四边形AECD是菱形.理由如下:
∵AD∥BC,EB=EC=AD,
∴四边形ABED和四边形AECD都是平行四边形.
∴AB=DE.
∵AB⊥AC,EB=EC,∴AE=EB=EC.
∴四边形AECD是菱形.过点A作AG⊥BC于点G,
∵AE=EB=AB=2,∴△ABE为等边三角形.
∴∠1=60°,∴AG=AE·sin 60°=
∴S菱形AECD=EC×AG=
(1)平行四边形两组对边分别_____且_____;
(2)平行四边形两组对角分别_____;
(3)平行四边形对角线互相_____.平行相等相等平分2.矩形、菱形和正方形的性质.
(1)矩形的性质
①矩形的四个角都是_____;
②矩形的对角线_______________.
(2)菱形的性质
①菱形的四条边都_____;
②菱形的对角线互相_____,并且每条对角线_____一组对角.
(3)正方形具有_____与_____的所有性质.直角相等且互相平分相等垂直平分矩形菱形3.等腰梯形的性质.
(1)等腰梯形_______上的两个内角相等;
(2)等腰梯形的_______相等.同一底对角线【预习思考】
1.平行四边形的定义和性质在几何证明中的作用是什么?
提示:平行四边形的定义和性质是今后证明线段相等、两角相
等、两直线平行或垂直的重要依据.2.研究平行四边形的规律方法:
提示:在研究平行四边形所具有的特性(即性质)及平行四边形
的识别(即判定)时,应用数形结合、转化等数学思想,将其转化
为三角形问题,借助三角形的相关知识使平行四边形的性质和判
定得以展现. 平行四边形判定与性质的应用
【例1】如图,四边形ABCD中,AD∥BC,
AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形
ABCD是平行四边形.【解题探究】(1)试证明△ADE≌△CBF.
证明:∵AD∥BC,
∴∠ADB= ∠CBD.
∵AE⊥AD,CF⊥BC,
∴ ∠EAD = ∠FCB =90°.
∵AE=CF,∴△ADE≌△CBF,(2)AD和BC相等吗?
答:AD=BC.
(3)∵AD____BC,∴四边形ABCD是平行四边形. 【规律总结】
平行四边形的五种判定方法
1.两组对边分别平行的四边形是平行四边形;
2.两组对边分别相等的四边形是平行四边形;
3.一组对边平行且相等的四边形是平行四边形;
4.对角线互相平分的四边形是平行四边形;
5.两组对角分别相等的四边形是平行四边形.【跟踪训练】
1.如图,四边形ABCD
是平行四边形,点E在BC上.如果点F是
边AD上的点,那么△CDF与△ABE不一
定全等的条件是( )
(A)DF=BE (B)AF=CE
(C)CF=AE (D)CF∥AE【解析】选C.结合平行四边形性质,如果DF=BE,则与∠D=∠B,
CD=AB,恰好满足(S.A.S.)全等条件,即△CDF≌△ABE;如果
AF=CE,因为AD=CB,所以DF=BE,结合选项A,能够判断△CDF≌
△ABE;如果CF=AE,判断两三角形全等条件不具备;如果CF∥AE,
则四边形AECF是平行四边形,则有AF=CE,结合选项B,能够判断
△CDF≌△ABE.2.如图,在□ABCD中,
∠A=70°,将□ABCD折叠,使点D,C分
别落在点F,E处(点F,E都在AB所在的
直线上),折痕为MN,则∠AMF等于( )
(A)70° (B)40°
(C)30° (D)20°
【解析】选B.由□ABCD折叠得∠DMN=∠NMF=∠A=70°,
∴∠AMF=180°-70°-70°=40°. 殊平行四边形的性质与判定
【例2】如图,
在△ABC中,点O是AC边上(端点除外)
的一个动点,过点O作直线MN∥BC.
设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连结AE,
AF.那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
易错提醒:不要忘记把OA=OC作为已知条件运用!【规范解答】当点O运动到AC的中点(或OA=OC)时,
四边形AECF是矩形.………………………………………2分
理由如下:
∵CE平分∠BCA,∴∠1=∠2.
........................3分
又∵MN∥BC,∴∠1= ∠3 .
∴ ∠3 =∠2,∴ EO =CO………………………………………5分同理,FO=CO …………………………………………………6分
∴EO=FO.又OA=OC,
∴四边形AECF是平行四形……………………………………7分
又∵∠1=∠2,∠4=∠5,
∴∠1+∠5=∠2+∠4 …………………………………………8分
又∵∠1+∠5+∠2+∠4=180,
∴∠2+∠4=90°………………………………………………9分
∴四边形AECF是矩形…………………………………………10分【规律总结】
判定正方形常出现的三种错误
1.四条边相等就直接判定为正方形;
2.四个角为直角就判定为正方形;
3.对角线相等且垂直就判定为正方形.【跟踪训练】
3.已知菱形ABCD中,对角线AC与BD相交于点
O,∠BAD=120°,AC=4,则该菱形的面积是( )
(A) (B)16 (C) (D)8
【解析】选C. 因为∠BAD=120°,所以∠ABC=60°,所以菱形被
分成两个等边三角形,因为AC=4,故 所以BD=
面积4.点P是正方形ABCD
边AB上一点(不与A,B重合),连结PD并
将线段PD绕点P顺时针旋转90°,得线
段PE,连结BE,则∠CBE等于( )
(A)75° (B)60°
(C)45° (D)30°【解析】选C.延长AB,过E作AB的延长
线的垂线交于点F,由线段PD绕点P顺时
针旋转90°得线段PE,可知DP= EP ,
∠DPE=90°,所以∠EPF+∠DPA=
90°,而∠ADP+∠DPA=90°,所以∠EPF= ∠ADP.
又因为∠DAP=∠PFE=90°,所以△ADP≌△FPE,所以AP=FE,
AD=FP=AB,所以BF+PB=AP+PB,所以BF=AP,所以FE=BF,
所以∠EBF=∠BEF=45°,
所以∠CBE=90°-45°=45°. 等腰梯形的性质与判定
【例3】(6分)如图在等腰梯形ABCD中,AD∥BC,∠C=60°,AD=10,AB=18,求BC的长.【规范解答】
如图,过D点作DE∥AB交BC于E.
………………………………2分
∵AD∥BC,∴BE=AD=10,
DE=AB=DC=18,…………………………………………………4分
∵∠B=∠C=60°,∴EC=DC=DE=18,
∴BC=BE+EC=10+18=28.………………………………………6分【一题多解】方法一:如图,分别过A,D两点作AE⊥BC,DF⊥BC,垂足分别为E和F,
∵AD∥BC,AB=CD,
∴∠B=∠C=60°,EF=AD=10,∠BAE=∠CDF=30°,
∴Rt△ABE≌Rt△DCF,
∴BE=CF= AB=9,
∴BC=BE+EF+FC=9+10+9=28.方法二:如图,分别延长BA,CD交于点E.
∵AD∥BC,AB=CD,
∴∠B=∠C=60°,∠EAD=∠EDA,
∴△EBC与△EAD均为等边三角形,
∴BC=BE=AB+AE=AB+AD=18+10=28.方法三:如图,过点C作CE∥BA交AD的延长线于点E.
∵AD∥BC,∴四边形ABCE是平行四边形,
∠BCD=∠CDE=60°,又∠B=∠E=60°,
∴AB=EC=DC=18,
∴△DEC是等边三角形,∴DE=AB=18,
∴BC=AD+DE=10+18=28.【规律总结】
梯形常作辅助线“五种方法”
1.“平移腰”:把梯形分成一个平行四边形和一个三角形;
2.“作高”:使两腰在两个直角三角形中;
3.“平移对角线”:使两条对角线在同一个三角形中;
4.“延腰”:构造具有公共角的两个等腰三角形;
5.“等积变形”:连结梯形上底一端点和另一腰中点,并延长与下
底延长线交于一点,构成三角形.【跟踪训练】
5.如图,在梯形ABCD中,AB∥DC,AD=DC=CB,若
∠ABD=25°,则∠BAD的大小是( )
(A)40° (B)45°
(C)50° (D)60°
【解析】选C.由CB=DC,AB∥DC可得∠CBD=∠CDB=∠ABD=25°,得
到∠CBA=50°,由等腰梯形可得∠BAD=∠CBA=50°.6.如图,在平面直角
坐标系中,等腰梯形ABCD的下底在x轴
上,且B点坐标为(4,0),D点坐标为
(0,3),则AC长为( )
(A)4 (B)5 (C)6 (D)不能确定【解析】选B.如图,连结BD,
由题意得,OB=4,OD=3, 故可得BD=5.
又四边形ABCD是等腰梯形,
∴AC=BD=5.7.如图,等腰梯形ABCD
中,AD∥BC,点E是AD延长线上的一点,
且CE=CD,求证:∠B=∠E.
【证明】∵四边形ABCD为等腰梯形,AD∥BC,
∴∠B=∠BCD,∠BCD=∠CDE,∴∠B=∠CDE.
又∵CD=CE,∴∠CDE=∠E,∴∠B=∠E.1.如图,矩形ABCD的对角线AC,BD相
交于点O,CE∥BD,DE∥AC,若AC=4,
则四边形CODE的周长是( )
(A)4 (B)6 (C)8 (D)10
【解析】选C.∵CE∥BD,DE∥AC,∴四边形CODE为平行四边形.
又∵四边形ABCD为矩形,∴OD=OC=2,∴四边形CODE为菱形,其周
长为2×4=8.2.如图,菱形ABCD的周长是16,∠A=60°,则对
角线BD的长度为( )
(A)2 (B)
(C)4 (D)
【解析】选C.∵菱形ABCD的周长是16, ∴AB=BC=CD=DA=4,
∵∠A=60°,∴BD=AB=DA=4.3.如图,等腰梯形ABCD中,
AD∥BC,AB=AD=2,∠B=60°,则BC的长为_____.
【解析】作AE⊥BC,DF⊥BC,则EF=AD=2,
又∠B=60°,所以∠BAE=30°,
故BE= AB=1.同理,FC=1.
所以BC=BE+EF+FC=1+2+1=4.
答案:44.矩形ABCD的对角
线相交于点O,AB=4 cm,∠AOB=60°,
则矩形的面积为_____cm2.
【解析】根据矩形的性质得出AC=BD,OA= AC, OB= BD推出
OA=OB,得到等边三角形ABO,求出AC,由∠ABC=90°,根据勾股定
理求出
所以矩形的面积是:
答案:5.如图,在梯形
ABCD中,AD∥BC,E为BC的中点,BC=
2AD,EA=ED=2,AC与ED相交于点F.
(1)求证:梯形ABCD是等腰梯形.
(2)当AB与AC具有什么位置关系时,四边形AECD是菱形?请说明理
由,并求出此时菱形AECD的面积.【解析】(1)如图,∵AD∥BC,∴∠1=∠DAE,∠2=∠3,
∵EA=ED,∴∠DAE=∠3,∴∠1=∠2.
又∵EB=EC,∴△AEB≌△DEC,
∴AB=DC,∴梯形ABCD是等腰梯形.(2)当AB⊥AC时,四边形AECD是菱形.理由如下:
∵AD∥BC,EB=EC=AD,
∴四边形ABED和四边形AECD都是平行四边形.
∴AB=DE.
∵AB⊥AC,EB=EC,∴AE=EB=EC.
∴四边形AECD是菱形.过点A作AG⊥BC于点G,
∵AE=EB=AB=2,∴△ABE为等边三角形.
∴∠1=60°,∴AG=AE·sin 60°=
∴S菱形AECD=EC×AG=
