2020春华师版九下数学:几何的回顾复习课件(45张PPT)
文档属性
| 名称 | 2020春华师版九下数学:几何的回顾复习课件(45张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 963.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 18:31:12 | ||
图片预览










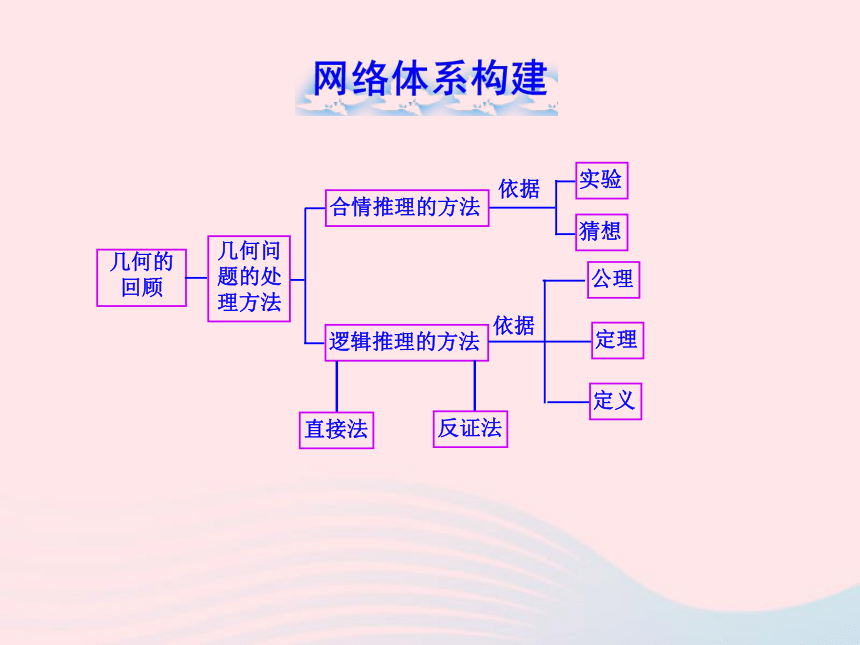

文档简介
课件45张PPT。 几何的回顾复习课一、反证法
1.在数学题目的求解中,当直接证明一个命题感到困难,甚至不
能证明时,我们可以采用反证法.所谓反证法,就是从否定结论
(作出相反判断) 出发,把相反的判断作为已知条件,在正确逻
辑的推理下,导出逻辑矛盾,得知相反判断是错误的,从而肯定
原命题的判断本身是正确的.2.反证法的证题步骤
(1) 反设:作出与求证的结论相反的假定.
(2) 归谬:由反设出发,推出了与公理、定义、定理或题设条件
相矛盾的结果.
(3) 结论:由于“矛盾”证明了反设不成立,从而肯定了原求证
结论正确.3.由于反证法的反设要十分准确,若命题结论的反面是多种情
形或比较隐晦时,就不太容易作出反设.现将常用的互为否定形
式的词语列表如下:4.初中阶段几种常使用反证法的情况
(1)基本定理或初始命题的证明
在数学中,许多基本定理是使用反证法来证明的.例如,
“经过直线外一点有且只有一条直线与已知直线平行”,“两
直线相交只有一个交点”等,因为在证明这种基本定理时,除
已经学过的公理及推论外,在此之前所导出的定理不多或者与
此命题相关的定理不多,所以常用反证法证明.(2)存在性问题的证明
在数学中,证明“存在”的问题很多,这种情况下,往往使用反
证法.如“同一条直线上的三点不能确定一个圆”.
应用反证法应注意的问题:
(1)必须正确否定结论.正确否定结论是应用反证法的前提.
(2)必须明确推理的特点.反证法所得到的矛盾一般是在相关领
域得到的,如平面几何中往往联系相关的公理、定义、定理等.
严格遵守推理规则,进行步步有据的严谨推理,导出矛盾证明
就结束了.二、三角形中的边角关系特点
1.三角形的性质
(1)三角形的稳定性:三角形的三边确定了,那么它的形状、
大小就都确定了,三角形的这个性质叫做三角形的稳定性.
(2)三角形三边之间的性质:三角形两边的和大于第三边,三
角形两边的差小于第三边.(3)与三角形的角有关的性质
①三角形内角和定理:三角形三个内角的和等于180°.
②三角形外角性质:
a.三角形的一个外角等于与它不相邻的两个内角的和.
b.三角形的一个外角大于与它不相邻的任一内角.
(4)三角形边角之间的关系:大边对大角,小边对小角,等边
对等角.注:1.应用三角形内角和定理的推论时,一定要理解其意思,
即“和它不相邻”的意义.
2.在计算角的度数、证明两个角相等或角的和差倍分时,常常
用到三角形内角和定理及推论1.
3.一般证明角不等时,应用“三角形的一个外角大于任何一个
和它不相邻的内角”来证明,所以需要找到三角形的外角.2.三角形三边关系的应用
其主要应用有:由三条线段的长,判断能否组成三角形;由三
角形两条边长的条件限制,求第三边;由三角形两条边长的条
件限制,求三角形的周长;三角形三边关系与代数知识结合应
用.
注:涉及等腰三角形的周长计算,易忽视分情况讨论问题或分
情况但是忽视了三角形三边关系的限制条件.依据 三角形的性质与判定
【相关链接】
在求角度的问题中,三角形内角和定理及外角的性质是两个常
用知识点.应用外角性质时,要弄清涉及的外角是哪一个三角
形的外角.角平分线、线段垂直平分线的性质是三角形的有关
计算以及三角形全等的证明中常用到的知识点,应灵活掌握.【例1】如图,点B,C,D,
F在同一直线上,已知AB=EC,AD=EF,BC=DF,
探索AB与EC的位置关系,并说明理由.
【思路点拨】【自主解答】AB与EC的位置关系是:AB∥EC.
理由:∵BC=DF,
∴BD=CF.
在△ABD和△ECF中
∴△ABD≌△ECF(S.S.S.),∴∠ABD=∠ECF,
∴AB∥EC. 等腰三角形
【相关链接】
(1)关于等腰三角形性质的问题,应清楚已知条件,若题目中
给出等腰三角形,则它的两个底角相等,还要注意“三线合一”
也可应用;若给出等边三角形,应清楚各边相等,每个角都等于60°,即把“等腰”或“等边”的条件转化为线段相等、角相等、线段与线段垂直以及角的度数相等.
(2)关于等腰三角形的判定问题,只要推出一个三角形中有两个角相等,则它们所对的边就相等,即“等角对等边”.【例2】如图,AB=AC,CD⊥AB
于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连结OA,BC,试判断直线OA,BC的关系并说明理由.
【思路点拨】(1)
(2)【自主解答】(1)在△ACD与△ABE中,
∵∠A=∠A,∠ADC=∠AEB=90°,AC=AB,
∴△ACD≌△ABE. ∴ AD=AE.
(2)互相垂直.理由如下:连结OA,BC,
在Rt△ADO与Rt△AEO中,
∵OA=OA,AD=AE,
∴Rt△ADO≌Rt△AEO.∴∠DAO=∠EAO,
即OA是∠BAC的平分线.
又∵AB=AC,∴ OA⊥BC. 特殊四边形的性质和判定
【相关链接】
(1)关于四边形的有关计算、证明题,要善于利用平行四边形、矩形、菱形、正方形以及梯形的性质和判定,也要与三角形全等、相似等知识点相结合,综合考查.
(2)在研究某些问题时,根据问题的特征,构造相应的特殊四边形,可使问题简单化.【例3】如图,
已知E是□ABCD中BC边的中点,连
结AE并延长AE交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)连结AC,BF,若∠AEC=2∠ABC,
求证:四边形ABFC为矩形.【思路点拨】
(1)
(2)【自主解答】(1)∵E是BC的中点,∴BE=CE.
∵四边形ABCD是平行四边形,
∴AB∥DF,∴∠BAE=∠CFE.
在△ABE与△FCE中
∴△ABE≌△FCE(A.A.S.).(2)∵∠AEC=∠ABE+∠BAE,
∠AEC=2∠ABC,
∴∠ABE=∠BAE,∴AE=BE.
∵△ABE≌△FCE,∴AE=EF,BE=CE,
∴AE=EF=BE=CE,且AF=BC,
∴四边形ABFC为矩形(对角线相等且平分的四边形是矩形). 反证法
【相关链接】
(1)用反证法证明有关问题时,结论的反面要正确、全面;反证法证明问题的关键是每一步都要有理有据,难点是导出矛盾,
可能与已知矛盾,也可能与某个定义、公理、定理矛盾.
(2)遇到下面形式的命题时,可借助反证法证明:①关于否定性结论的命题;②关于唯一性结论的命题;③关于“至多”“至
少”类结论的命题;④难以直接使用已知条件推出结论的命题.【例4】证明:圆的切线一定垂直于过切点的半径.
【思路点拨】
【自主解答】已知:直线l与⊙O相切于点A.
求证:l⊥OA.证明:如图,设圆O的一条半径是OA,直线l与圆切于A.假设直
线l不垂直于OA,过O作OM垂直l于点M,根据“垂线段最短”的
性质,有OA>OM,这就是说圆心到直线l的距离小于圆半径,于是
直线l与圆相交,这与l是圆的切线相矛盾.因此l⊥OA,即圆的
切线一定垂直于过切点的半径.【命题揭秘】
综合近几年中考发现三角形与四边形是必考内容,往往与
其他数学知识综合考查.同一个三角形中各个元素之间的关系
(边之间的关系、角之间的关系、边与角之间的关系),以及有
关的重要线段(高线、中线、角平分线、中位线)是考查重点,
同时注重考查两个三角形的全等关系(性质与判定);四边形是
平面几何研究的主要对象,四边形的知识是平行线和三角形知识的应用和深化.考查特殊四边形的性质和判定,注重灵活运
用;考查探究与推理,注重联系与综合.题型包含选择题、填空
题及解答题. 1.如图,在△ABC中,
∠C=70°,沿图中虚线截去∠C,则
∠1+∠2=( )
(A)360° (B)250° (C)180° (D)140°
【解析】选B.如图,∵∠1,∠2是△CDE的外角,
∴∠1=∠4+∠C,∠2=∠3+∠C,
即∠1+∠2=∠C+(∠C+∠3+∠4)
=70°+180°=250°.2.如图,在△ABC中,AB=
20 cm ,AC=12 cm,点P从点B出发以每秒
3 cm的速度向点A运动,点Q从点A同时出
发以每秒2 cm的速度向点C运动,其中一个动点到达端点时,另一
个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是
( )
(A)2.5秒 (B)3秒 (C)3.5秒 (D)4秒【解析】选D.由题可知BP=3t,AP=20-3t,AQ=2t,CQ=12-2t,当
△APQ是等腰三角形时,AP=AQ(当AP=PQ,AQ=PQ时,无法求解),
所以20-3t=2t,解得t=4,即运动时间为4秒.3.在等腰△ABC中,∠A=30°,AB=8,则AB边上
的高CD的长是________.
【解析】当等腰三角形ABC是锐角三角形,∠A为顶角时,∴CD=4;
当等腰三角形ABC是钝角三角形,∠A为底角,∠B为顶角时,
当等腰三角形ABC是钝角三角形,∠A为底角,∠C为顶
角时,
答案:4.将矩形纸片ABCD,按如图所示的方式折叠,
点A,点C恰好落在对角线BD上,得到菱形BEDF,若BC=6,则AB的长
为_______.【解析】设AB的长为x,
由题意知DC=x,BD=2x,
在Rt△BCD中,根据勾股定理得BC2+CD2=BD2,
∴62+x2=(2x)2.
解之得
答案:5.如图,在平行四边形
ABCD中,AD=10 cm,CD=6cm,E为AD上一
点,且BE=BC,CE=CD,则DE=________cm.
【解析】过点E作EM⊥BC于M点,点C作CN⊥DE于N点,则CM=EN
=DN,在三角形BEC中,设CM=a,根据勾股定理,得62-a2
=102-(10-a)2,解得a=1.8,所以DE=2a=3.6.
答案:3.66.用反证法证明:两条直线被第三条直线所截.如果同旁内角不
互补,那么这两条直线不平行.
已知:直线l1,l2被l3所截,
∠1+∠2≠180°.
求证:l1与l2不平行.
证明:假设l1 ____l2,则∠1+∠2 ____180°(两直线平行,同旁
内角互补),
这与∠1+∠2 ____180°矛盾,故____不成立.所以____.【解析】假设l1∥l2,则∠1+∠2=180°(两直线平行,同旁内角
互补),这与∠1+∠2≠180°矛盾,故假设不成立.所以结论成
立,l1与l2不平行.
答案:∥ = ≠ 假设 l1与l2不平行7.如图所示,在梯形ABCD中,AD∥BC,
∠BDC=90°,E为BC上一点,∠BDE=∠DBC.
(1)求证:DE=EC;
(2)若AD= BC,试判断四边形ABED的形状,并说明理由.【解析】(1)∵∠BDC=90°,∴∠BDE+∠EDC=90°,且
∠DBC+∠C=90°.
又∵∠BDE=∠DBC,∴∠EDC=∠C,∴DE=EC.
(2)四边形ABED为菱形.
∵∠BDE=∠DBC,∴BE=DE.
∵DE=EC,∴BE=EC= BC.
∵AD= BC,∴AD=BE.
又∵AD∥BC,∴四边形ABED为平行四边形.
又∵BE=DE,∴四边形ABED为菱形.8.如图,在正方形ABCD中,对角线AC,BD相交
于点O,E,F分别在OD,OC上,且DE=CF,连结DF,AE,AE的延长线交
DF于点M.
求证:AM⊥DF.【解析】在正方形ABCD中,AO=DO=OC,AC⊥BD,
∴∠AOE=∠DOF=90°,∠OAE+∠AEO=90°.
又∵DE=CF,∴OE=OF,∴△AOE≌△DOF,
∴∠AEO=∠DFO,∴∠OAE+∠DFO=90°,
∴∠AMF=90°,∴AM⊥DF.9.(1)如图①,□ABCD的对角线AC,BD交于点
O.直线EF过点O,分别交AD,BC于点E,F.
求证:AE=CF.(2)如图②,将□ABCD(纸片)沿过对角线交点O的直线EF折叠,点A
落在点A1处,点B落在点B1处.设FB1交CD于点G,A1B1分别交CD,DE
于点H,I.
求证:EI=FG.【解析】(1)∵AD∥BC,∴∠1=∠2,∠3=∠4.
∵OA=OC,∴△AOE≌△COF,∴AE=CF.(2)方法一:由(1)得AE=CF.
∵AE=A1E,∴A1E=CF.
∵∠A1=∠A=∠C,∠B1=∠B=∠D,
∠1=∠2,∴∠3=∠4,∴∠5=∠6.
在△A1IE与△CGF中,
∠A1=∠C,∠5=∠6,A1E=CF,∴△A1IE≌△CGF,∴EI=FG.方法二:∵A1E∥B1F,∴∠A1EI+
∠7+∠8=180°,同理,∠CFG+
∠7+∠8=180°,∴∠A1EI=∠CFG.
由(1)得AE=CF,∵AE=A1E,
∴A1E=CF.在△A1IE与△CGF中,
1.在数学题目的求解中,当直接证明一个命题感到困难,甚至不
能证明时,我们可以采用反证法.所谓反证法,就是从否定结论
(作出相反判断) 出发,把相反的判断作为已知条件,在正确逻
辑的推理下,导出逻辑矛盾,得知相反判断是错误的,从而肯定
原命题的判断本身是正确的.2.反证法的证题步骤
(1) 反设:作出与求证的结论相反的假定.
(2) 归谬:由反设出发,推出了与公理、定义、定理或题设条件
相矛盾的结果.
(3) 结论:由于“矛盾”证明了反设不成立,从而肯定了原求证
结论正确.3.由于反证法的反设要十分准确,若命题结论的反面是多种情
形或比较隐晦时,就不太容易作出反设.现将常用的互为否定形
式的词语列表如下:4.初中阶段几种常使用反证法的情况
(1)基本定理或初始命题的证明
在数学中,许多基本定理是使用反证法来证明的.例如,
“经过直线外一点有且只有一条直线与已知直线平行”,“两
直线相交只有一个交点”等,因为在证明这种基本定理时,除
已经学过的公理及推论外,在此之前所导出的定理不多或者与
此命题相关的定理不多,所以常用反证法证明.(2)存在性问题的证明
在数学中,证明“存在”的问题很多,这种情况下,往往使用反
证法.如“同一条直线上的三点不能确定一个圆”.
应用反证法应注意的问题:
(1)必须正确否定结论.正确否定结论是应用反证法的前提.
(2)必须明确推理的特点.反证法所得到的矛盾一般是在相关领
域得到的,如平面几何中往往联系相关的公理、定义、定理等.
严格遵守推理规则,进行步步有据的严谨推理,导出矛盾证明
就结束了.二、三角形中的边角关系特点
1.三角形的性质
(1)三角形的稳定性:三角形的三边确定了,那么它的形状、
大小就都确定了,三角形的这个性质叫做三角形的稳定性.
(2)三角形三边之间的性质:三角形两边的和大于第三边,三
角形两边的差小于第三边.(3)与三角形的角有关的性质
①三角形内角和定理:三角形三个内角的和等于180°.
②三角形外角性质:
a.三角形的一个外角等于与它不相邻的两个内角的和.
b.三角形的一个外角大于与它不相邻的任一内角.
(4)三角形边角之间的关系:大边对大角,小边对小角,等边
对等角.注:1.应用三角形内角和定理的推论时,一定要理解其意思,
即“和它不相邻”的意义.
2.在计算角的度数、证明两个角相等或角的和差倍分时,常常
用到三角形内角和定理及推论1.
3.一般证明角不等时,应用“三角形的一个外角大于任何一个
和它不相邻的内角”来证明,所以需要找到三角形的外角.2.三角形三边关系的应用
其主要应用有:由三条线段的长,判断能否组成三角形;由三
角形两条边长的条件限制,求第三边;由三角形两条边长的条
件限制,求三角形的周长;三角形三边关系与代数知识结合应
用.
注:涉及等腰三角形的周长计算,易忽视分情况讨论问题或分
情况但是忽视了三角形三边关系的限制条件.依据 三角形的性质与判定
【相关链接】
在求角度的问题中,三角形内角和定理及外角的性质是两个常
用知识点.应用外角性质时,要弄清涉及的外角是哪一个三角
形的外角.角平分线、线段垂直平分线的性质是三角形的有关
计算以及三角形全等的证明中常用到的知识点,应灵活掌握.【例1】如图,点B,C,D,
F在同一直线上,已知AB=EC,AD=EF,BC=DF,
探索AB与EC的位置关系,并说明理由.
【思路点拨】【自主解答】AB与EC的位置关系是:AB∥EC.
理由:∵BC=DF,
∴BD=CF.
在△ABD和△ECF中
∴△ABD≌△ECF(S.S.S.),∴∠ABD=∠ECF,
∴AB∥EC. 等腰三角形
【相关链接】
(1)关于等腰三角形性质的问题,应清楚已知条件,若题目中
给出等腰三角形,则它的两个底角相等,还要注意“三线合一”
也可应用;若给出等边三角形,应清楚各边相等,每个角都等于60°,即把“等腰”或“等边”的条件转化为线段相等、角相等、线段与线段垂直以及角的度数相等.
(2)关于等腰三角形的判定问题,只要推出一个三角形中有两个角相等,则它们所对的边就相等,即“等角对等边”.【例2】如图,AB=AC,CD⊥AB
于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连结OA,BC,试判断直线OA,BC的关系并说明理由.
【思路点拨】(1)
(2)【自主解答】(1)在△ACD与△ABE中,
∵∠A=∠A,∠ADC=∠AEB=90°,AC=AB,
∴△ACD≌△ABE. ∴ AD=AE.
(2)互相垂直.理由如下:连结OA,BC,
在Rt△ADO与Rt△AEO中,
∵OA=OA,AD=AE,
∴Rt△ADO≌Rt△AEO.∴∠DAO=∠EAO,
即OA是∠BAC的平分线.
又∵AB=AC,∴ OA⊥BC. 特殊四边形的性质和判定
【相关链接】
(1)关于四边形的有关计算、证明题,要善于利用平行四边形、矩形、菱形、正方形以及梯形的性质和判定,也要与三角形全等、相似等知识点相结合,综合考查.
(2)在研究某些问题时,根据问题的特征,构造相应的特殊四边形,可使问题简单化.【例3】如图,
已知E是□ABCD中BC边的中点,连
结AE并延长AE交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)连结AC,BF,若∠AEC=2∠ABC,
求证:四边形ABFC为矩形.【思路点拨】
(1)
(2)【自主解答】(1)∵E是BC的中点,∴BE=CE.
∵四边形ABCD是平行四边形,
∴AB∥DF,∴∠BAE=∠CFE.
在△ABE与△FCE中
∴△ABE≌△FCE(A.A.S.).(2)∵∠AEC=∠ABE+∠BAE,
∠AEC=2∠ABC,
∴∠ABE=∠BAE,∴AE=BE.
∵△ABE≌△FCE,∴AE=EF,BE=CE,
∴AE=EF=BE=CE,且AF=BC,
∴四边形ABFC为矩形(对角线相等且平分的四边形是矩形). 反证法
【相关链接】
(1)用反证法证明有关问题时,结论的反面要正确、全面;反证法证明问题的关键是每一步都要有理有据,难点是导出矛盾,
可能与已知矛盾,也可能与某个定义、公理、定理矛盾.
(2)遇到下面形式的命题时,可借助反证法证明:①关于否定性结论的命题;②关于唯一性结论的命题;③关于“至多”“至
少”类结论的命题;④难以直接使用已知条件推出结论的命题.【例4】证明:圆的切线一定垂直于过切点的半径.
【思路点拨】
【自主解答】已知:直线l与⊙O相切于点A.
求证:l⊥OA.证明:如图,设圆O的一条半径是OA,直线l与圆切于A.假设直
线l不垂直于OA,过O作OM垂直l于点M,根据“垂线段最短”的
性质,有OA>OM,这就是说圆心到直线l的距离小于圆半径,于是
直线l与圆相交,这与l是圆的切线相矛盾.因此l⊥OA,即圆的
切线一定垂直于过切点的半径.【命题揭秘】
综合近几年中考发现三角形与四边形是必考内容,往往与
其他数学知识综合考查.同一个三角形中各个元素之间的关系
(边之间的关系、角之间的关系、边与角之间的关系),以及有
关的重要线段(高线、中线、角平分线、中位线)是考查重点,
同时注重考查两个三角形的全等关系(性质与判定);四边形是
平面几何研究的主要对象,四边形的知识是平行线和三角形知识的应用和深化.考查特殊四边形的性质和判定,注重灵活运
用;考查探究与推理,注重联系与综合.题型包含选择题、填空
题及解答题. 1.如图,在△ABC中,
∠C=70°,沿图中虚线截去∠C,则
∠1+∠2=( )
(A)360° (B)250° (C)180° (D)140°
【解析】选B.如图,∵∠1,∠2是△CDE的外角,
∴∠1=∠4+∠C,∠2=∠3+∠C,
即∠1+∠2=∠C+(∠C+∠3+∠4)
=70°+180°=250°.2.如图,在△ABC中,AB=
20 cm ,AC=12 cm,点P从点B出发以每秒
3 cm的速度向点A运动,点Q从点A同时出
发以每秒2 cm的速度向点C运动,其中一个动点到达端点时,另一
个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是
( )
(A)2.5秒 (B)3秒 (C)3.5秒 (D)4秒【解析】选D.由题可知BP=3t,AP=20-3t,AQ=2t,CQ=12-2t,当
△APQ是等腰三角形时,AP=AQ(当AP=PQ,AQ=PQ时,无法求解),
所以20-3t=2t,解得t=4,即运动时间为4秒.3.在等腰△ABC中,∠A=30°,AB=8,则AB边上
的高CD的长是________.
【解析】当等腰三角形ABC是锐角三角形,∠A为顶角时,∴CD=4;
当等腰三角形ABC是钝角三角形,∠A为底角,∠B为顶角时,
当等腰三角形ABC是钝角三角形,∠A为底角,∠C为顶
角时,
答案:4.将矩形纸片ABCD,按如图所示的方式折叠,
点A,点C恰好落在对角线BD上,得到菱形BEDF,若BC=6,则AB的长
为_______.【解析】设AB的长为x,
由题意知DC=x,BD=2x,
在Rt△BCD中,根据勾股定理得BC2+CD2=BD2,
∴62+x2=(2x)2.
解之得
答案:5.如图,在平行四边形
ABCD中,AD=10 cm,CD=6cm,E为AD上一
点,且BE=BC,CE=CD,则DE=________cm.
【解析】过点E作EM⊥BC于M点,点C作CN⊥DE于N点,则CM=EN
=DN,在三角形BEC中,设CM=a,根据勾股定理,得62-a2
=102-(10-a)2,解得a=1.8,所以DE=2a=3.6.
答案:3.66.用反证法证明:两条直线被第三条直线所截.如果同旁内角不
互补,那么这两条直线不平行.
已知:直线l1,l2被l3所截,
∠1+∠2≠180°.
求证:l1与l2不平行.
证明:假设l1 ____l2,则∠1+∠2 ____180°(两直线平行,同旁
内角互补),
这与∠1+∠2 ____180°矛盾,故____不成立.所以____.【解析】假设l1∥l2,则∠1+∠2=180°(两直线平行,同旁内角
互补),这与∠1+∠2≠180°矛盾,故假设不成立.所以结论成
立,l1与l2不平行.
答案:∥ = ≠ 假设 l1与l2不平行7.如图所示,在梯形ABCD中,AD∥BC,
∠BDC=90°,E为BC上一点,∠BDE=∠DBC.
(1)求证:DE=EC;
(2)若AD= BC,试判断四边形ABED的形状,并说明理由.【解析】(1)∵∠BDC=90°,∴∠BDE+∠EDC=90°,且
∠DBC+∠C=90°.
又∵∠BDE=∠DBC,∴∠EDC=∠C,∴DE=EC.
(2)四边形ABED为菱形.
∵∠BDE=∠DBC,∴BE=DE.
∵DE=EC,∴BE=EC= BC.
∵AD= BC,∴AD=BE.
又∵AD∥BC,∴四边形ABED为平行四边形.
又∵BE=DE,∴四边形ABED为菱形.8.如图,在正方形ABCD中,对角线AC,BD相交
于点O,E,F分别在OD,OC上,且DE=CF,连结DF,AE,AE的延长线交
DF于点M.
求证:AM⊥DF.【解析】在正方形ABCD中,AO=DO=OC,AC⊥BD,
∴∠AOE=∠DOF=90°,∠OAE+∠AEO=90°.
又∵DE=CF,∴OE=OF,∴△AOE≌△DOF,
∴∠AEO=∠DFO,∴∠OAE+∠DFO=90°,
∴∠AMF=90°,∴AM⊥DF.9.(1)如图①,□ABCD的对角线AC,BD交于点
O.直线EF过点O,分别交AD,BC于点E,F.
求证:AE=CF.(2)如图②,将□ABCD(纸片)沿过对角线交点O的直线EF折叠,点A
落在点A1处,点B落在点B1处.设FB1交CD于点G,A1B1分别交CD,DE
于点H,I.
求证:EI=FG.【解析】(1)∵AD∥BC,∴∠1=∠2,∠3=∠4.
∵OA=OC,∴△AOE≌△COF,∴AE=CF.(2)方法一:由(1)得AE=CF.
∵AE=A1E,∴A1E=CF.
∵∠A1=∠A=∠C,∠B1=∠B=∠D,
∠1=∠2,∴∠3=∠4,∴∠5=∠6.
在△A1IE与△CGF中,
∠A1=∠C,∠5=∠6,A1E=CF,∴△A1IE≌△CGF,∴EI=FG.方法二:∵A1E∥B1F,∴∠A1EI+
∠7+∠8=180°,同理,∠CFG+
∠7+∠8=180°,∴∠A1EI=∠CFG.
由(1)得AE=CF,∵AE=A1E,
∴A1E=CF.在△A1IE与△CGF中,
