北师大版九下数学2.3确定二次函数的表达式习题课件(26张)
文档属性
| 名称 | 北师大版九下数学2.3确定二次函数的表达式习题课件(26张) |  | |
| 格式 | zip | ||
| 文件大小 | 550.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 08:06:13 | ||
图片预览



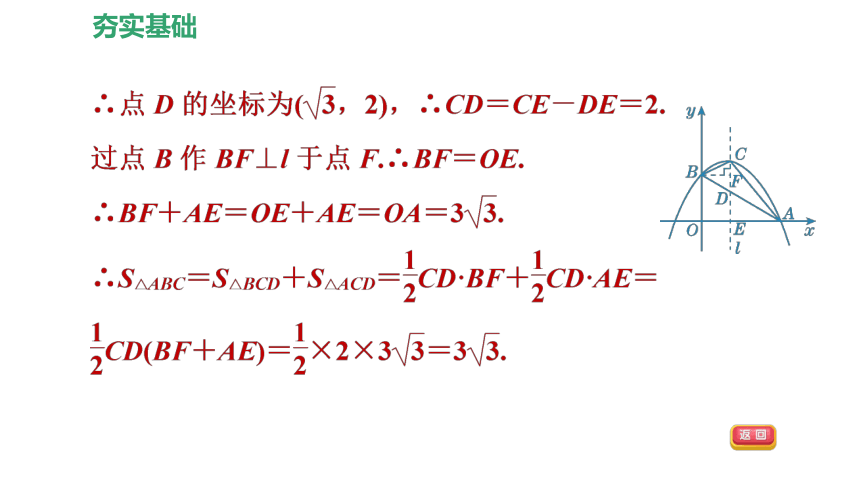



文档简介
(共26张PPT)
3 确定二次函数的表达式
第2章 二次函数
BS版 九年级下
提示:点击 进入习题
答案显示
习题链接
见习题
见习题
B
1
2
3
4
见习题
见习题
5
见习题
6
夯实基础
夯实基础
夯实基础
夯实基础
2.已知A(1,0),B(0,-1),C(-1,2),D(2,-1),E(4,2)五个点,抛物线y=a(x-1)2+k(a>0)经过其中三个点.
(1)求证:C,E两点不可能同时在抛物线y=a(x-1)2+k(a>0)上;
夯实基础
证明:由题意可知,抛物线的对称轴为直线x=1.
若点C(-1,2)在抛物线上,
夯实基础
则点C关于直线x=1的对称点(3,2)也在这条抛物线
上,此时点E(4,2)不在这条抛物线上.同理,若点E(4,2)在抛物线上,则点C(-1,2)不在抛物线上.∴C,E两点不可能同时在抛物线y=a(x-1)2+
k(a>0)上.
(2)点A在抛物线y=a(x-1)2+k(a>0)上吗?为什么?
夯实基础
解:点A不在抛物线上.
理由:若点A(1,0)在抛物线y=a(x-1)2+k(a>0)上,则k=0.∴y=a(x-1)2(a>0).
易知B(0,-1),D(2,-1)都不在抛物线上.
由(1)知C,E两点不可能同时在抛物线上,
∴与抛物线经过其中三个点矛盾.
∴点A不在抛物线上.
(3)求a和k的值.
夯实基础
夯实基础
夯实基础
3.【2019?烟台】已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
下列结论:①抛物线的开口向上;
②抛物线的对称轴为直线x=2;
③当0<x<4时,y>0;
x -1 0 2 3 4
y 5 0 -4 -3 0
夯实基础
④抛物线与x轴的两个交点间的距离是4;
⑤若A(x1,2),B(x2,3)是抛物线上两点,则x1<x2.
其中正确的个数是( )
A.2 B.3 C.4 D.5
B
4.在平面直角坐标系中,设二次函数为y=(x+a)
(x-a-1),其中a≠0.
(1)若此二次函数的图象经过点(1,-2),求该二次函数的表达式;
夯实基础
解:由二次函数的图象经过点(1,-2),
得(a+1)(-a)=-2,解得a1=-2,a2=1.
当a=-2时,二次函数的表达式为y=(x-2)(x+2-1),
即y=x2-x-2;
(2)若一次函数y=ax+b的图象与二次函数的图象经过x轴上同一点,探究实数a,b满足的关系式;
夯实基础
当a=1时,二次函数的表达式为y=(x+1)(x-2),
即y=x2-x-2.
综上所述,该二次函数的表达式为y=x2-x-2.
解:当y=0时,(x+a)(x-a-1)=0,
解得x=-a或x=a+1,
夯实基础
所以二次函数的图象与x轴的交点是(-a,0),
(a+1,0).
当y=ax+b的图象经过(-a,0)时,
-a2+b=0,即b=a2;
当y=ax+b的图象经过(a+1,0)时,
a2+a+b=0,即b=-a2-a.
(3)已知点P(x0,m)和Q(1,n)在二次函数的图象上,若m<n,求x0的取值范围.
夯实基础
夯实基础
5.【2018?苏州】如图,已知抛物线y=x2-4与x轴交于点A,B(点A位于点B的左侧),C为顶点,直线y=x+m经过点A,与y轴交于点D.
(1)求线段AD的长;
整合方法
(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为C′,若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.
整合方法
整合方法
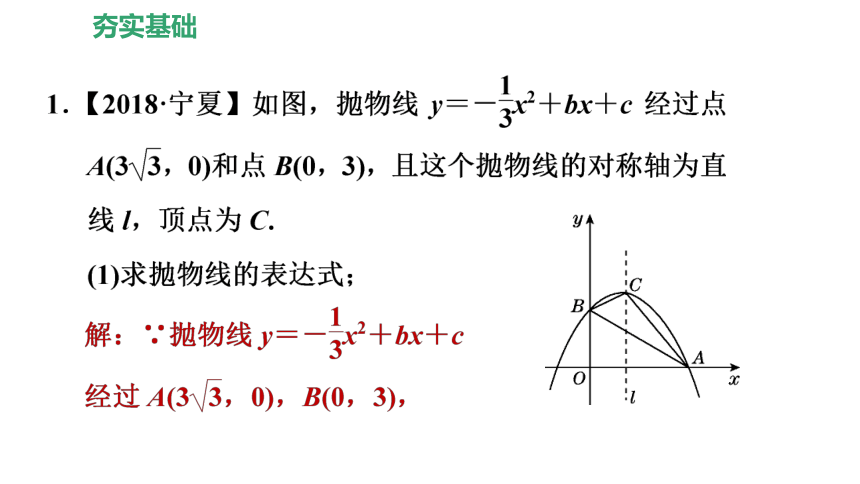
6.【中考?菏泽】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.
(1)试求抛物线的函数表达式;
整合方法
(2)记抛物线的顶点为D,求△BCD的面积;
整合方法
整合方法
整合方法
整合方法
3 确定二次函数的表达式
第2章 二次函数
BS版 九年级下
提示:点击 进入习题
答案显示
习题链接
见习题
见习题
B
1
2
3
4
见习题
见习题
5
见习题
6
夯实基础
夯实基础
夯实基础
夯实基础
2.已知A(1,0),B(0,-1),C(-1,2),D(2,-1),E(4,2)五个点,抛物线y=a(x-1)2+k(a>0)经过其中三个点.
(1)求证:C,E两点不可能同时在抛物线y=a(x-1)2+k(a>0)上;
夯实基础
证明:由题意可知,抛物线的对称轴为直线x=1.
若点C(-1,2)在抛物线上,
夯实基础
则点C关于直线x=1的对称点(3,2)也在这条抛物线
上,此时点E(4,2)不在这条抛物线上.同理,若点E(4,2)在抛物线上,则点C(-1,2)不在抛物线上.∴C,E两点不可能同时在抛物线y=a(x-1)2+
k(a>0)上.
(2)点A在抛物线y=a(x-1)2+k(a>0)上吗?为什么?
夯实基础
解:点A不在抛物线上.
理由:若点A(1,0)在抛物线y=a(x-1)2+k(a>0)上,则k=0.∴y=a(x-1)2(a>0).
易知B(0,-1),D(2,-1)都不在抛物线上.
由(1)知C,E两点不可能同时在抛物线上,
∴与抛物线经过其中三个点矛盾.
∴点A不在抛物线上.
(3)求a和k的值.
夯实基础
夯实基础
夯实基础
3.【2019?烟台】已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
下列结论:①抛物线的开口向上;
②抛物线的对称轴为直线x=2;
③当0<x<4时,y>0;
x -1 0 2 3 4
y 5 0 -4 -3 0
夯实基础
④抛物线与x轴的两个交点间的距离是4;
⑤若A(x1,2),B(x2,3)是抛物线上两点,则x1<x2.
其中正确的个数是( )
A.2 B.3 C.4 D.5
B
4.在平面直角坐标系中,设二次函数为y=(x+a)
(x-a-1),其中a≠0.
(1)若此二次函数的图象经过点(1,-2),求该二次函数的表达式;
夯实基础
解:由二次函数的图象经过点(1,-2),
得(a+1)(-a)=-2,解得a1=-2,a2=1.
当a=-2时,二次函数的表达式为y=(x-2)(x+2-1),
即y=x2-x-2;
(2)若一次函数y=ax+b的图象与二次函数的图象经过x轴上同一点,探究实数a,b满足的关系式;
夯实基础
当a=1时,二次函数的表达式为y=(x+1)(x-2),
即y=x2-x-2.
综上所述,该二次函数的表达式为y=x2-x-2.
解:当y=0时,(x+a)(x-a-1)=0,
解得x=-a或x=a+1,
夯实基础
所以二次函数的图象与x轴的交点是(-a,0),
(a+1,0).
当y=ax+b的图象经过(-a,0)时,
-a2+b=0,即b=a2;
当y=ax+b的图象经过(a+1,0)时,
a2+a+b=0,即b=-a2-a.
(3)已知点P(x0,m)和Q(1,n)在二次函数的图象上,若m<n,求x0的取值范围.
夯实基础
夯实基础
5.【2018?苏州】如图,已知抛物线y=x2-4与x轴交于点A,B(点A位于点B的左侧),C为顶点,直线y=x+m经过点A,与y轴交于点D.
(1)求线段AD的长;
整合方法
(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为C′,若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.
整合方法
整合方法
6.【中考?菏泽】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.
(1)试求抛物线的函数表达式;
整合方法
(2)记抛物线的顶点为D,求△BCD的面积;
整合方法
整合方法
整合方法
整合方法
