北师大版九下数学3.5确定圆的条件习题课件(31张)
文档属性
| 名称 | 北师大版九下数学3.5确定圆的条件习题课件(31张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 11:36:12 | ||
图片预览










文档简介
(共31张PPT)
5 确定圆的条件
第三章 圆
答案显示
C
B
C
B
B
5
B
C
B
答案显示
C
(1)见习题.(2)成立.理由略.
1.如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意三点,能画圆的个数是( )
A.1 B.2 C.3 D.4
C
【点拨】由不在同一条直线上的三点确定一个圆可知,过A,B,D三点、B,C,D三点、A,C,D三点可分别画一个圆,故选C.
2.已知AB=4 cm,则过点A,B且半径为3 cm的圆有( )
A.1个 B.2个 C.3个 D.4个
B
【点拨】过点A,B且半径为3 cm的圆的圆心应当在线段AB的垂直平分线上,且到A,B两点的距离为3 cm,这样的圆心有2个,故选B.
3.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P B.点Q C.点R D.点M
B
4.下列关于确定一个圆的说法中,正确的是( )
A.三个点一定能确定一个圆
B.以已知线段为半径能确定一个圆
C.以已知线段为直径能确定一个圆
D.菱形的四个顶点能确定一个圆
C
5.如图,点A,B,C均在6×6的正方形网格格点上,过A,B,C三点的圆除经过A,B,C三点外还能经过的格点数为________.
5
【点拨】如图,连接AB,分别作AB,AC的中垂线,两直线的交点为O,以O为圆心、OA为半径作圆,则⊙O即为过A,B,C三点的圆,由图可知,⊙O还经过点D,E,F,G,H这5个格点,故答案为5.
6.下列说法中,真命题的个数是( )
①任何三角形有且只有一个外接圆;
②任何圆有且只有一个内接三角形;
③三角形的外心不一定在三角形内;
④三角形的外心到三角形三边的距离相等;
⑤三点确定一个圆.
A.1 B.2 C.3 D.4
B
【点拨】 ①③是真命题.
7.【中考·河北】如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
A.△ABE B.△ACF C.△ABD D.△ADE
B
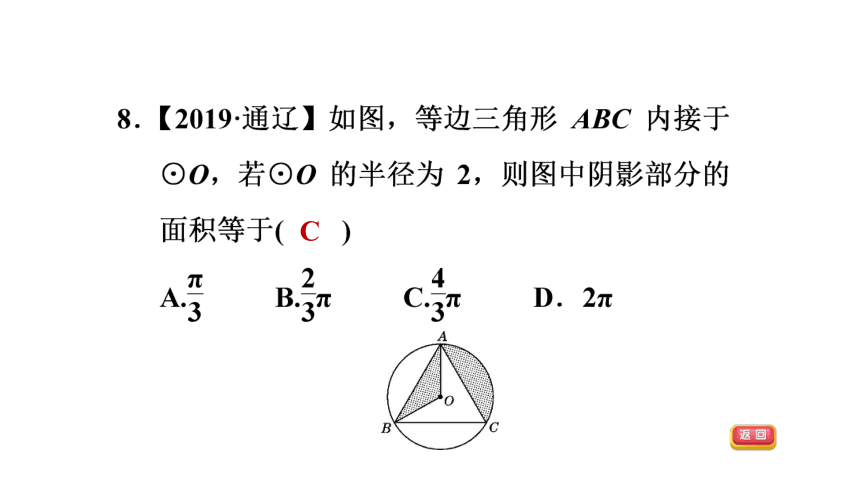
C
【答案】 B
10.【2019·广元】如图,△ABC是⊙O的内接三角形,且AB是⊙O的直径,点P为⊙O上的动点,且∠BPC=60°,⊙O的半径为6,则点P到AC距离的最大值是________.
【答案】 C
13.【2018·南京】如图,在四边形ABCD中,BC=CD,∠C=2∠BAD,O是四边形ABCD内一点,且OA=OB=OD.
求证:(1)∠BOD=∠C;
证明:∵OA=OB=OD,∴点A,B,D在以点O为圆心,OA为半径的圆上,∴∠BOD=2∠BAD,
又∵∠C=2∠BAD,∴∠BOD=∠C.
(2)四边形OBCD是菱形.
证明:如图,连接AD.弧AC所对的圆周角∠ABC=∠ADC,弧CD所对的圆周角∠DBC=∠DAC.
∵四边形BDCE是菱形,∴∠ABC=∠DBC.∴∠ADC=∠DAC,∴AC=CD.又∵CD=CE,∴AC=CE.
证明:如图,作CH⊥AE于H.
∵AC=CE,∴H为AE的中点,即AH=EH.
在Rt△CHB中,BC2-CH2=BH2;
在Rt△AHC中,AC2-CH2=AH2.
∴BC2-AC2=BH2-AH2=(BH+AH)(BH-AH)=AB·BE.∵BE=CE,∴BE=AC.∴BC2-AC2=AB·AC.
15.已知⊙O是等边三角形ABC的外接圆.
(1)如图①,若PC为⊙O的直径,连接AP,BP,
求证:AP+BP=PC.
(2)如图②,若点P是弧AB上任意一点,连接AP,BP,CP,那么结论AP+BP=PC还成立吗?请说明理由.
5 确定圆的条件
第三章 圆
答案显示
C
B
C
B
B
5
B
C
B
答案显示
C
(1)见习题.(2)成立.理由略.
1.如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意三点,能画圆的个数是( )
A.1 B.2 C.3 D.4
C
【点拨】由不在同一条直线上的三点确定一个圆可知,过A,B,D三点、B,C,D三点、A,C,D三点可分别画一个圆,故选C.
2.已知AB=4 cm,则过点A,B且半径为3 cm的圆有( )
A.1个 B.2个 C.3个 D.4个
B
【点拨】过点A,B且半径为3 cm的圆的圆心应当在线段AB的垂直平分线上,且到A,B两点的距离为3 cm,这样的圆心有2个,故选B.
3.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P B.点Q C.点R D.点M
B
4.下列关于确定一个圆的说法中,正确的是( )
A.三个点一定能确定一个圆
B.以已知线段为半径能确定一个圆
C.以已知线段为直径能确定一个圆
D.菱形的四个顶点能确定一个圆
C
5.如图,点A,B,C均在6×6的正方形网格格点上,过A,B,C三点的圆除经过A,B,C三点外还能经过的格点数为________.
5
【点拨】如图,连接AB,分别作AB,AC的中垂线,两直线的交点为O,以O为圆心、OA为半径作圆,则⊙O即为过A,B,C三点的圆,由图可知,⊙O还经过点D,E,F,G,H这5个格点,故答案为5.
6.下列说法中,真命题的个数是( )
①任何三角形有且只有一个外接圆;
②任何圆有且只有一个内接三角形;
③三角形的外心不一定在三角形内;
④三角形的外心到三角形三边的距离相等;
⑤三点确定一个圆.
A.1 B.2 C.3 D.4
B
【点拨】 ①③是真命题.
7.【中考·河北】如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
A.△ABE B.△ACF C.△ABD D.△ADE
B
C
【答案】 B
10.【2019·广元】如图,△ABC是⊙O的内接三角形,且AB是⊙O的直径,点P为⊙O上的动点,且∠BPC=60°,⊙O的半径为6,则点P到AC距离的最大值是________.
【答案】 C
13.【2018·南京】如图,在四边形ABCD中,BC=CD,∠C=2∠BAD,O是四边形ABCD内一点,且OA=OB=OD.
求证:(1)∠BOD=∠C;
证明:∵OA=OB=OD,∴点A,B,D在以点O为圆心,OA为半径的圆上,∴∠BOD=2∠BAD,
又∵∠C=2∠BAD,∴∠BOD=∠C.
(2)四边形OBCD是菱形.
证明:如图,连接AD.弧AC所对的圆周角∠ABC=∠ADC,弧CD所对的圆周角∠DBC=∠DAC.
∵四边形BDCE是菱形,∴∠ABC=∠DBC.∴∠ADC=∠DAC,∴AC=CD.又∵CD=CE,∴AC=CE.
证明:如图,作CH⊥AE于H.
∵AC=CE,∴H为AE的中点,即AH=EH.
在Rt△CHB中,BC2-CH2=BH2;
在Rt△AHC中,AC2-CH2=AH2.
∴BC2-AC2=BH2-AH2=(BH+AH)(BH-AH)=AB·BE.∵BE=CE,∴BE=AC.∴BC2-AC2=AB·AC.
15.已知⊙O是等边三角形ABC的外接圆.
(1)如图①,若PC为⊙O的直径,连接AP,BP,
求证:AP+BP=PC.
(2)如图②,若点P是弧AB上任意一点,连接AP,BP,CP,那么结论AP+BP=PC还成立吗?请说明理由.
