北师大版九下数学3.7切线长定理习题课件(21张)
文档属性
| 名称 | 北师大版九下数学3.7切线长定理习题课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 707.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
人教版九年级上
7 切线长定理
第三章 圆
答案显示
B
D
C
C
D
A
D
A
答案显示
C
(1)AB+CD=BC+AD.(2)AB+CD<BC+AD.
(1)见习题.(2)相等.理由略.
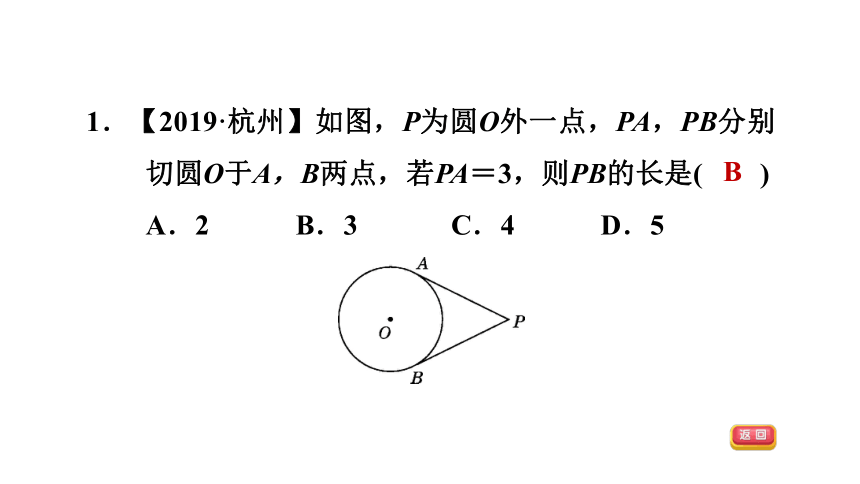
1.【2019·杭州】如图,P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=3,则PB的长是( )
A.2 B.3 C.4 D.5
B
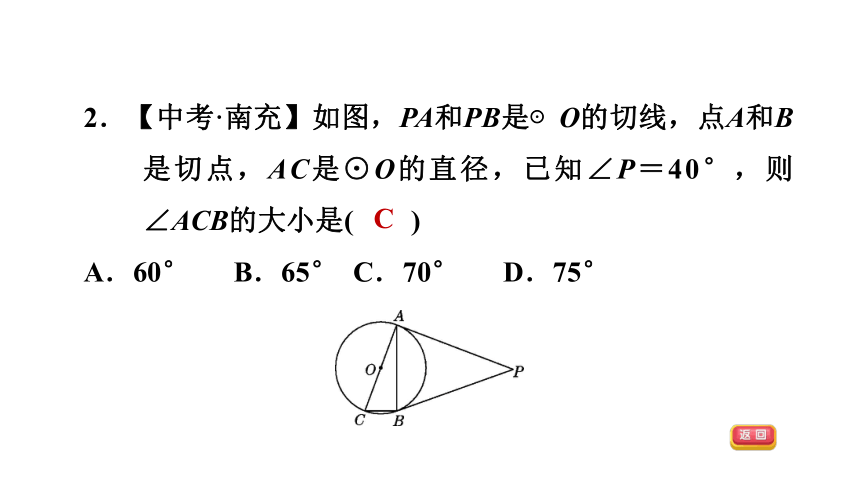
2.【中考·南充】如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.60° B.65° C.70° D.75°
C
3.【2019·益阳】如图,PA,PB为圆O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
A.PA=PB B.∠BPD=∠APD
C.AB⊥PD D.AB平分PD
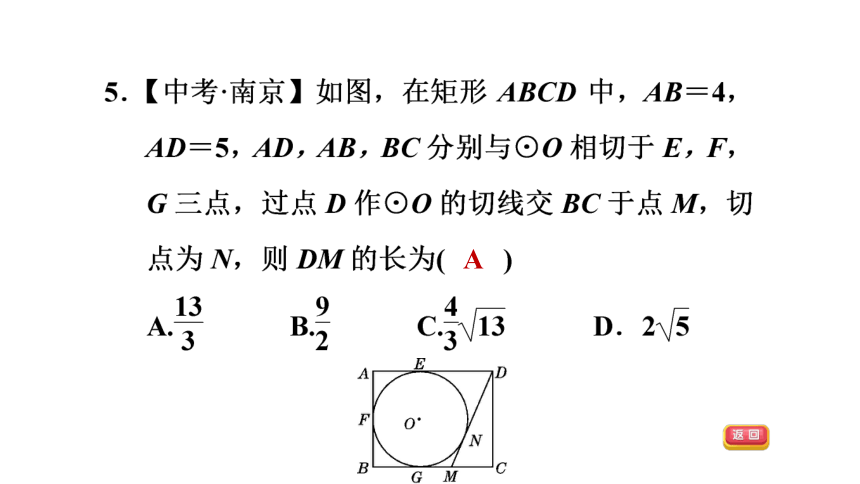
D
D
A
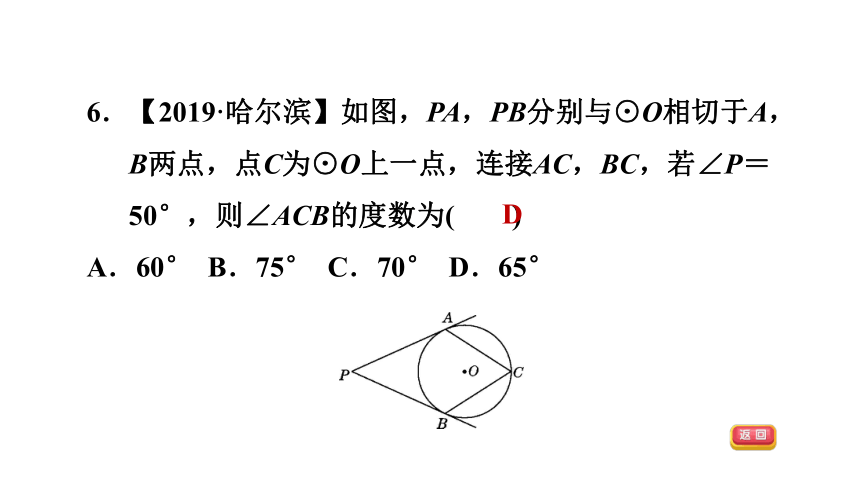
6.【2019·哈尔滨】如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连接AC,BC,若∠P=50°,则∠ACB的度数为( )
A.60° B.75° C.70° D.65°
D
C
A
9.既有外接圆,又有内切圆的平行四边形是( )
A.矩形 B.菱形
C.正方形 D.矩形或菱形
【点拨】解答本题的关键是(1)四边形的内切圆到四边形四条边的距离相等;(2)圆内接四边形对角互补.
C
10.【2019·枣庄】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
解:直线CD与⊙O相切.理由如下:连接OC.
∵CB=CD,CO=CO,OB=OD,∴△OCB≌△OCD(SSS).∴∠ODC=∠OBC=90°.∴OD⊥CD.∴直线CD与⊙O相切.
(2)若BE=2,DE=4,求⊙O的半径及AC的长.
11.【2019·资阳】如图,AC是⊙O的直径,PA切⊙O于点A,PB切⊙O于点B,且∠APB=60°.
(1)求∠BAC的度数;
解:∵PA切⊙O于点A,PB切⊙O于点B,
∴PA=PB,∠PAC=90°.
∵∠APB=60°,∴△APB是等边三角形,
∴∠BAP=60°,∴∠BAC=90°-∠BAP=30°.
(2)若PA=1,求点O到弦AB的距离.
12.【中考·威海】已知:AB为⊙O的直径,AB=2,弦DE=1,直线AD与BE相交于点C,弦DE在⊙O上运动且保持长度不变,⊙O的切线DF交BC于点F.
(1)如图①,若DE∥AB,求证:CF=EF.
证明:如图,连接OD,OE.
∵AB=2,∴OA=OD=OE=OB=1.∵DE=1,∴OD=OE=DE.∴△ODE是等边三角形.∴∠ODE=∠OED=60°.
∵DE∥AB,∴∠AOD=∠ODE=60°,∠EOB=∠OED=60°.∴△AOD和△BOE都是等边三角形.∴∠OAD=∠OBE=60°.
∵DE∥AB,∴∠CDE=∠OAD=60°,∠CED=∠OBE=60°.∴△CDE是等边三角形.
∵DF是⊙O的切线,∴OD⊥DF.∴∠EDF=90°-60°=30°.∴∠DFE=90°.∴DF⊥CE.∴CF=EF.
(2)如图②,当点E运动至与点B重合时,试判断CF与BF是否相等,并说明理由.
解:相等.理由:当点E运动至与点B重合时,
BC与⊙O只有一个公共点,即BC是⊙O的切线.
∵⊙O的切线DF交BC于点F,∴BF=DF.∴∠BDF=∠DBF.∵AB是⊙O的直径,∴∠ADB=∠BDC=90°.∴∠BDF+∠FDC=∠C+∠DBF=90°.
∴∠FDC=∠C.∴DF=CF.∴BF=CF.
13.(1)如图①,四边形ABCD是⊙O的外切四边形,切点分别为E,F,G,H,说明AB+CD与BC+AD的大小关系;
解:由切线长定理,得AE=AH,BE=BF,CF=CG,DG=DH,∴AB+CD=AE+BE+CG+DG=AH+BF+CF+DH=BC+AD,
即AB+CD=BC+AD.
(2)如图②,四边形ABCD的三边分别切⊙O于点F,G,H,说明AB+CD与BC+AD的大小关系.
解:过点B作⊙O的切线,交AD于点M.
由(1)可知BM+CD=BC+MD.
∵AB<AM+BM,∴AB+BM+CD<AM+BM+BC+MD,即AB+CD<BC+AD.
人教版九年级上
7 切线长定理
第三章 圆
答案显示
B
D
C
C
D
A
D
A
答案显示
C
(1)AB+CD=BC+AD.(2)AB+CD<BC+AD.
(1)见习题.(2)相等.理由略.
1.【2019·杭州】如图,P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=3,则PB的长是( )
A.2 B.3 C.4 D.5
B
2.【中考·南充】如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.60° B.65° C.70° D.75°
C
3.【2019·益阳】如图,PA,PB为圆O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
A.PA=PB B.∠BPD=∠APD
C.AB⊥PD D.AB平分PD
D
D
A
6.【2019·哈尔滨】如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连接AC,BC,若∠P=50°,则∠ACB的度数为( )
A.60° B.75° C.70° D.65°
D
C
A
9.既有外接圆,又有内切圆的平行四边形是( )
A.矩形 B.菱形
C.正方形 D.矩形或菱形
【点拨】解答本题的关键是(1)四边形的内切圆到四边形四条边的距离相等;(2)圆内接四边形对角互补.
C
10.【2019·枣庄】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
解:直线CD与⊙O相切.理由如下:连接OC.
∵CB=CD,CO=CO,OB=OD,∴△OCB≌△OCD(SSS).∴∠ODC=∠OBC=90°.∴OD⊥CD.∴直线CD与⊙O相切.
(2)若BE=2,DE=4,求⊙O的半径及AC的长.
11.【2019·资阳】如图,AC是⊙O的直径,PA切⊙O于点A,PB切⊙O于点B,且∠APB=60°.
(1)求∠BAC的度数;
解:∵PA切⊙O于点A,PB切⊙O于点B,
∴PA=PB,∠PAC=90°.
∵∠APB=60°,∴△APB是等边三角形,
∴∠BAP=60°,∴∠BAC=90°-∠BAP=30°.
(2)若PA=1,求点O到弦AB的距离.
12.【中考·威海】已知:AB为⊙O的直径,AB=2,弦DE=1,直线AD与BE相交于点C,弦DE在⊙O上运动且保持长度不变,⊙O的切线DF交BC于点F.
(1)如图①,若DE∥AB,求证:CF=EF.
证明:如图,连接OD,OE.
∵AB=2,∴OA=OD=OE=OB=1.∵DE=1,∴OD=OE=DE.∴△ODE是等边三角形.∴∠ODE=∠OED=60°.
∵DE∥AB,∴∠AOD=∠ODE=60°,∠EOB=∠OED=60°.∴△AOD和△BOE都是等边三角形.∴∠OAD=∠OBE=60°.
∵DE∥AB,∴∠CDE=∠OAD=60°,∠CED=∠OBE=60°.∴△CDE是等边三角形.
∵DF是⊙O的切线,∴OD⊥DF.∴∠EDF=90°-60°=30°.∴∠DFE=90°.∴DF⊥CE.∴CF=EF.
(2)如图②,当点E运动至与点B重合时,试判断CF与BF是否相等,并说明理由.
解:相等.理由:当点E运动至与点B重合时,
BC与⊙O只有一个公共点,即BC是⊙O的切线.
∵⊙O的切线DF交BC于点F,∴BF=DF.∴∠BDF=∠DBF.∵AB是⊙O的直径,∴∠ADB=∠BDC=90°.∴∠BDF+∠FDC=∠C+∠DBF=90°.
∴∠FDC=∠C.∴DF=CF.∴BF=CF.
13.(1)如图①,四边形ABCD是⊙O的外切四边形,切点分别为E,F,G,H,说明AB+CD与BC+AD的大小关系;
解:由切线长定理,得AE=AH,BE=BF,CF=CG,DG=DH,∴AB+CD=AE+BE+CG+DG=AH+BF+CF+DH=BC+AD,
即AB+CD=BC+AD.
(2)如图②,四边形ABCD的三边分别切⊙O于点F,G,H,说明AB+CD与BC+AD的大小关系.
解:过点B作⊙O的切线,交AD于点M.
由(1)可知BM+CD=BC+MD.
∵AB<AM+BM,∴AB+BM+CD<AM+BM+BC+MD,即AB+CD<BC+AD.
