北师大版九下数学3.8圆内接正多边形习题课件(25张)
文档属性
| 名称 | 北师大版九下数学3.8圆内接正多边形习题课件(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 11:38:22 | ||
图片预览






文档简介
(共25张PPT)
人教版九年级上
8 圆内接正多边形
第三章 圆
答案显示
B
B
C
C
A
D
C
答案显示
图略.
见习题.
A
(1)30°;(2)9.6.
1.正多边形的中心角与该正多边形的一个内角的关系为( )
A.两角互余 B.两角互补
C.两角互余或互补 D.不能确定
B
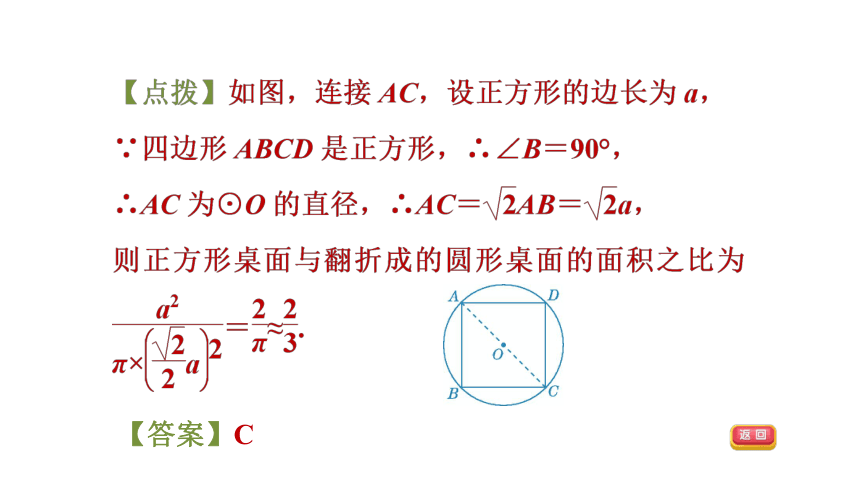
【答案】C
B
D
C
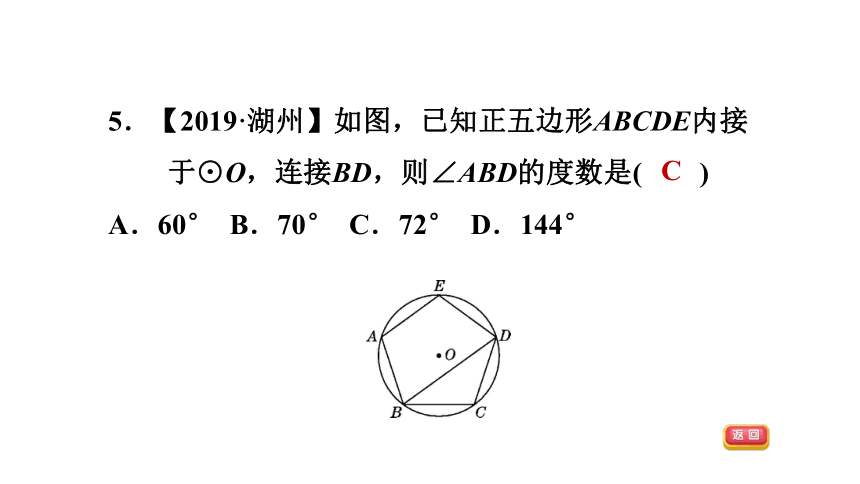
5.【2019·湖州】如图,已知正五边形ABCDE内接于⊙O,连接BD,则∠ABD的度数是( )
A.60° B.70° C.72° D.144°
A
7.【2018·威海】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,则图中阴影部分的面积是( )
A.18+36π
B.24+18π
C.18+18π
D.12+18π
【答案】C
8.【2018·宜宾】刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设⊙O的半径为1,若用⊙O的外切正六边形的面积S来近似估计⊙O的面积,则S=________.(结果保留根号)
9.如图,按要求画出⊙O的内接正多边形.
(1)正三角形;(2)正方形;(3)正六边形;(4)正八边形.
解:如图所示.
【答案】 A
11.【2019·镇江】在三角形纸片ABC(如图①)中,∠BAC=78°,AC=10,小霞用5张这样的三角形纸片拼成了一个内外都是正五边形的图形(如图②).
(1)∠ABC=________°;
30°
(2)求正五边形GHMNC的边GC的长.
(参考值:sin 78°≈0.98,cos 78°≈0.21,tan 78°≈4.70)
12.作图与证明:
如图,已知⊙O和⊙O上的一点A,请完成下列任务:
(1)作⊙O的内接正六边形ABCDEF;
解:如图,先作直径AD,然后分别以A,D为圆心,OA长为半径画弧,分别交⊙O于点B,F,C,E,连接AB,BC,CD,DE,EF,AF,则正六边形ABCDEF即为所求.(作法不唯一)
(2)连接BF,CE,判断四边形BCEF的形状并加以证明.
14.如图①②③④,正三角形ABC、正四边形ABCD、正五边形ABCDE、正n边形ABCD…分别内接于⊙O,点M,N分别从点B,C同时开始以相同的速度在⊙O上逆时针运动,AM与BN相交于点P.
(1)图①中,∠APN=________.
(2)图②中,∠APN=________,
图③中,∠APN=________.
60°
90°
108°
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案).
人教版九年级上
8 圆内接正多边形
第三章 圆
答案显示
B
B
C
C
A
D
C
答案显示
图略.
见习题.
A
(1)30°;(2)9.6.
1.正多边形的中心角与该正多边形的一个内角的关系为( )
A.两角互余 B.两角互补
C.两角互余或互补 D.不能确定
B
【答案】C
B
D
C
5.【2019·湖州】如图,已知正五边形ABCDE内接于⊙O,连接BD,则∠ABD的度数是( )
A.60° B.70° C.72° D.144°
A
7.【2018·威海】如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,则图中阴影部分的面积是( )
A.18+36π
B.24+18π
C.18+18π
D.12+18π
【答案】C
8.【2018·宜宾】刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积,设⊙O的半径为1,若用⊙O的外切正六边形的面积S来近似估计⊙O的面积,则S=________.(结果保留根号)
9.如图,按要求画出⊙O的内接正多边形.
(1)正三角形;(2)正方形;(3)正六边形;(4)正八边形.
解:如图所示.
【答案】 A
11.【2019·镇江】在三角形纸片ABC(如图①)中,∠BAC=78°,AC=10,小霞用5张这样的三角形纸片拼成了一个内外都是正五边形的图形(如图②).
(1)∠ABC=________°;
30°
(2)求正五边形GHMNC的边GC的长.
(参考值:sin 78°≈0.98,cos 78°≈0.21,tan 78°≈4.70)
12.作图与证明:
如图,已知⊙O和⊙O上的一点A,请完成下列任务:
(1)作⊙O的内接正六边形ABCDEF;
解:如图,先作直径AD,然后分别以A,D为圆心,OA长为半径画弧,分别交⊙O于点B,F,C,E,连接AB,BC,CD,DE,EF,AF,则正六边形ABCDEF即为所求.(作法不唯一)
(2)连接BF,CE,判断四边形BCEF的形状并加以证明.
14.如图①②③④,正三角形ABC、正四边形ABCD、正五边形ABCDE、正n边形ABCD…分别内接于⊙O,点M,N分别从点B,C同时开始以相同的速度在⊙O上逆时针运动,AM与BN相交于点P.
(1)图①中,∠APN=________.
(2)图②中,∠APN=________,
图③中,∠APN=________.
60°
90°
108°
(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案).
