苏教版高中必修2.2.2减函数 课件(共21张)
文档属性
| 名称 | 苏教版高中必修2.2.2减函数 课件(共21张) |
|
|
| 格式 | zip | ||
| 文件大小 | 12.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 21:38:48 | ||
图片预览



文档简介
(共21张PPT)
2.2.1 减函数
普通高中课程标准实验教科书 《数学》 必修一第二章 苏教版
2020年01月01日
START
<<<
汇报人:熊猫办公 时间:XX年XX月
1.1 山峰变化趋势
问题探究
概念新知
典型例题
课堂小结
情景导入
情景导入
1.1 山峰变化趋势
2.1 减函数的定义
请学生们尝试根据增函数的定义推导出减函数的定义!
问题探究
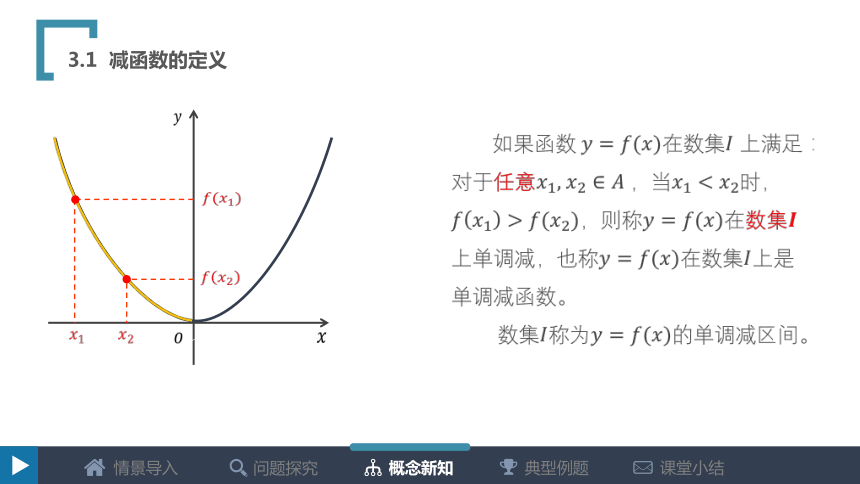
如果函数在数集 上满足:
对于任意 ,当 时,
,则称在数集
上单调减,也称在数集上是
单调减函数。
数集称为的单调减区间。
3.1 减函数的定义
概念新知
典型例题
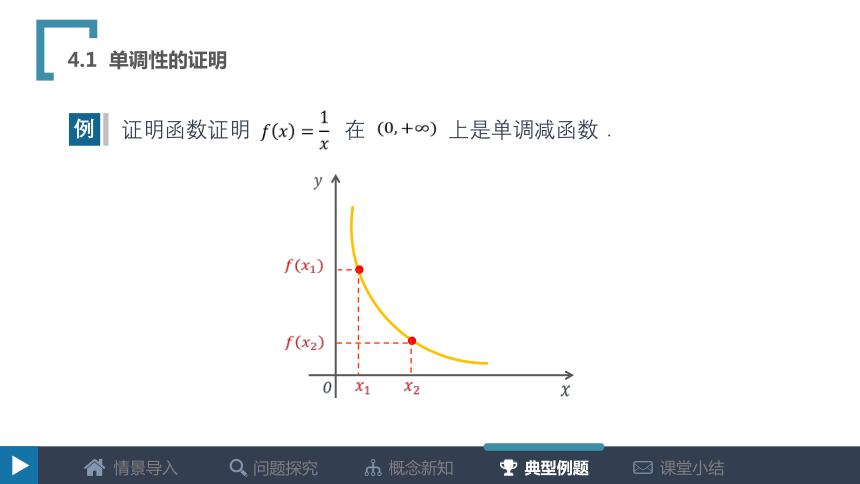
4.1 单调性的证明
证明函数证明 在 上是单调减函数.
例
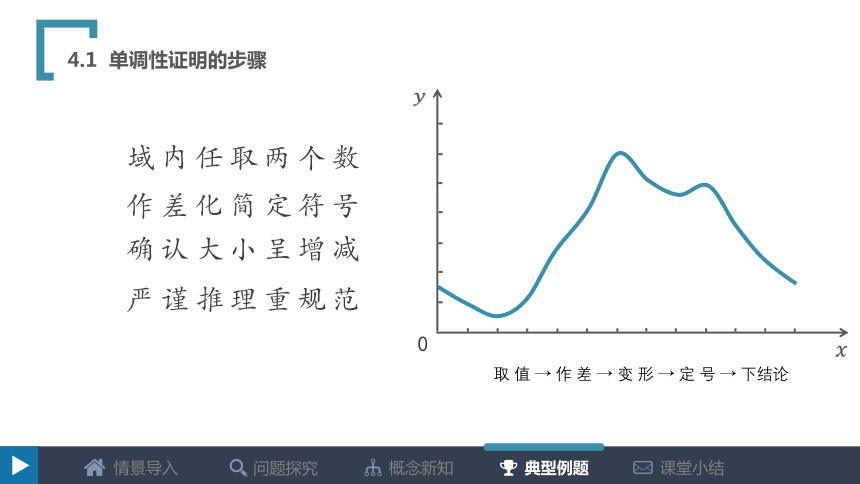
4.1 单调性证明的步骤
域内任取两个数
作差化简定符号
确认大小呈增减
严谨推理重规范
0
取?值?→?作?差?→?变?形?→?定?号?→?下结论
4.2 图像特征
观察下面函数图像,说出函数的单调区间
例
4.2 图像特征
观察下面函数图像,说出函数的单调区间
例
4.2 图像特征
观察下面函数图像,说出函数的单调区间
例
4.2 图像特征
观察下面函数图像,说出函数的单调区间
例
4.2 单调区间
4.3 单调性性质的应用
(1)定义在上的单调函数满足,那么函数是上的单调增函数还是单调减函数?请说明理由。
例
(2)若定义在上的单调减函数满足 ,求实数的取值范围。
4.3 单调性性质的应用
若定义在上的单调减函数满足 ,如何求实数的取值范围?
变
5.1 课堂小结
1. 单调函数的概念
2. 单调函数图像特征
3. 单调区间
4. 单调性证明的一般步骤
5. 性质的应用
华尔街股票行情走势图
0
0
℃
2
4
6
8
10
12
14
16
18
20
22
24
4
8
12
16
20
24
26
某地24小时气温变化图
艾宾浩斯记忆曲线
0
THANKS
N
2.2.1 减函数
普通高中课程标准实验教科书 《数学》 必修一第二章 苏教版
2020年01月01日
START
<<<
汇报人:熊猫办公 时间:XX年XX月
1.1 山峰变化趋势
问题探究
概念新知
典型例题
课堂小结
情景导入
情景导入
1.1 山峰变化趋势
2.1 减函数的定义
请学生们尝试根据增函数的定义推导出减函数的定义!
问题探究
如果函数在数集 上满足:
对于任意 ,当 时,
,则称在数集
上单调减,也称在数集上是
单调减函数。
数集称为的单调减区间。
3.1 减函数的定义
概念新知
典型例题
4.1 单调性的证明
证明函数证明 在 上是单调减函数.
例
4.1 单调性证明的步骤
域内任取两个数
作差化简定符号
确认大小呈增减
严谨推理重规范
0
取?值?→?作?差?→?变?形?→?定?号?→?下结论
4.2 图像特征
观察下面函数图像,说出函数的单调区间
例
4.2 图像特征
观察下面函数图像,说出函数的单调区间
例
4.2 图像特征
观察下面函数图像,说出函数的单调区间
例
4.2 图像特征
观察下面函数图像,说出函数的单调区间
例
4.2 单调区间
4.3 单调性性质的应用
(1)定义在上的单调函数满足,那么函数是上的单调增函数还是单调减函数?请说明理由。
例
(2)若定义在上的单调减函数满足 ,求实数的取值范围。
4.3 单调性性质的应用
若定义在上的单调减函数满足 ,如何求实数的取值范围?
变
5.1 课堂小结
1. 单调函数的概念
2. 单调函数图像特征
3. 单调区间
4. 单调性证明的一般步骤
5. 性质的应用
华尔街股票行情走势图
0
0
℃
2
4
6
8
10
12
14
16
18
20
22
24
4
8
12
16
20
24
26
某地24小时气温变化图
艾宾浩斯记忆曲线
0
THANKS
N
