北师大版高中数学必修4第一章《单位圆与任意角的正、余弦函数定义,周期性》课件(共16张PPT)
文档属性
| 名称 | 北师大版高中数学必修4第一章《单位圆与任意角的正、余弦函数定义,周期性》课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 527.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-28 01:10:59 | ||
图片预览





文档简介
(共16张PPT)
§4.1 单位圆与任意角的正弦函数、余弦函数的定义
§4.2 单位圆与周期性
江西省2020年寒假及春季学期延期开学期间线上教育课程
北师大版 高中数学 必修4
第一章 三角函数
一、创设情境,导入新课
在直角三角形中,锐角 的正弦函数、余弦函数定义:
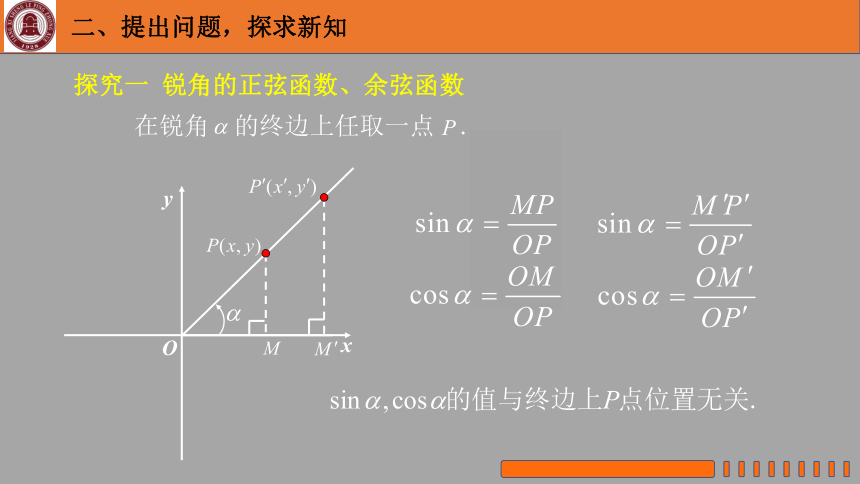
探究一 锐角的正弦函数、余弦函数
y
x
O
二、提出问题,探求新知
在锐角 的终边上任取一点 .
探究一 锐角的正弦函数、余弦函数
在锐角 的终边上取一点 ,使得 ,此时 点为锐角 终边与单位圆的交点,记作 .
在锐角 的终边上取一点
二、提出问题,探求新知
y
x
O
任意锐角
唯一确定的
(实数)
任意锐角
唯一确定的
(实数)
是 的正弦函数,记作
是 的余弦函数,记作
二、提出问题,探求新知
y
x
O
探究一 锐角的正弦函数、余弦函数
在锐角 的终边上取一点 ,使得 ,此时 点为锐角 终边与单位圆的交点,记作 .
对于任意角 ,使角 的顶点与原点重合,始边与 轴的非负半轴重合,终边与单位圆交于唯一的点 ,我们把点 的纵坐标 定义为角 的正弦函数,
记作 ;
点 的横坐标 定义为角 的余弦函数,记作 .
二、提出问题,探求新知
注意:正弦函数、余弦函数都是以角为自变量的函数.
y
x
O
正弦函数 ;余弦函数 .
思考:已知函数 ,
解
+
探究二 任意角的正弦函数、余弦函数
第一
象限 第二
象限 第三
象限 第四
象限
三、分析思考,加深理解
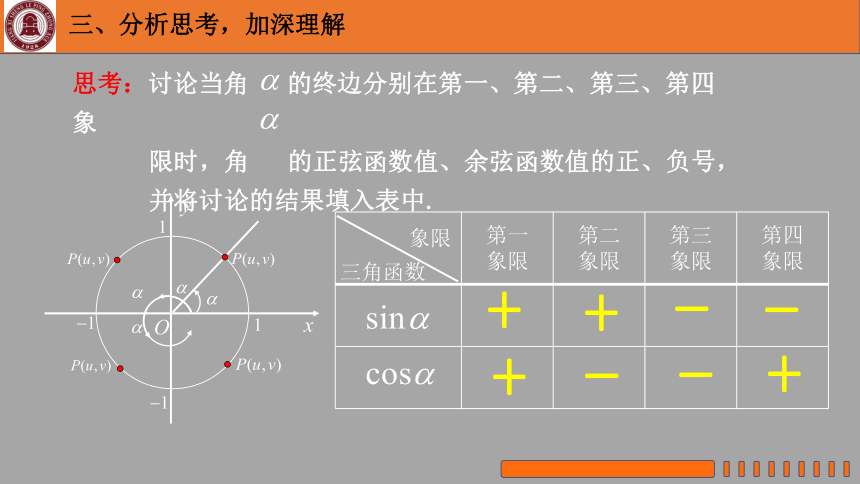
思考:讨论当角 的终边分别在第一、第二、第三、第四象
限时,角 的正弦函数值、余弦函数值的正、负号,
并将讨论的结果填入表中.
y
x
O
象限
三角函数
+
+
+
+
-
-
-
-
P
N
M
例1 假设角 的顶点是直角坐标系的原点,始边与 轴的非负半轴重合,已知角 终边上任一点 ,求角 的正弦函数值、余弦函数值.
解
四、强化训练,巩固双基
先考虑角 终边不在坐标轴上的情形,如图.
当角 终边在坐标轴上时,容易验证上述计算公式仍成立.
y
x
O
四、强化训练,巩固双基
点评:若已知角 的大小,可求出角 终边与单位圆的交点,然后再利用定义求正、余弦函数值.
例2 求 的正弦函数值、余弦函数值.
解
y
x
O
画出 的终边,并求其与单位圆的交点坐标
例3 确定下列三角函数值的符号:
(1)因为260o是第三象限角,所以cos260o<0;
(2)因为 是第四象限角,所以 .
四、强化训练,巩固双基
解
动手实践 在直角坐标系的单位圆中,画出下列各特殊角,求各个角终边与单位圆的交点坐标,并将各特殊角的正弦函数值、余弦函数值填入下表
观察表格中数据,你能发现函数 和 的变化有什么特点吗?
三、分析思考,加深理解
同理,终边相同角的余弦函数值相等,即
观察右图,设任意角 与单位圆的交点为 ,则与角 终边相同的角为 ,角 的终边与单位圆也交于点 ,所以 与 取正弦对应同一个实数 ,即终边相同的角的正弦函数值相等,有
即 ;
探究三 周期函数
三、分析思考,加深理解
一般地,对于函数 ,如果存在非零实数 ,对定义域内的任意一个 值,都有 .
我们就把 称为周期函数, 称为这个函数的周期.
把这种随自变量的变化呈周期性变化的函数叫作周期函数.正弦函数、余弦函数是周期函数,称 为正弦函数、余弦函数的周期.
探究三 周期函数
三、分析思考,加深理解
例如, , , , 等都是他们的周期.其中 是正弦函数、余弦函数正周期中最小的一个,称为最小正周期,简称为周期.
因为 ,所以 是 的周期,对吗?
例4 求下列三角函数值:
四、强化训练,巩固双基
解
五、课堂小结,升华提高
知识与技能:
(1)任意角三角函数的定义(单位圆);
(2) 定义判定正弦函数值、余弦函数值的符号;
(3) 周期函数.
思想与方法:
单位圆、坐标法、特殊到一般、数形结合、转化、分类讨论,
函数思想.
六、作业布置
1.习题2,4
2.A组第2,3,4题
同学们再见!
§4.1 单位圆与任意角的正弦函数、余弦函数的定义
§4.2 单位圆与周期性
江西省2020年寒假及春季学期延期开学期间线上教育课程
北师大版 高中数学 必修4
第一章 三角函数
一、创设情境,导入新课
在直角三角形中,锐角 的正弦函数、余弦函数定义:
探究一 锐角的正弦函数、余弦函数
y
x
O
二、提出问题,探求新知
在锐角 的终边上任取一点 .
探究一 锐角的正弦函数、余弦函数
在锐角 的终边上取一点 ,使得 ,此时 点为锐角 终边与单位圆的交点,记作 .
在锐角 的终边上取一点
二、提出问题,探求新知
y
x
O
任意锐角
唯一确定的
(实数)
任意锐角
唯一确定的
(实数)
是 的正弦函数,记作
是 的余弦函数,记作
二、提出问题,探求新知
y
x
O
探究一 锐角的正弦函数、余弦函数
在锐角 的终边上取一点 ,使得 ,此时 点为锐角 终边与单位圆的交点,记作 .
对于任意角 ,使角 的顶点与原点重合,始边与 轴的非负半轴重合,终边与单位圆交于唯一的点 ,我们把点 的纵坐标 定义为角 的正弦函数,
记作 ;
点 的横坐标 定义为角 的余弦函数,记作 .
二、提出问题,探求新知
注意:正弦函数、余弦函数都是以角为自变量的函数.
y
x
O
正弦函数 ;余弦函数 .
思考:已知函数 ,
解
+
探究二 任意角的正弦函数、余弦函数
第一
象限 第二
象限 第三
象限 第四
象限
三、分析思考,加深理解
思考:讨论当角 的终边分别在第一、第二、第三、第四象
限时,角 的正弦函数值、余弦函数值的正、负号,
并将讨论的结果填入表中.
y
x
O
象限
三角函数
+
+
+
+
-
-
-
-
P
N
M
例1 假设角 的顶点是直角坐标系的原点,始边与 轴的非负半轴重合,已知角 终边上任一点 ,求角 的正弦函数值、余弦函数值.
解
四、强化训练,巩固双基
先考虑角 终边不在坐标轴上的情形,如图.
当角 终边在坐标轴上时,容易验证上述计算公式仍成立.
y
x
O
四、强化训练,巩固双基
点评:若已知角 的大小,可求出角 终边与单位圆的交点,然后再利用定义求正、余弦函数值.
例2 求 的正弦函数值、余弦函数值.
解
y
x
O
画出 的终边,并求其与单位圆的交点坐标
例3 确定下列三角函数值的符号:
(1)因为260o是第三象限角,所以cos260o<0;
(2)因为 是第四象限角,所以 .
四、强化训练,巩固双基
解
动手实践 在直角坐标系的单位圆中,画出下列各特殊角,求各个角终边与单位圆的交点坐标,并将各特殊角的正弦函数值、余弦函数值填入下表
观察表格中数据,你能发现函数 和 的变化有什么特点吗?
三、分析思考,加深理解
同理,终边相同角的余弦函数值相等,即
观察右图,设任意角 与单位圆的交点为 ,则与角 终边相同的角为 ,角 的终边与单位圆也交于点 ,所以 与 取正弦对应同一个实数 ,即终边相同的角的正弦函数值相等,有
即 ;
探究三 周期函数
三、分析思考,加深理解
一般地,对于函数 ,如果存在非零实数 ,对定义域内的任意一个 值,都有 .
我们就把 称为周期函数, 称为这个函数的周期.
把这种随自变量的变化呈周期性变化的函数叫作周期函数.正弦函数、余弦函数是周期函数,称 为正弦函数、余弦函数的周期.
探究三 周期函数
三、分析思考,加深理解
例如, , , , 等都是他们的周期.其中 是正弦函数、余弦函数正周期中最小的一个,称为最小正周期,简称为周期.
因为 ,所以 是 的周期,对吗?
例4 求下列三角函数值:
四、强化训练,巩固双基
解
五、课堂小结,升华提高
知识与技能:
(1)任意角三角函数的定义(单位圆);
(2) 定义判定正弦函数值、余弦函数值的符号;
(3) 周期函数.
思想与方法:
单位圆、坐标法、特殊到一般、数形结合、转化、分类讨论,
函数思想.
六、作业布置
1.习题2,4
2.A组第2,3,4题
同学们再见!
