北师大版高中数学选修2-1第一章《常用逻辑用语复习小结》课件(共21张PPT)
文档属性
| 名称 | 北师大版高中数学选修2-1第一章《常用逻辑用语复习小结》课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-28 01:16:48 | ||
图片预览





文档简介
(共19张PPT)
常用逻辑用语复习小结
北师大版-高中数学选修2-1第一章:常用逻辑用语
赣
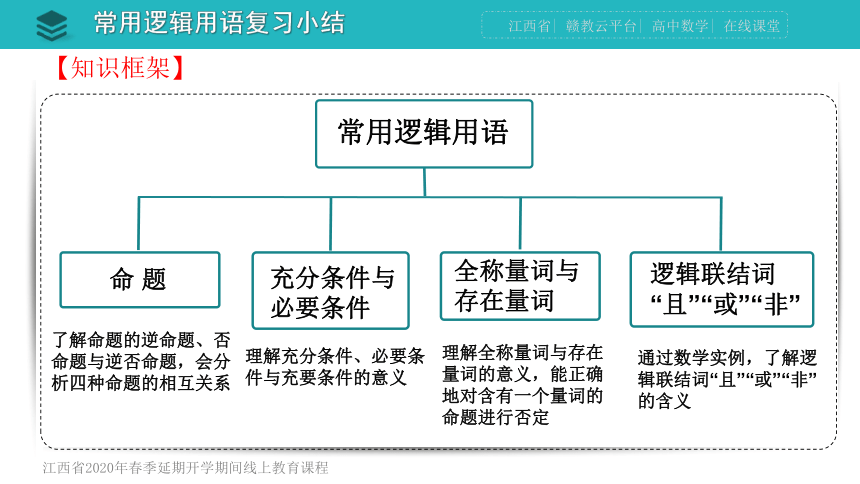
常用逻辑用语
命 题
充分条件与必要条件
全称量词与存在量词
逻辑联结词“且”“或”“非”
【知识框架】
了解命题的逆命题、否命题与逆否命题,会分析四种命题的相互关系
理解充分条件、必要条件与充要条件的意义
理解全称量词与存在量词的意义,能正确地对含有一个量词的命题进行否定
通过数学实例,了解逻辑联结词“且”“或”“非”的含义
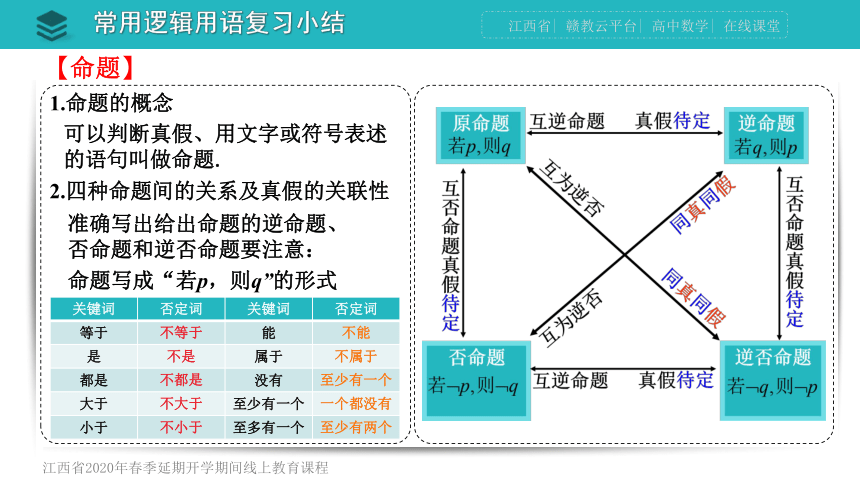
1.命题的概念
可以判断真假、用文字或符号表述的语句叫做命题.
【命题】
2.四种命题间的关系及真假的关联性
命题写成“若p,则q”的形式
准确写出给出命题的逆命题、
否命题和逆否命题要注意:
关键词 否定词 关键词 否定词
等于 不等于 能 不能
是 不是 属于 不属于
都是 不都是 没有 至少有一个
大于 不大于 至少有一个 一个都没有
小于 不小于 至多有一个 至少有两个
等价转化的思想——借助命题的等价形式(逆否命题)的真假帮助判定.
【命题】
互为逆否关系的命题真假性相同.
真
真
假
假
原命题是真命题,逆命题是假命题.
1.从概念角度理解:
设命题为“若p,则q”,
【充分条件与必要条件】
2.从集合角度理解:
若 A={x|p(x)成立},B={x|q(x)成立}
【充分条件与必要条件】
等价转化的思想——充分条件与必要条件的判定可以利用互为逆否关系的命题形式进行转化
【充分条件与必要条件】
等价转化的思想——充分条件与必要条件的判定可以利用题设的充要条件进行转化
【充分条件与必要条件】
充分条件
充要条件
必要条件
引入新的数学对象后,需要研究如何判断一个对象是否是我们引入的新对象,就是要探究判定定理.
引入新的数学对象后,需要研究这个对象具有什么性质,通常我们以性质定理的形式给出判定一个事物的必要条件.
一个事物的充要条件可以帮助我们从不同的角度,全面的反映同一个事物的面貌.
充要条件
解三角形
数列
平面向量
充分条件
必要条件
【全称量词与存在量词】
同一个全称命题或特称命题,由于自然语言的不同,可以有不同的表述方法,在应用中可以灵活选择.
全称命题的否定是特称命题,特称命题的否定是全称命题.
全称量词与存在量词
每一个等腰三角形的两个底角相等
过直线外一点存在唯一的一条直线与该直线平行
【全称量词与存在量词】
【全称量词与存在量词】
等价转化——借助全称量词与存在量词对条件进行转化
【逻辑联结词“且”“或”“非”】
否定命题时,要注意特殊的词,如“全”“都”等.常见关键词及其否定形式如下表. ?
都是
不都是
至少有一个不是
【逻辑联结词“且”“或”“非”】
关键词 否定词 关键词 否定词
等于 不等于 能 不能
是 不是 属于 不属于
都是 不都是 没有 至少有一个
大于 不大于 至少有一个 一个都没有
小于 不小于 至多有一个 至少有两个
【课堂小结】
等价转化的思想
正确地使用常用逻辑用语,不仅是学习这一部分的内容,而且还需要在今后的学习中,通过不断地正确使用常用逻辑用语,加深对常用逻辑用语的认识.
【课后作业】
3.请同学们用充分条件、必要条件、充要条件、全称量词、存在量词梳理知识(各举出2-3个例子)
充分条件 必要条件 充要条件 全称命题与特称命题
必修1
必修2
必修3
必修4
必修5
【参考答案】
谢谢
THANKS
常用逻辑用语复习小结
北师大版-高中数学选修2-1第一章:常用逻辑用语
赣
常用逻辑用语
命 题
充分条件与必要条件
全称量词与存在量词
逻辑联结词“且”“或”“非”
【知识框架】
了解命题的逆命题、否命题与逆否命题,会分析四种命题的相互关系
理解充分条件、必要条件与充要条件的意义
理解全称量词与存在量词的意义,能正确地对含有一个量词的命题进行否定
通过数学实例,了解逻辑联结词“且”“或”“非”的含义
1.命题的概念
可以判断真假、用文字或符号表述的语句叫做命题.
【命题】
2.四种命题间的关系及真假的关联性
命题写成“若p,则q”的形式
准确写出给出命题的逆命题、
否命题和逆否命题要注意:
关键词 否定词 关键词 否定词
等于 不等于 能 不能
是 不是 属于 不属于
都是 不都是 没有 至少有一个
大于 不大于 至少有一个 一个都没有
小于 不小于 至多有一个 至少有两个
等价转化的思想——借助命题的等价形式(逆否命题)的真假帮助判定.
【命题】
互为逆否关系的命题真假性相同.
真
真
假
假
原命题是真命题,逆命题是假命题.
1.从概念角度理解:
设命题为“若p,则q”,
【充分条件与必要条件】
2.从集合角度理解:
若 A={x|p(x)成立},B={x|q(x)成立}
【充分条件与必要条件】
等价转化的思想——充分条件与必要条件的判定可以利用互为逆否关系的命题形式进行转化
【充分条件与必要条件】
等价转化的思想——充分条件与必要条件的判定可以利用题设的充要条件进行转化
【充分条件与必要条件】
充分条件
充要条件
必要条件
引入新的数学对象后,需要研究如何判断一个对象是否是我们引入的新对象,就是要探究判定定理.
引入新的数学对象后,需要研究这个对象具有什么性质,通常我们以性质定理的形式给出判定一个事物的必要条件.
一个事物的充要条件可以帮助我们从不同的角度,全面的反映同一个事物的面貌.
充要条件
解三角形
数列
平面向量
充分条件
必要条件
【全称量词与存在量词】
同一个全称命题或特称命题,由于自然语言的不同,可以有不同的表述方法,在应用中可以灵活选择.
全称命题的否定是特称命题,特称命题的否定是全称命题.
全称量词与存在量词
每一个等腰三角形的两个底角相等
过直线外一点存在唯一的一条直线与该直线平行
【全称量词与存在量词】
【全称量词与存在量词】
等价转化——借助全称量词与存在量词对条件进行转化
【逻辑联结词“且”“或”“非”】
否定命题时,要注意特殊的词,如“全”“都”等.常见关键词及其否定形式如下表. ?
都是
不都是
至少有一个不是
【逻辑联结词“且”“或”“非”】
关键词 否定词 关键词 否定词
等于 不等于 能 不能
是 不是 属于 不属于
都是 不都是 没有 至少有一个
大于 不大于 至少有一个 一个都没有
小于 不小于 至多有一个 至少有两个
【课堂小结】
等价转化的思想
正确地使用常用逻辑用语,不仅是学习这一部分的内容,而且还需要在今后的学习中,通过不断地正确使用常用逻辑用语,加深对常用逻辑用语的认识.
【课后作业】
3.请同学们用充分条件、必要条件、充要条件、全称量词、存在量词梳理知识(各举出2-3个例子)
充分条件 必要条件 充要条件 全称命题与特称命题
必修1
必修2
必修3
必修4
必修5
【参考答案】
谢谢
THANKS
