华东师大版数学八年级下册第19章《矩形、菱形与正方形》单元测试卷(含详细答案)
文档属性
| 名称 | 华东师大版数学八年级下册第19章《矩形、菱形与正方形》单元测试卷(含详细答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 144.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 00:00:00 | ||
图片预览



文档简介
华东师大版八年级下册第19章单元测试卷
满分120分
班级:________姓名:________座位:________成绩:________
一.选择题(共10小题,满分30分)
1.检查一个门框(已知两组对边分别相等)是不是矩形,不可用的方法是( )
A.测量两条对角线是否相等
B.用重锤线检查竖门框是否与地面垂直
C.测量两条对角线是否互相平分
D.测量门框的三个角是否都是直角
2.如图,在菱形ABCD中,对角线AC,BD相交于点O.若∠BAD=50°,则∠CBD=( )
A.25° B.40° C.65° D.75°
3.如图,要使?ABCD成为菱形,则需添加的一个条件是( )
A.AC=AD B.BA=BC C.∠ABC=90° D.AC=BD
4.在矩形ABCD中,对角线AC=10cm,AB:BC=4:3,则它的周长为( )cm.
A.14 B.20 C.28 D.30
5.如图,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是( )
A.6 B.12 C.24 D.48
6.如图,在矩形ABCD中,AB=4,BC=6,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是( )
A.1 B. C.2 D.
7.如图,在一张长方形纸片上画一条线段AB,将右侧部分纸片四边形ABCD沿线段AB翻折至四边形ABC'D',若∠ABC=58°,则∠1=( )
A.60° B.64° C.42° D.52°
8.如图,点E为正方形ABCD内一点,AD=ED,∠AED=70°,连结EC,那么∠AEC的度数是( )
A.105° B.130° C.135° D.140°
9.如图,四边形ABCD是菱形,DH⊥AB于H,若AC=8,BD=6,则DH的长度为( )
A.2.4 B.3.6 C.4.8 D.7.2
10.如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG;④2HG=AD.正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,满分18分)
11.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,若矩形ABCD的面积是12,那么阴影部分的面积是 .
12.如图,四边形ABCD中,对角线AC,BD相等且互相平分,再添加一个条件,使得四边形ABCD是正方形,可添加的条件是 .(写出一个条件即可)
13.如图,矩形ABCD中,直线MN垂直平分AC,与CD,AB分别交于点M,N.若DM=2,CM=3,则矩形的对角线AC的长为 .
14.如图,已知菱形ABCD的边长为2,∠CDA=120°,则对角线AC的长为 .
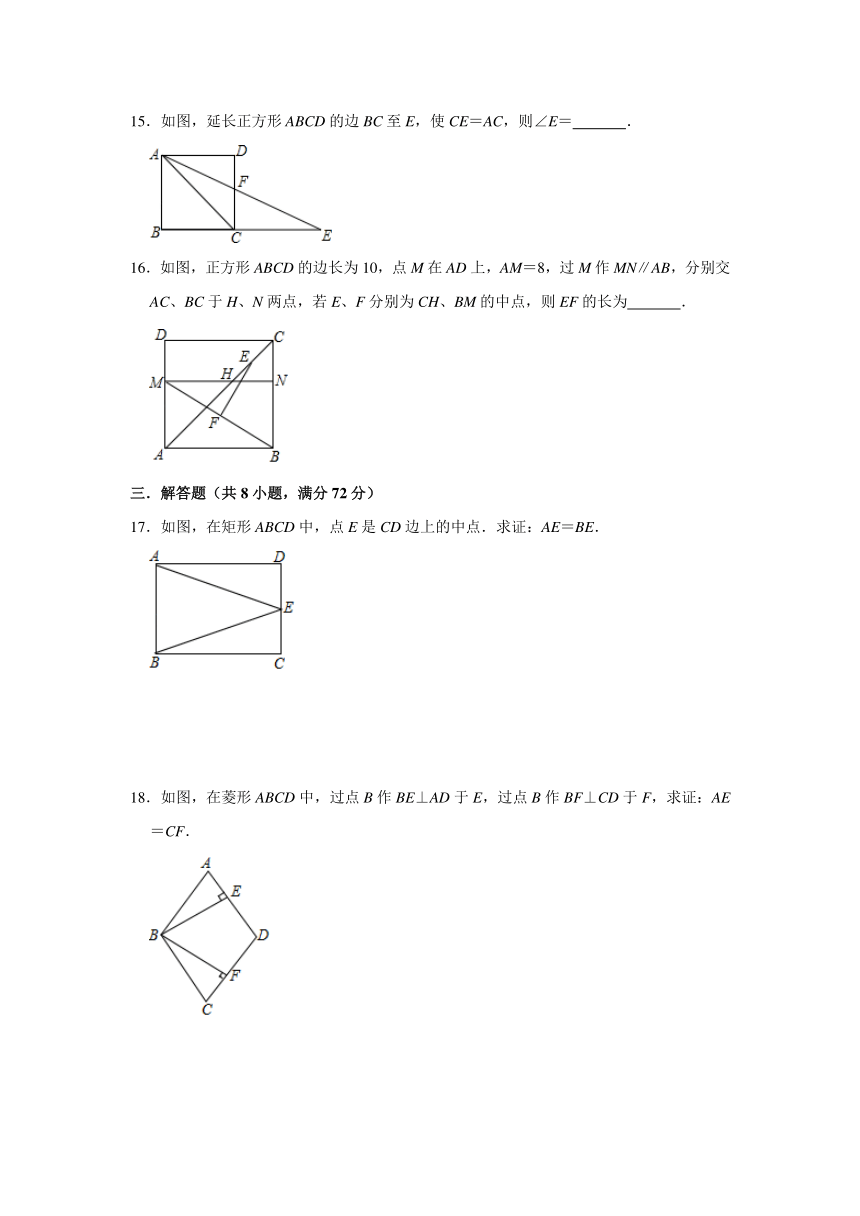
15.如图,延长正方形ABCD的边BC至E,使CE=AC,则∠E= .
16.如图,正方形ABCD的边长为10,点M在AD上,AM=8,过M作MN∥AB,分别交AC、BC于H、N两点,若E、F分别为CH、BM的中点,则EF的长为 .
三.解答题(共8小题,满分72分)
17.如图,在矩形ABCD中,点E是CD边上的中点.求证:AE=BE.
18.如图,在菱形ABCD中,过点B作BE⊥AD于E,过点B作BF⊥CD于F,求证:AE=CF.
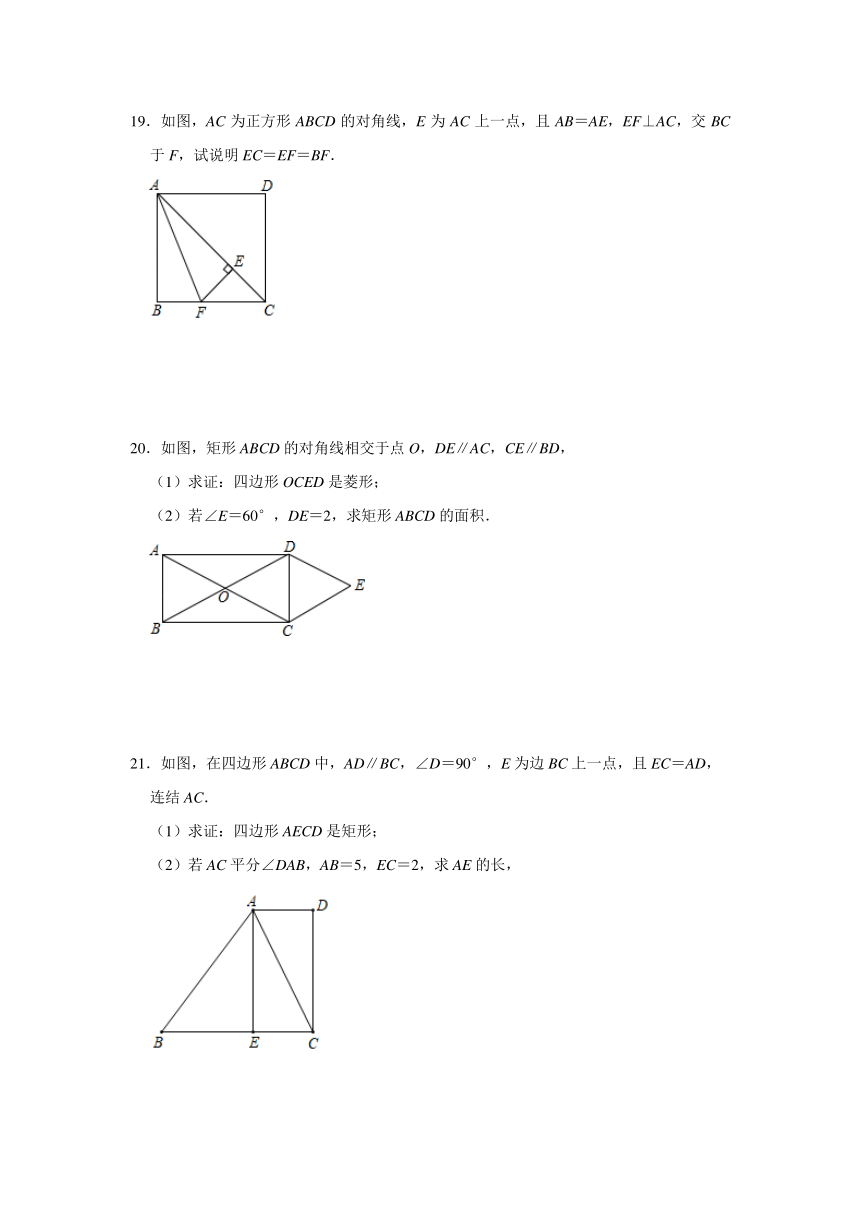
19.如图,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC,交BC于F,试说明EC=EF=BF.
20.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD,
(1)求证:四边形OCED是菱形;
(2)若∠E=60°,DE=2,求矩形ABCD的面积.
21.如图,在四边形ABCD中,AD∥BC,∠D=90°,E为边BC上一点,且EC=AD,
连结AC.
(1)求证:四边形AECD是矩形;
(2)若AC平分∠DAB,AB=5,EC=2,求AE的长,
22.如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM与BD相交于点F.
(1)求证:OE=OF;
(2)如图2若点E在AC的延长线上,AM⊥BE于点M,AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
23.在Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AC=BD,AC、BD相交于点G,过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE、BF相交于点H.
(1)证明:△ABD≌△BAC.
(2)证明:四边形AHBG是菱形.
(3)若AB=BC,证明四边形AHBG是正方形.
24.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
参考答案
一.选择题(共10小题)
1.【解答】解:∵门框两组对边分别相等,
∴门框是个平行四边形,
∵对角线相等的平行四边形是矩形,
故A不符合题意;
∵竖门框与地面垂直,门框一定是矩形;
故B不符合题意,
∵对角线互相平分的四边形是平行四边形,
∴C符合题意,
∵三个角都是直角的四边形是矩形,
故D不符合题意;
故选:C.
2.【解答】解:∵四边形ABCD为菱形,
∴∠DAB+∠ABC=180°,BD平分∠ABC,
∵∠BAD=50°,
∴∠ABC=130°,
∴∠CBD=∠ABC=65°,
故选:C.
3.【解答】解:邻边相等的平行四边形为菱形.如图,要使?ABCD成为菱形,则需添加的一个条件是BA=BC.
故选:B.
4.【解答】解:设AB=4xcm,则BC=3xcm,
∵四边形ABCD是矩形,
∴∠B=90°,AB=CD,AD=BC,
∴AC===5x(cm),
∴5x=10cm,
∴x=2cm,
∴AB=8cm,BC=6cm,
∴矩形ABCD的周长=2(8+6)=28(cm),
故选:C.
5.【解答】解:∵菱形ABCD的周长是20,
∴AB=20÷4=5,AC⊥BD,OB=BD=3,
∴OA==4,
∴AC=2OA=8,
∴菱形ABCD的面积是:AC?BD=×8×6=24.
故选:C.
6.【解答】解:连接CE,如图所示:
∵四边形ABCD是矩形,
∴∠ADC=90°,CD=AB=4,AD=BC=6,OA=OC,
∵EF⊥AC,
∴AE=CE,
设DE=x,则CE=AE=6﹣x,
在Rt△CDE中,由勾股定理得:x2+42=(6﹣x)2,
解得:x=,
即DE=;
故选:D.
7.【解答】解:∵AD∥BC,
∴∠ABC+∠BAD=180°,且∠ABC=58°,
∴∠BAD=122°,
∵将右侧部分纸片四边形ABCD沿线段AB翻折至四边形ABC'D',
∴∠BAD=∠BAD'=122°,
∴∠1=122°+122°﹣180°=64°,
故选:B.
8.【解答】解:∵AD=DE,
∴∠DAE=∠AED=70°,
∴∠ADE=180°﹣70°﹣70°=40°,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠EDC=50°,
∴DC=DE,
∴∠DEC=∠DCE=(180°﹣50°)=65°,
∴∠AEC=∠AED+∠DEC=135°,
故选:C.
9.【解答】解:设AC与BD的交点为O,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=4,OB=OD=3,
∴AB=5,
∴S菱形ABCD=AC?BD=AB?DH,
∴DH==4.8.
故选:C.
10.【解答】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=90°,
∵点E、F、H分别是AB、BC、CD的中点,
∴BE=CF,
在△BCE与△CDF中,,
∴△BCE≌△CDF,(SAS),
∴∠ECB=∠CDF,
∵∠BCE+∠ECD=90°,
∴∠ECD+∠CDF=90°,
∴∠CGD=90°,
∴CE⊥DF;故①正确;
在Rt△CGD中,H是CD边的中点,
∴HG=CD=AD,
即2HG=AD;故④正确;
连接AH,如图所示:
同理可得:AH⊥DF,
∵HG=HD=CD,
∴DK=GK,
∴AH垂直平分DG,
∴AG=AD;
若AG=DG,则△ADG是等边三角形,
则∠ADG=60°,∠CDF=30°,
而CF=CD≠DF,
∴∠CDF≠30°,
∴∠ADG≠60°,
∴AG≠DG,故②错误;
∴∠DAG=2∠DAH,
同理:△ADH≌△DCF,
∴∠DAH=∠CDF,
∵GH=DH,
∴∠HDG=∠HGD,
∴∠GHC=∠HDG+∠HGD=2∠CDF,
∴∠CHG=∠DAG;故③正确;
正确的结论有3个,
故选:C.
二.填空题(共6小题)
11.【解答】解:∵四边形ABCD是矩形,
∴AB∥CD,OA=OC,
∴∠EAO=∠FCO,
在△AOE和△COF中,,
∴△AOE≌△COF(ASA),
∴S△AOE=S△COF,
∴S阴=S△COD=S矩形ABCD=3,
故答案为:3.
12.【解答】解:∵对角线AC与BD互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD为矩形,
需添加一个条件是:AB=BC,
∴四边形ABCD是正方形;答案不唯一,
故答案为:AB=BC.
13.【解答】解:如图,连接AM.
∵直线MN垂直平分AC,
∴MA=MC=3,
∵四边形ABCD是矩形,
∴∠D=90°,
∵DM=2,MA=3,
∴AD2=AM2﹣DM2=32﹣22=5,
∴AC===;
故答案为:.
14.【解答】解:连接BD交AC于O,如图,
∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC,AD=AB=2,
∴∠CDA=120°,
∴∠DAB=60°,
∴△ADB为等边三角形,
∴OA=AB=,
∴AC=2OA=2.
故答案为:2.
15.【解答】解:∵四边形ABCD是正方形,
∴∠ACB=45°,
∵AC=CE,
∴∠E=∠CAF,
∵∠ACB是△ACE的外角,
∴∠E=∠ACB=22.5°,
故答案为:22.5°.
16.【解答】解:过F作FG⊥BC于点G,过E作EP⊥BC于点P,EK⊥FG于点K交MN于点Q,如图所示:
∵四边形ABCD是正方形,
∴AD∥BC,BC=10,
∵MN∥AB,
∴四边形ABNM是矩形,
∴BN=AM=8,MN=10,
∴CN=2,
∵AC是正方形ABCD的对角线,
∴∠CHN=∠HCN=45°,
∴HN=CN=2,
∵E为CH的中点,EP⊥BC,
∴EP是△CHN的中位线,
∴EQ=EP=HN=1,CP=PN=CN=1,
∵F为BM的中点,FG⊥BC,
∴FG是△BMN的中位线,
∴FG=MN=5,BG=NG=BN=4,
∵EK⊥FG,∴四边形PEQN是正方形,四边形QKGN是矩形,
∴GK=EP=1,QK=NG=4,
∴EK=EQ+QK=5,FK=FG﹣GK=4,
在Rt△EFK中,EF===.
三.解答题(共8小题)
17.【解答】证明:∵四边形ABCD是矩形,
∴AD=BC,∠D=∠C=90°,
∵E为CD边上的中点,
∴DE=CE,
∴△ADE≌△BCE(SAS),
∴AE=BE.
18.【解答】证明:∵菱形ABCD,
∴BA=BC,∠A=∠C,
∵BE⊥AD,BF⊥CD,
∴∠BEA=∠BFC=90°,
在△ABE与△CBF中
,
∴△ABE≌△CBF(AAS),
∴AE=CF.
19.【解答】解:在Rt△AEF和Rt△ABF中,
,
∴Rt△AEF≌Rt△ABF(HL),
∴FE=FB.
∵正方形ABCD,
∴∠ACB=∠BCD=45°,
在Rt△CEF中,
∵∠ACB=45°,
∴∠CFE=45°,
∴∠ACB=∠CFE,
∴EC=EF,
∴FB=EC=EF.
20.【解答】证明:(1)∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,
∴OC=OD,
∴四边形OCED是菱形;
(2)∵四边形OCED是菱形
∴OC=OD=DE=2,∠E=∠DOC=60°
∴BD=4,△OCD是等边三角形
∴CD=OC=2
∴BC==2
∴矩形ABCD的面积=BC×CD=4
21.【解答】解:(1)证明:∵AD∥BC,EC=AD,
∴四边形AECD是平行四边形.
又∵∠D=90°,
∴四边形AECD是矩形.
(2)∵AC平分∠DAB.
∴∠BAC=∠DAC.
∵AD∥BC,
∴∠DAC=∠ACB.
∴∠BAC=∠ACB.
∴BA=BC=5.
∵EC=2,
∴BE=3.
∴在Rt△ABE中,AE===4.
22.【解答】证明:(1)∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
在△BOE和△AOF中,
∵,
∴△BOE≌△AOF.
∴OE=OF.
(2)OE=OF成立.
∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,
∠E+∠OBE=90°,
又∵∠MBF=∠OBE,
∴∠F=∠E.
在△BOE和△AOF中,
∵,
∴△BOE≌△AOF.
∴OE=OF.
23.【解答】解:(1)∵AB=BA,AC=BD,
∴Rt△ABC≌Rt△BAD(HL).
(2)∵AH∥GB,BH∥GA,
∴四边形AHBG是平行四边形.
∵△ABC≌△BAD,
∴∠ABD=∠BAC,
∴GA=GB,
∴平行四边形AHBG是菱形.
(3)∵AB=BC,∠ABC=90°,
∴△ABC是等腰直角三角形,
∴∠BAG=45°,
又∵△ABC≌△BAD,
∴∠ABG=∠BAG=45°,
∴∠AGB=90°,
∴菱形AHBG是正方形.
24.【解答】(1)证明:∵DE=OC,DE∥AC,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)解:在菱形ABCD中,∠ABC=60°,
∴AC=AB=4,
∴在矩形OCED中,CE=OD==2,
∴在△ACE中,AE==2.
满分120分
班级:________姓名:________座位:________成绩:________
一.选择题(共10小题,满分30分)
1.检查一个门框(已知两组对边分别相等)是不是矩形,不可用的方法是( )
A.测量两条对角线是否相等
B.用重锤线检查竖门框是否与地面垂直
C.测量两条对角线是否互相平分
D.测量门框的三个角是否都是直角
2.如图,在菱形ABCD中,对角线AC,BD相交于点O.若∠BAD=50°,则∠CBD=( )
A.25° B.40° C.65° D.75°
3.如图,要使?ABCD成为菱形,则需添加的一个条件是( )
A.AC=AD B.BA=BC C.∠ABC=90° D.AC=BD
4.在矩形ABCD中,对角线AC=10cm,AB:BC=4:3,则它的周长为( )cm.
A.14 B.20 C.28 D.30
5.如图,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是( )
A.6 B.12 C.24 D.48
6.如图,在矩形ABCD中,AB=4,BC=6,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE的长是( )
A.1 B. C.2 D.
7.如图,在一张长方形纸片上画一条线段AB,将右侧部分纸片四边形ABCD沿线段AB翻折至四边形ABC'D',若∠ABC=58°,则∠1=( )
A.60° B.64° C.42° D.52°
8.如图,点E为正方形ABCD内一点,AD=ED,∠AED=70°,连结EC,那么∠AEC的度数是( )
A.105° B.130° C.135° D.140°
9.如图,四边形ABCD是菱形,DH⊥AB于H,若AC=8,BD=6,则DH的长度为( )
A.2.4 B.3.6 C.4.8 D.7.2
10.如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=DG;③∠CHG=∠DAG;④2HG=AD.正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,满分18分)
11.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,若矩形ABCD的面积是12,那么阴影部分的面积是 .
12.如图,四边形ABCD中,对角线AC,BD相等且互相平分,再添加一个条件,使得四边形ABCD是正方形,可添加的条件是 .(写出一个条件即可)
13.如图,矩形ABCD中,直线MN垂直平分AC,与CD,AB分别交于点M,N.若DM=2,CM=3,则矩形的对角线AC的长为 .
14.如图,已知菱形ABCD的边长为2,∠CDA=120°,则对角线AC的长为 .
15.如图,延长正方形ABCD的边BC至E,使CE=AC,则∠E= .
16.如图,正方形ABCD的边长为10,点M在AD上,AM=8,过M作MN∥AB,分别交AC、BC于H、N两点,若E、F分别为CH、BM的中点,则EF的长为 .
三.解答题(共8小题,满分72分)
17.如图,在矩形ABCD中,点E是CD边上的中点.求证:AE=BE.
18.如图,在菱形ABCD中,过点B作BE⊥AD于E,过点B作BF⊥CD于F,求证:AE=CF.
19.如图,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC,交BC于F,试说明EC=EF=BF.
20.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD,
(1)求证:四边形OCED是菱形;
(2)若∠E=60°,DE=2,求矩形ABCD的面积.
21.如图,在四边形ABCD中,AD∥BC,∠D=90°,E为边BC上一点,且EC=AD,
连结AC.
(1)求证:四边形AECD是矩形;
(2)若AC平分∠DAB,AB=5,EC=2,求AE的长,
22.如图(1),正方形ABCD的对角线AC,BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM与BD相交于点F.
(1)求证:OE=OF;
(2)如图2若点E在AC的延长线上,AM⊥BE于点M,AM交DB的延长线于点F,其他条件不变,结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
23.在Rt△ABC与Rt△ABD中,∠ABC=∠BAD=90°,AC=BD,AC、BD相交于点G,过点A作AE∥DB交CB的延长线于点E,过点B作BF∥CA交DA的延长线于点F,AE、BF相交于点H.
(1)证明:△ABD≌△BAC.
(2)证明:四边形AHBG是菱形.
(3)若AB=BC,证明四边形AHBG是正方形.
24.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=OC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为4,∠ABC=60°,求AE的长.
参考答案
一.选择题(共10小题)
1.【解答】解:∵门框两组对边分别相等,
∴门框是个平行四边形,
∵对角线相等的平行四边形是矩形,
故A不符合题意;
∵竖门框与地面垂直,门框一定是矩形;
故B不符合题意,
∵对角线互相平分的四边形是平行四边形,
∴C符合题意,
∵三个角都是直角的四边形是矩形,
故D不符合题意;
故选:C.
2.【解答】解:∵四边形ABCD为菱形,
∴∠DAB+∠ABC=180°,BD平分∠ABC,
∵∠BAD=50°,
∴∠ABC=130°,
∴∠CBD=∠ABC=65°,
故选:C.
3.【解答】解:邻边相等的平行四边形为菱形.如图,要使?ABCD成为菱形,则需添加的一个条件是BA=BC.
故选:B.
4.【解答】解:设AB=4xcm,则BC=3xcm,
∵四边形ABCD是矩形,
∴∠B=90°,AB=CD,AD=BC,
∴AC===5x(cm),
∴5x=10cm,
∴x=2cm,
∴AB=8cm,BC=6cm,
∴矩形ABCD的周长=2(8+6)=28(cm),
故选:C.
5.【解答】解:∵菱形ABCD的周长是20,
∴AB=20÷4=5,AC⊥BD,OB=BD=3,
∴OA==4,
∴AC=2OA=8,
∴菱形ABCD的面积是:AC?BD=×8×6=24.
故选:C.
6.【解答】解:连接CE,如图所示:
∵四边形ABCD是矩形,
∴∠ADC=90°,CD=AB=4,AD=BC=6,OA=OC,
∵EF⊥AC,
∴AE=CE,
设DE=x,则CE=AE=6﹣x,
在Rt△CDE中,由勾股定理得:x2+42=(6﹣x)2,
解得:x=,
即DE=;
故选:D.
7.【解答】解:∵AD∥BC,
∴∠ABC+∠BAD=180°,且∠ABC=58°,
∴∠BAD=122°,
∵将右侧部分纸片四边形ABCD沿线段AB翻折至四边形ABC'D',
∴∠BAD=∠BAD'=122°,
∴∠1=122°+122°﹣180°=64°,
故选:B.
8.【解答】解:∵AD=DE,
∴∠DAE=∠AED=70°,
∴∠ADE=180°﹣70°﹣70°=40°,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠EDC=50°,
∴DC=DE,
∴∠DEC=∠DCE=(180°﹣50°)=65°,
∴∠AEC=∠AED+∠DEC=135°,
故选:C.
9.【解答】解:设AC与BD的交点为O,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=4,OB=OD=3,
∴AB=5,
∴S菱形ABCD=AC?BD=AB?DH,
∴DH==4.8.
故选:C.
10.【解答】解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=90°,
∵点E、F、H分别是AB、BC、CD的中点,
∴BE=CF,
在△BCE与△CDF中,,
∴△BCE≌△CDF,(SAS),
∴∠ECB=∠CDF,
∵∠BCE+∠ECD=90°,
∴∠ECD+∠CDF=90°,
∴∠CGD=90°,
∴CE⊥DF;故①正确;
在Rt△CGD中,H是CD边的中点,
∴HG=CD=AD,
即2HG=AD;故④正确;
连接AH,如图所示:
同理可得:AH⊥DF,
∵HG=HD=CD,
∴DK=GK,
∴AH垂直平分DG,
∴AG=AD;
若AG=DG,则△ADG是等边三角形,
则∠ADG=60°,∠CDF=30°,
而CF=CD≠DF,
∴∠CDF≠30°,
∴∠ADG≠60°,
∴AG≠DG,故②错误;
∴∠DAG=2∠DAH,
同理:△ADH≌△DCF,
∴∠DAH=∠CDF,
∵GH=DH,
∴∠HDG=∠HGD,
∴∠GHC=∠HDG+∠HGD=2∠CDF,
∴∠CHG=∠DAG;故③正确;
正确的结论有3个,
故选:C.
二.填空题(共6小题)
11.【解答】解:∵四边形ABCD是矩形,
∴AB∥CD,OA=OC,
∴∠EAO=∠FCO,
在△AOE和△COF中,,
∴△AOE≌△COF(ASA),
∴S△AOE=S△COF,
∴S阴=S△COD=S矩形ABCD=3,
故答案为:3.
12.【解答】解:∵对角线AC与BD互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD为矩形,
需添加一个条件是:AB=BC,
∴四边形ABCD是正方形;答案不唯一,
故答案为:AB=BC.
13.【解答】解:如图,连接AM.
∵直线MN垂直平分AC,
∴MA=MC=3,
∵四边形ABCD是矩形,
∴∠D=90°,
∵DM=2,MA=3,
∴AD2=AM2﹣DM2=32﹣22=5,
∴AC===;
故答案为:.
14.【解答】解:连接BD交AC于O,如图,
∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC,AD=AB=2,
∴∠CDA=120°,
∴∠DAB=60°,
∴△ADB为等边三角形,
∴OA=AB=,
∴AC=2OA=2.
故答案为:2.
15.【解答】解:∵四边形ABCD是正方形,
∴∠ACB=45°,
∵AC=CE,
∴∠E=∠CAF,
∵∠ACB是△ACE的外角,
∴∠E=∠ACB=22.5°,
故答案为:22.5°.
16.【解答】解:过F作FG⊥BC于点G,过E作EP⊥BC于点P,EK⊥FG于点K交MN于点Q,如图所示:
∵四边形ABCD是正方形,
∴AD∥BC,BC=10,
∵MN∥AB,
∴四边形ABNM是矩形,
∴BN=AM=8,MN=10,
∴CN=2,
∵AC是正方形ABCD的对角线,
∴∠CHN=∠HCN=45°,
∴HN=CN=2,
∵E为CH的中点,EP⊥BC,
∴EP是△CHN的中位线,
∴EQ=EP=HN=1,CP=PN=CN=1,
∵F为BM的中点,FG⊥BC,
∴FG是△BMN的中位线,
∴FG=MN=5,BG=NG=BN=4,
∵EK⊥FG,∴四边形PEQN是正方形,四边形QKGN是矩形,
∴GK=EP=1,QK=NG=4,
∴EK=EQ+QK=5,FK=FG﹣GK=4,
在Rt△EFK中,EF===.
三.解答题(共8小题)
17.【解答】证明:∵四边形ABCD是矩形,
∴AD=BC,∠D=∠C=90°,
∵E为CD边上的中点,
∴DE=CE,
∴△ADE≌△BCE(SAS),
∴AE=BE.
18.【解答】证明:∵菱形ABCD,
∴BA=BC,∠A=∠C,
∵BE⊥AD,BF⊥CD,
∴∠BEA=∠BFC=90°,
在△ABE与△CBF中
,
∴△ABE≌△CBF(AAS),
∴AE=CF.
19.【解答】解:在Rt△AEF和Rt△ABF中,
,
∴Rt△AEF≌Rt△ABF(HL),
∴FE=FB.
∵正方形ABCD,
∴∠ACB=∠BCD=45°,
在Rt△CEF中,
∵∠ACB=45°,
∴∠CFE=45°,
∴∠ACB=∠CFE,
∴EC=EF,
∴FB=EC=EF.
20.【解答】证明:(1)∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,
∴OC=OD,
∴四边形OCED是菱形;
(2)∵四边形OCED是菱形
∴OC=OD=DE=2,∠E=∠DOC=60°
∴BD=4,△OCD是等边三角形
∴CD=OC=2
∴BC==2
∴矩形ABCD的面积=BC×CD=4
21.【解答】解:(1)证明:∵AD∥BC,EC=AD,
∴四边形AECD是平行四边形.
又∵∠D=90°,
∴四边形AECD是矩形.
(2)∵AC平分∠DAB.
∴∠BAC=∠DAC.
∵AD∥BC,
∴∠DAC=∠ACB.
∴∠BAC=∠ACB.
∴BA=BC=5.
∵EC=2,
∴BE=3.
∴在Rt△ABE中,AE===4.
22.【解答】证明:(1)∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
在△BOE和△AOF中,
∵,
∴△BOE≌△AOF.
∴OE=OF.
(2)OE=OF成立.
∵四边形ABCD是正方形,
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠F+∠MBF=90°,
∠E+∠OBE=90°,
又∵∠MBF=∠OBE,
∴∠F=∠E.
在△BOE和△AOF中,
∵,
∴△BOE≌△AOF.
∴OE=OF.
23.【解答】解:(1)∵AB=BA,AC=BD,
∴Rt△ABC≌Rt△BAD(HL).
(2)∵AH∥GB,BH∥GA,
∴四边形AHBG是平行四边形.
∵△ABC≌△BAD,
∴∠ABD=∠BAC,
∴GA=GB,
∴平行四边形AHBG是菱形.
(3)∵AB=BC,∠ABC=90°,
∴△ABC是等腰直角三角形,
∴∠BAG=45°,
又∵△ABC≌△BAD,
∴∠ABG=∠BAG=45°,
∴∠AGB=90°,
∴菱形AHBG是正方形.
24.【解答】(1)证明:∵DE=OC,DE∥AC,
∴四边形OCED是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)解:在菱形ABCD中,∠ABC=60°,
∴AC=AB=4,
∴在矩形OCED中,CE=OD==2,
∴在△ACE中,AE==2.
