人教版九年级数学下册:27.2.1相似三角形的判定同步练习(含答案)
文档属性
| 名称 | 人教版九年级数学下册:27.2.1相似三角形的判定同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 146.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 00:00:00 | ||
图片预览


文档简介
27.2.1相似三角形的判定
同步练习
选择题
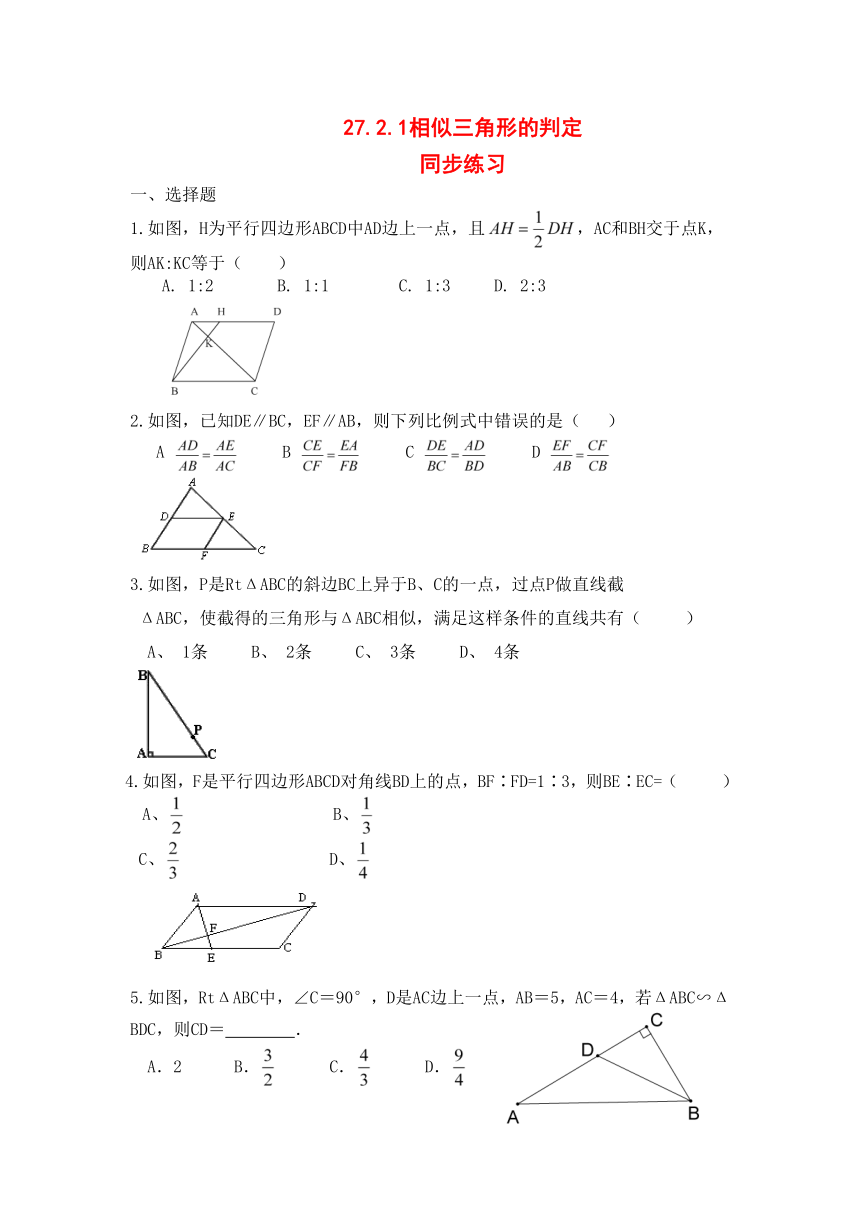
1.如图,H为平行四边形ABCD中AD边上一点,且,AC和BH交于点K,则AK:KC等于( )
A. 1:2 B. 1:1 C. 1:3 D. 2:3
2.如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
A B C D
3.如图,P是RtΔABC的斜边BC上异于B、C的一点,过点P做直线截
ΔABC,使截得的三角形与ΔABC相似,满足这样条件的直线共有( )
A、 1条 B、 2条 C、 3条 D、 4条
4.如图,F是平行四边形ABCD对角线BD上的点,BF∶FD=1∶3,则BE∶EC=( )
A、 B、
C、 D、
5.如图,RtΔABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若ΔABC∽ΔBDC,则CD= .
A.2 B. C. D.
6.如图,与交于点P,,,,,则( )
A. ab B. bd C. ae D. ce
7.下列命题中正确的是 ( )
①三边对应成比例的两个三角形相似
②二边对应成比例且一个角对应相等的两个三角形相似
③一个锐角对应相等的两个直角三角形相似
④一个角对应相等的两个等腰三角形相似
A、①③ B、①④ C、①②④ D、①③④
8.在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有( )
A ΔADE∽ΔAEF B ΔECF∽ΔAEF
C ΔADE∽ΔECF D ΔAEF∽ΔABF
9.如图,锐角的高CD和BE相交于点O,图中与相似的三角形有 ( )
A 4个 B 3个 C 2个 D 1个
10.、如图,D、E分别是AB、AC上两点,CD与BE相交于点O,
下列条件中不能使ΔABE和ΔACD相似的是 ( )
A. ∠B=∠C B. ∠ADC=∠AEB
C. BE=CD,AB=AC D. AD∶AC=AE∶AB
填空题
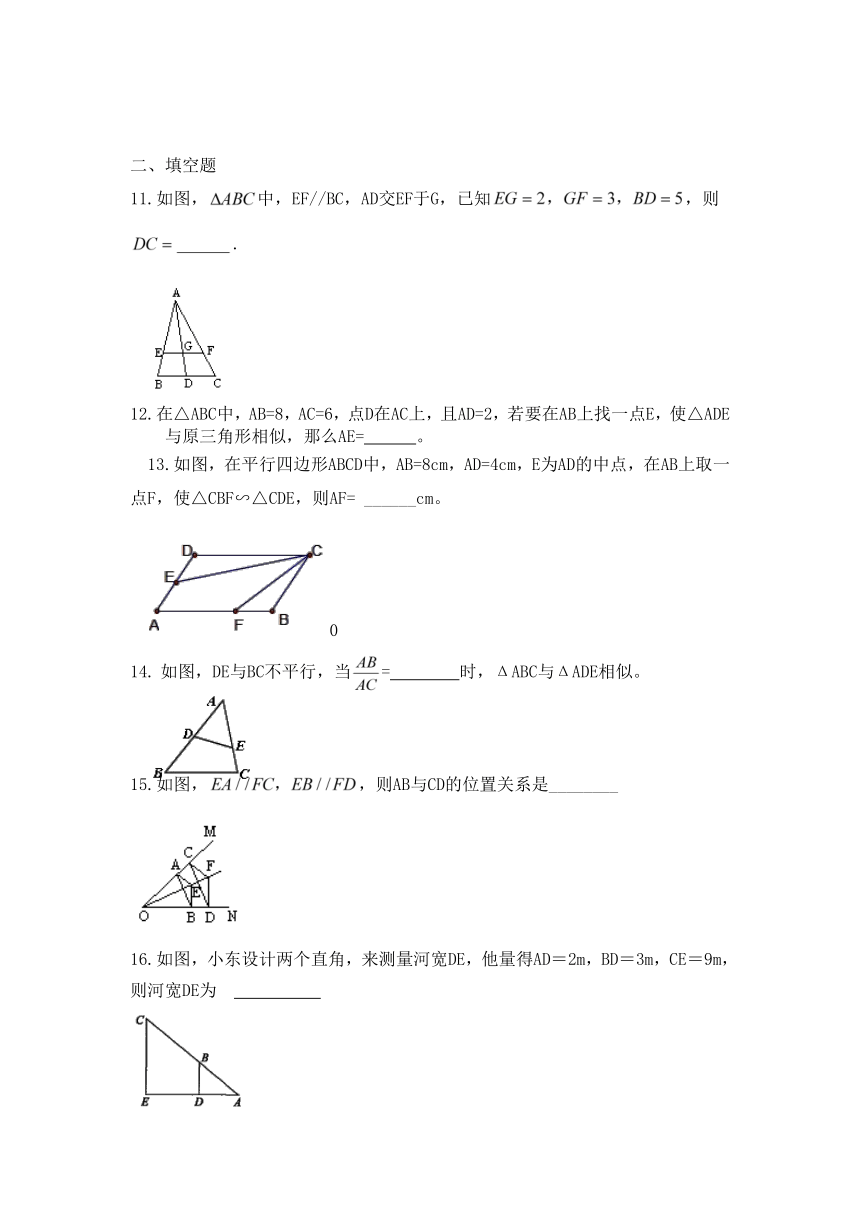
11.如图,中,EF//BC,AD交EF于G,已知,则.
12.在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,若要在AB上找一点E,使△ADE与原三角形相似,那么AE= 。
13.如图,在平行四边形ABCD中,AB=8cm,AD=4cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF= ______cm。
0
如图,DE与BC不平行,当= 时,ΔABC与ΔADE相似。
15.如图,,则AB与CD的位置关系是________
16.如图,小东设计两个直角,来测量河宽DE,他量得AD=2m,BD=3m,CE=9m,则河宽DE为
综合题
17.如图,中,AD是角平分线,交AB于E,已知,,求DE。
18.如图,ΔABC与ΔADB中,∠ABC=∠ADB=90°,AC=5cm,AB=4cm,如果图中的两个直角三角形相似,求AD的长.
19.如图,点C、D在线段AB上,且ΔPCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,ΔACP∽ΔPDB;
(2)当ΔPDB∽ΔACP时,试求∠APB的度数.
20.已知:如图,CE是RtΔABC的斜边AB上的高,BG⊥AP.
求证:CE2=ED·EP.
27.2.1 相似三角形的判定
同步测试
选择题
1.C 2.B 3.B 4.A 5.D 6.D 7.B 8.C 9.B 10.C
二、填空题
11.
12.
13.7
14.
15.平行
16.4
三、综合
17.解:
又平分,
18.解:。
19.(1)因为三角形PCD是等边三角形,所以CD=PC=PD
因为△ACP∽△PDB,所以AC/CP=PD/DB
所以AC/CD=CD/DB,即CD方=AC.DB
(2)因为△ACP∽△PDB,所以∠A=∠DPB
因为∠DPB+∠B+∠PDB=180,∠PDB=180-∠PDC=120
所以∠B+∠DPB=60
所以∠A+∠B=60,所以∠APB=120
20.证明:∵CE是Rt△ABC的斜边AB上的高,
∴△ACE∽△CBE,
∴,
即CE2=AE?BE.
∵CE是Rt△ABC的斜边AB上的高,BG⊥AP,
∴∠P+∠PAE=90°,∠DBE+∠PAE=90°,
∴∠P=∠DBE,
又∵∠AEP=∠DEB=90°,
∴△AEP∽△DEB;
∴
即AE?BE=ED?EP,
又∵CE2=AE?BE,
∴CE2=ED?EP.
同步练习
选择题
1.如图,H为平行四边形ABCD中AD边上一点,且,AC和BH交于点K,则AK:KC等于( )
A. 1:2 B. 1:1 C. 1:3 D. 2:3
2.如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
A B C D
3.如图,P是RtΔABC的斜边BC上异于B、C的一点,过点P做直线截
ΔABC,使截得的三角形与ΔABC相似,满足这样条件的直线共有( )
A、 1条 B、 2条 C、 3条 D、 4条
4.如图,F是平行四边形ABCD对角线BD上的点,BF∶FD=1∶3,则BE∶EC=( )
A、 B、
C、 D、
5.如图,RtΔABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若ΔABC∽ΔBDC,则CD= .
A.2 B. C. D.
6.如图,与交于点P,,,,,则( )
A. ab B. bd C. ae D. ce
7.下列命题中正确的是 ( )
①三边对应成比例的两个三角形相似
②二边对应成比例且一个角对应相等的两个三角形相似
③一个锐角对应相等的两个直角三角形相似
④一个角对应相等的两个等腰三角形相似
A、①③ B、①④ C、①②④ D、①③④
8.在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有( )
A ΔADE∽ΔAEF B ΔECF∽ΔAEF
C ΔADE∽ΔECF D ΔAEF∽ΔABF
9.如图,锐角的高CD和BE相交于点O,图中与相似的三角形有 ( )
A 4个 B 3个 C 2个 D 1个
10.、如图,D、E分别是AB、AC上两点,CD与BE相交于点O,
下列条件中不能使ΔABE和ΔACD相似的是 ( )
A. ∠B=∠C B. ∠ADC=∠AEB
C. BE=CD,AB=AC D. AD∶AC=AE∶AB
填空题
11.如图,中,EF//BC,AD交EF于G,已知,则.
12.在△ABC中,AB=8,AC=6,点D在AC上,且AD=2,若要在AB上找一点E,使△ADE与原三角形相似,那么AE= 。
13.如图,在平行四边形ABCD中,AB=8cm,AD=4cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF= ______cm。
0
如图,DE与BC不平行,当= 时,ΔABC与ΔADE相似。
15.如图,,则AB与CD的位置关系是________
16.如图,小东设计两个直角,来测量河宽DE,他量得AD=2m,BD=3m,CE=9m,则河宽DE为
综合题
17.如图,中,AD是角平分线,交AB于E,已知,,求DE。
18.如图,ΔABC与ΔADB中,∠ABC=∠ADB=90°,AC=5cm,AB=4cm,如果图中的两个直角三角形相似,求AD的长.
19.如图,点C、D在线段AB上,且ΔPCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,ΔACP∽ΔPDB;
(2)当ΔPDB∽ΔACP时,试求∠APB的度数.
20.已知:如图,CE是RtΔABC的斜边AB上的高,BG⊥AP.
求证:CE2=ED·EP.
27.2.1 相似三角形的判定
同步测试
选择题
1.C 2.B 3.B 4.A 5.D 6.D 7.B 8.C 9.B 10.C
二、填空题
11.
12.
13.7
14.
15.平行
16.4
三、综合
17.解:
又平分,
18.解:。
19.(1)因为三角形PCD是等边三角形,所以CD=PC=PD
因为△ACP∽△PDB,所以AC/CP=PD/DB
所以AC/CD=CD/DB,即CD方=AC.DB
(2)因为△ACP∽△PDB,所以∠A=∠DPB
因为∠DPB+∠B+∠PDB=180,∠PDB=180-∠PDC=120
所以∠B+∠DPB=60
所以∠A+∠B=60,所以∠APB=120
20.证明:∵CE是Rt△ABC的斜边AB上的高,
∴△ACE∽△CBE,
∴,
即CE2=AE?BE.
∵CE是Rt△ABC的斜边AB上的高,BG⊥AP,
∴∠P+∠PAE=90°,∠DBE+∠PAE=90°,
∴∠P=∠DBE,
又∵∠AEP=∠DEB=90°,
∴△AEP∽△DEB;
∴
即AE?BE=ED?EP,
又∵CE2=AE?BE,
∴CE2=ED?EP.
