北师大版八年级下册:3.1 《图形的平移》同步练习(含答案)
文档属性
| 名称 | 北师大版八年级下册:3.1 《图形的平移》同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 155.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 21:32:51 | ||
图片预览

文档简介
3.1 图形的平移
一.选择题(共10小题)
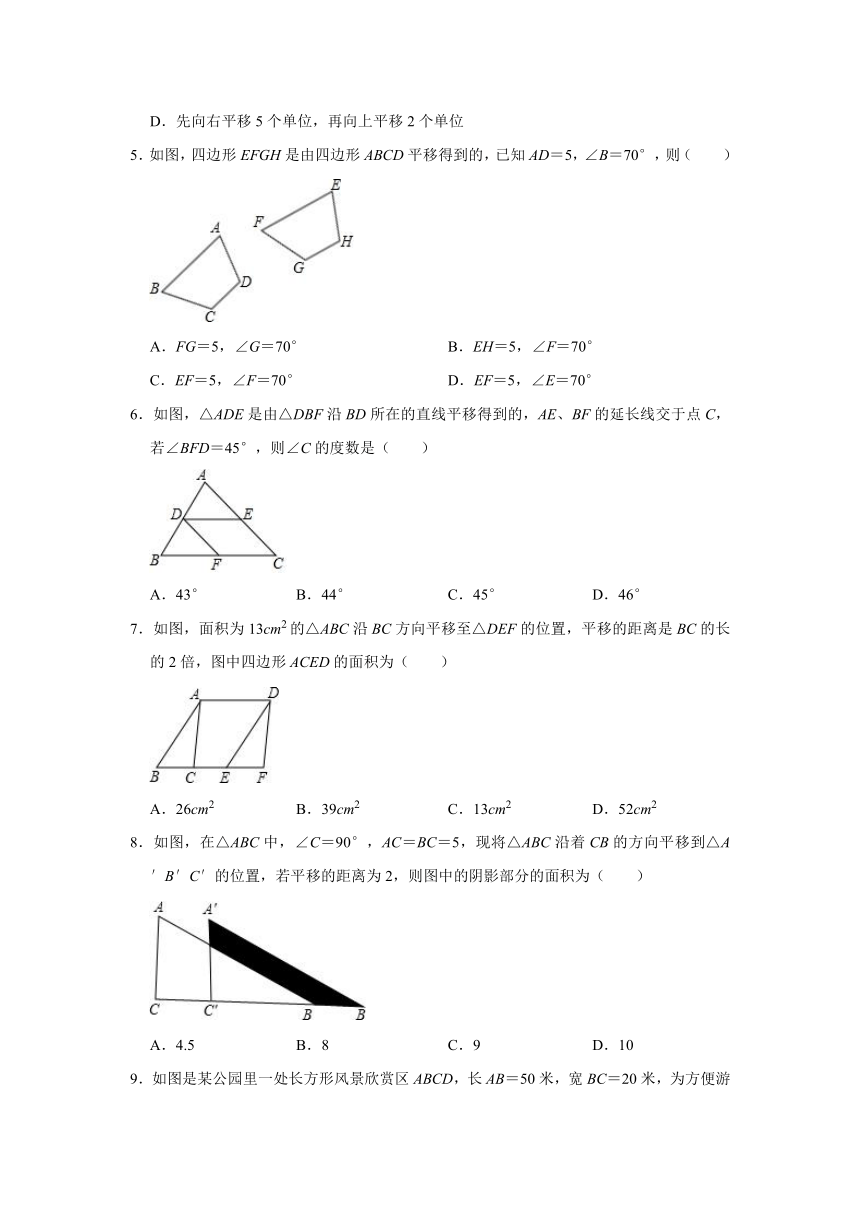
1.如图,哪一个选项的右边图形可由左边图形平移得到( )
A. B. C. D.
2.将如图所示的图案通过平移后可以得到的图案是( )
A. B. C. D.
3.在6×6方格中,将图1中的图形N平移后位置如图2所示,则图形N的平移方法中,正确的是( )
A.向下移动1格 B.向上移动1格
C.向上移动2格 D.向下移动2格
4.如图,在10×6的网格中,每个小正方形的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
A.先向右平移5个单位,再向下平移2个单位
B.先向左平移5个单位,再向下平移2个单位
C.先向左平移5个单位,再向上平移2个单位
D.先向右平移5个单位,再向上平移2个单位
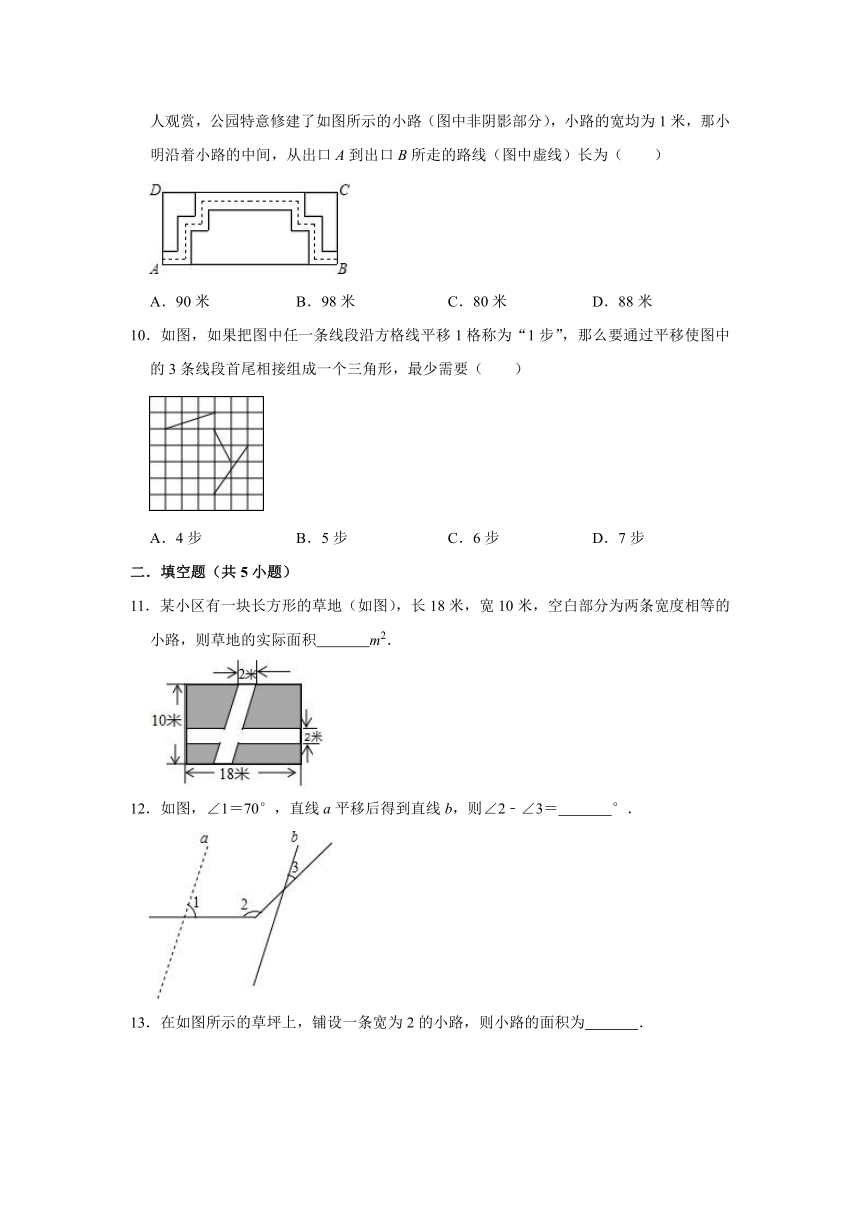
5.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
A.FG=5,∠G=70° B.EH=5,∠F=70°
C.EF=5,∠F=70° D.EF=5,∠E=70°
6.如图,△ADE是由△DBF沿BD所在的直线平移得到的,AE、BF的延长线交于点C,若∠BFD=45°,则∠C的度数是( )
A.43° B.44° C.45° D.46°
7.如图,面积为13cm2的△ABC沿BC方向平移至△DEF的位置,平移的距离是BC的长的2倍,图中四边形ACED的面积为( )
A.26cm2 B.39cm2 C.13cm2 D.52cm2
8.如图,在△ABC中,∠C=90°,AC=BC=5,现将△ABC沿着CB的方向平移到△A′B′C′的位置,若平移的距离为2,则图中的阴影部分的面积为( )
A.4.5 B.8 C.9 D.10
9.如图是某公园里一处长方形风景欣赏区ABCD,长AB=50米,宽BC=20米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
A.90米 B.98米 C.80米 D.88米
10.如图,如果把图中任一条线段沿方格线平移1格称为“1步”,那么要通过平移使图中的3条线段首尾相接组成一个三角形,最少需要( )
A.4步 B.5步 C.6步 D.7步
二.填空题(共5小题)
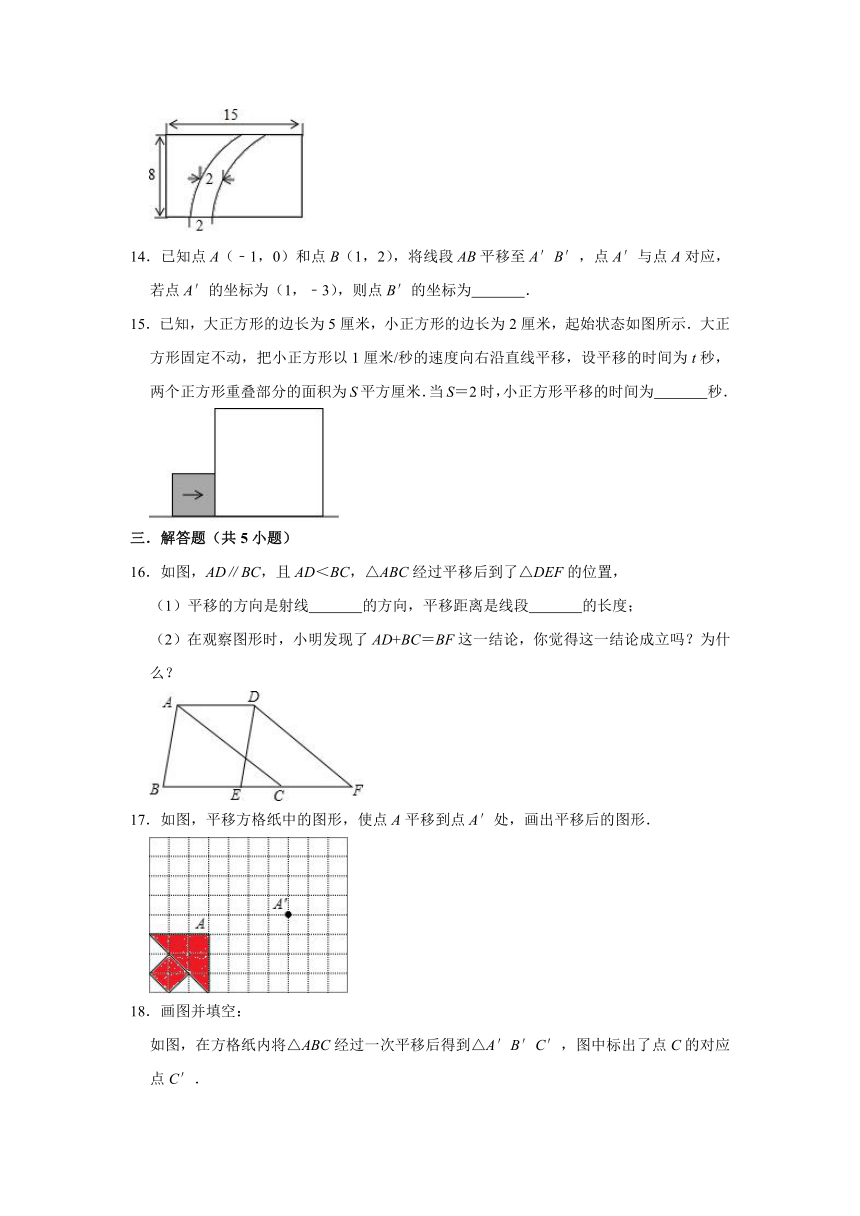
11.某小区有一块长方形的草地(如图),长18米,宽10米,空白部分为两条宽度相等的小路,则草地的实际面积 m2.
12.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3= °.
13.在如图所示的草坪上,铺设一条宽为2的小路,则小路的面积为 .
14.已知点A(﹣1,0)和点B(1,2),将线段AB平移至A′B′,点A′与点A对应,若点A′的坐标为(1,﹣3),则点B′的坐标为 .
15.已知,大正方形的边长为5厘米,小正方形的边长为2厘米,起始状态如图所示.大正方形固定不动,把小正方形以1厘米/秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,小正方形平移的时间为 秒.
三.解答题(共5小题)
16.如图,AD∥BC,且AD<BC,△ABC经过平移后到了△DEF的位置,
(1)平移的方向是射线 的方向,平移距离是线段 的长度;
(2)在观察图形时,小明发现了AD+BC=BF这一结论,你觉得这一结论成立吗?为什么?
17.如图,平移方格纸中的图形,使点A平移到点A′处,画出平移后的图形.
18.画图并填空:
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.
(1)画出平移后的△A′B′C′,(利用网格点和三角板画图)
(2)画出AB边上的中线CD;
(3)画出AC边上的高线BE;
(4)在平移过程中高BE扫过的面积为 .(网格中,每一小格单位长度为1).
19.平移△ABC,使得边AB移到DE的位置,如图是小刚的作业,他的作法完全正确.可由于一不小心将一团墨汁沾染到了作业本上,请设法帮小刚补全平移前后的△ABC和△DEF.
20.如图,粗线A→C→B和细线A→D→E→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.
(1)判断两条线的长短;
(2)小丽坐出租车由体育馆B到少年宫A,架设出租车的收费标准为:起步价为7元,3千米以后每千米1.8元,用代数式表示出租车的收费m元与行驶路程s(s>3)千米之间的关系;
(3)如果(2)中的这段路程长5千米,小丽身上有10元钱,够不够小丽坐出租车由体育馆到少年宫呢?说明理由.
参考答案
一.选择题(共10小题)
1. C.2.A.3. D.4.A.5. B.6. C.7. B.8. B.9. D.10. B.
二.填空题(共5小题)
11.
128.
12.
110.
13.
16.
14.
(3,﹣1).
15.
1或6.
三.解答题(共5小题)
16.解:(1)平移的方向是射线BC的方向,平移距离是线段BE或CF的长度;
(2)结论正确;
∵△ABC经过平移后到了△DEF的位置,
∴AD=BE=CF,BC=EF,
∴AD+BC=BE+EF=BF.
17.解:
18.解:(1)如图,△A′B′C′即为所求;
(2)如图,CD即为AB边上的中线;
(3)如图,BE就是所求的高;
(4)平移过程中高BE扫过的面积=4×6﹣2××2×4=24﹣8=16.
故答案为:16.
19.解:如图所示:
20.解:(1)如图所示:
根据平移可得:粗线A→C→B和细线A→D→E→F→G→H→B的长相等;
(2)根据题意得:m=7+1.8(s﹣3)=(1.8s+1.6)(元);
(3)当s=5时,m=7+1.8×(5﹣3)=10.6>10,
∴小丽不能坐出租车由体育馆到少年宫.
一.选择题(共10小题)
1.如图,哪一个选项的右边图形可由左边图形平移得到( )
A. B. C. D.
2.将如图所示的图案通过平移后可以得到的图案是( )
A. B. C. D.
3.在6×6方格中,将图1中的图形N平移后位置如图2所示,则图形N的平移方法中,正确的是( )
A.向下移动1格 B.向上移动1格
C.向上移动2格 D.向下移动2格
4.如图,在10×6的网格中,每个小正方形的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
A.先向右平移5个单位,再向下平移2个单位
B.先向左平移5个单位,再向下平移2个单位
C.先向左平移5个单位,再向上平移2个单位
D.先向右平移5个单位,再向上平移2个单位
5.如图,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
A.FG=5,∠G=70° B.EH=5,∠F=70°
C.EF=5,∠F=70° D.EF=5,∠E=70°
6.如图,△ADE是由△DBF沿BD所在的直线平移得到的,AE、BF的延长线交于点C,若∠BFD=45°,则∠C的度数是( )
A.43° B.44° C.45° D.46°
7.如图,面积为13cm2的△ABC沿BC方向平移至△DEF的位置,平移的距离是BC的长的2倍,图中四边形ACED的面积为( )
A.26cm2 B.39cm2 C.13cm2 D.52cm2
8.如图,在△ABC中,∠C=90°,AC=BC=5,现将△ABC沿着CB的方向平移到△A′B′C′的位置,若平移的距离为2,则图中的阴影部分的面积为( )
A.4.5 B.8 C.9 D.10
9.如图是某公园里一处长方形风景欣赏区ABCD,长AB=50米,宽BC=20米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
A.90米 B.98米 C.80米 D.88米
10.如图,如果把图中任一条线段沿方格线平移1格称为“1步”,那么要通过平移使图中的3条线段首尾相接组成一个三角形,最少需要( )
A.4步 B.5步 C.6步 D.7步
二.填空题(共5小题)
11.某小区有一块长方形的草地(如图),长18米,宽10米,空白部分为两条宽度相等的小路,则草地的实际面积 m2.
12.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3= °.
13.在如图所示的草坪上,铺设一条宽为2的小路,则小路的面积为 .
14.已知点A(﹣1,0)和点B(1,2),将线段AB平移至A′B′,点A′与点A对应,若点A′的坐标为(1,﹣3),则点B′的坐标为 .
15.已知,大正方形的边长为5厘米,小正方形的边长为2厘米,起始状态如图所示.大正方形固定不动,把小正方形以1厘米/秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,小正方形平移的时间为 秒.
三.解答题(共5小题)
16.如图,AD∥BC,且AD<BC,△ABC经过平移后到了△DEF的位置,
(1)平移的方向是射线 的方向,平移距离是线段 的长度;
(2)在观察图形时,小明发现了AD+BC=BF这一结论,你觉得这一结论成立吗?为什么?
17.如图,平移方格纸中的图形,使点A平移到点A′处,画出平移后的图形.
18.画图并填空:
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.
(1)画出平移后的△A′B′C′,(利用网格点和三角板画图)
(2)画出AB边上的中线CD;
(3)画出AC边上的高线BE;
(4)在平移过程中高BE扫过的面积为 .(网格中,每一小格单位长度为1).
19.平移△ABC,使得边AB移到DE的位置,如图是小刚的作业,他的作法完全正确.可由于一不小心将一团墨汁沾染到了作业本上,请设法帮小刚补全平移前后的△ABC和△DEF.
20.如图,粗线A→C→B和细线A→D→E→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.
(1)判断两条线的长短;
(2)小丽坐出租车由体育馆B到少年宫A,架设出租车的收费标准为:起步价为7元,3千米以后每千米1.8元,用代数式表示出租车的收费m元与行驶路程s(s>3)千米之间的关系;
(3)如果(2)中的这段路程长5千米,小丽身上有10元钱,够不够小丽坐出租车由体育馆到少年宫呢?说明理由.
参考答案
一.选择题(共10小题)
1. C.2.A.3. D.4.A.5. B.6. C.7. B.8. B.9. D.10. B.
二.填空题(共5小题)
11.
128.
12.
110.
13.
16.
14.
(3,﹣1).
15.
1或6.
三.解答题(共5小题)
16.解:(1)平移的方向是射线BC的方向,平移距离是线段BE或CF的长度;
(2)结论正确;
∵△ABC经过平移后到了△DEF的位置,
∴AD=BE=CF,BC=EF,
∴AD+BC=BE+EF=BF.
17.解:
18.解:(1)如图,△A′B′C′即为所求;
(2)如图,CD即为AB边上的中线;
(3)如图,BE就是所求的高;
(4)平移过程中高BE扫过的面积=4×6﹣2××2×4=24﹣8=16.
故答案为:16.
19.解:如图所示:
20.解:(1)如图所示:
根据平移可得:粗线A→C→B和细线A→D→E→F→G→H→B的长相等;
(2)根据题意得:m=7+1.8(s﹣3)=(1.8s+1.6)(元);
(3)当s=5时,m=7+1.8×(5﹣3)=10.6>10,
∴小丽不能坐出租车由体育馆到少年宫.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
