北师大版八年级数学下学期:3.2 图形的旋转 同步练习(含答案)
文档属性
| 名称 | 北师大版八年级数学下学期:3.2 图形的旋转 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 176.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 21:30:34 | ||
图片预览

文档简介
3.2 图形的旋转
一.选择题(共9小题)
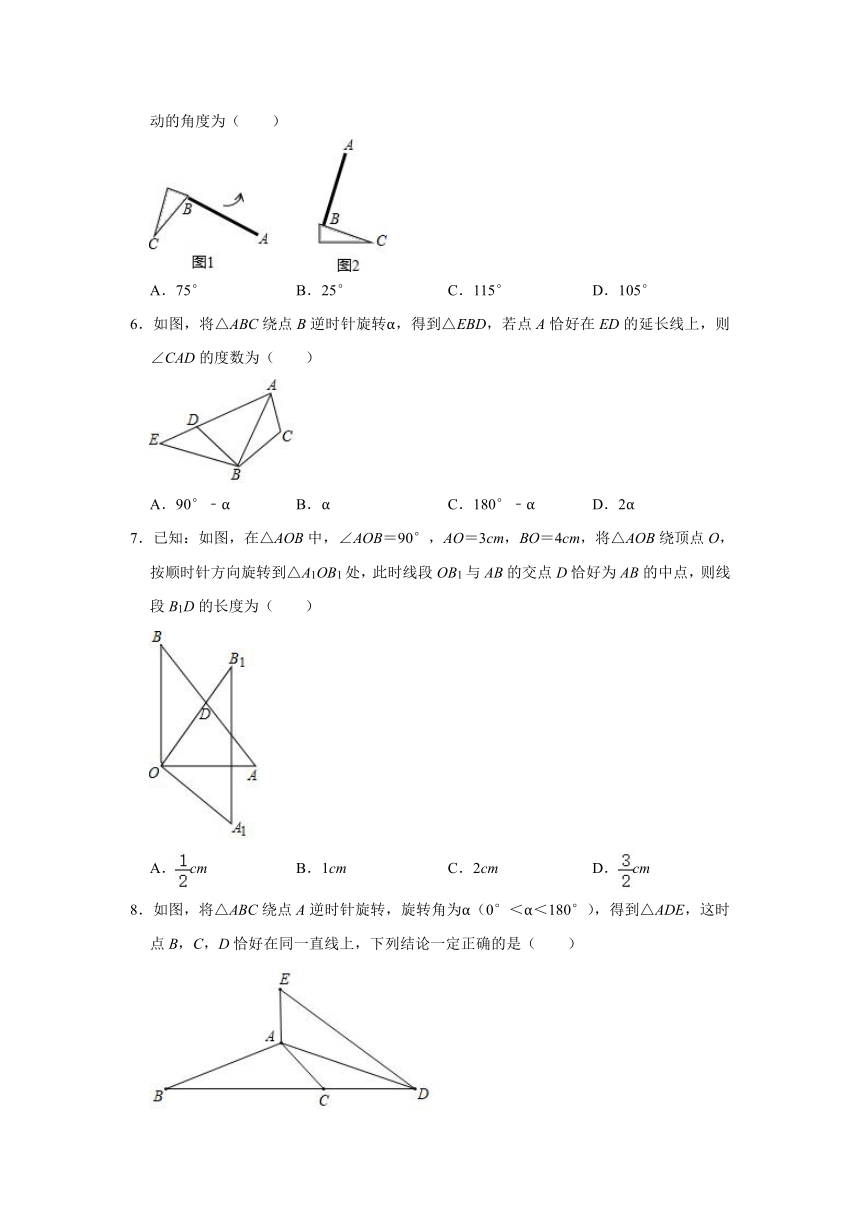
1.下列图形中,是轴对称图形但不是旋转对称图形的是( )
A. B.
C. D.
2.下列四个图形图案中,分别以它们所在圆的圆心为旋转中心,旋转一定角度后,能与原图形完全重合,其中,旋转角度最小的是( )
A. B. C. D.
3.如图所示,将一个含30°角的直角三角板ABC绕点A顺时针旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
A.60° B.90° C.120° D.150°
4.在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
A.点A B.点B C.点C D.点D
5.如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )
A.75° B.25° C.115° D.105°
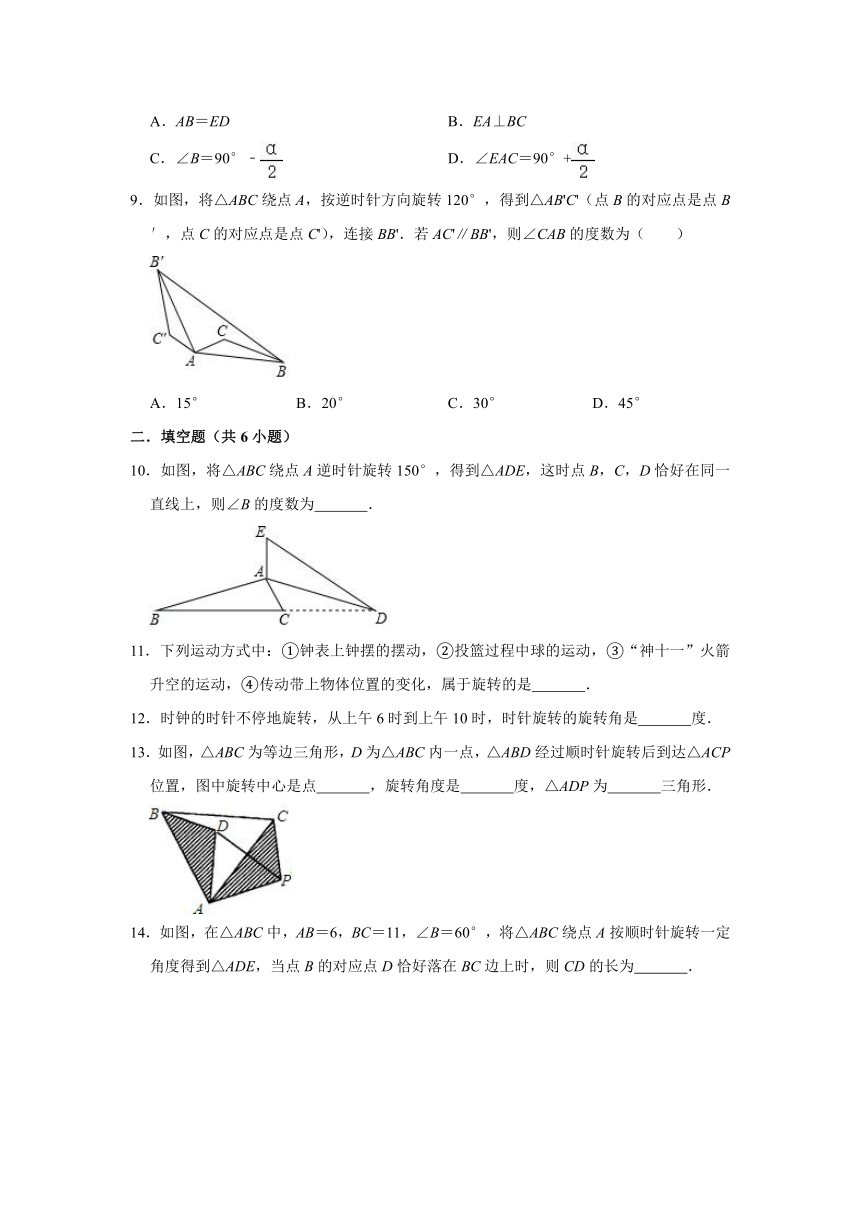
6.如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°﹣α B.α C.180°﹣α D.2α
7.已知:如图,在△AOB中,∠AOB=90°,AO=3cm,BO=4cm,将△AOB绕顶点O,按顺时针方向旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段B1D的长度为( )
A.cm B.1cm C.2cm D.cm
8.如图,将△ABC绕点A逆时针旋转,旋转角为α(0°<α<180°),得到△ADE,这时点B,C,D恰好在同一直线上,下列结论一定正确的是( )
A.AB=ED B.EA⊥BC
C.∠B=90°﹣ D.∠EAC=90°+
9.如图,将△ABC绕点A,按逆时针方向旋转120°,得到△AB'C'(点B的对应点是点B′,点C的对应点是点C'),连接BB'.若AC'∥BB',则∠CAB的度数为( )
A.15° B.20° C.30° D.45°
二.填空题(共6小题)
10.如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 .
11.下列运动方式中:①钟表上钟摆的摆动,②投篮过程中球的运动,③“神十一”火箭升空的运动,④传动带上物体位置的变化,属于旋转的是 .
12.时钟的时针不停地旋转,从上午6时到上午10时,时针旋转的旋转角是 度.
13.如图,△ABC为等边三角形,D为△ABC内一点,△ABD经过顺时针旋转后到达△ACP位置,图中旋转中心是点 ,旋转角度是 度,△ADP为 三角形.
14.如图,在△ABC中,AB=6,BC=11,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为 .
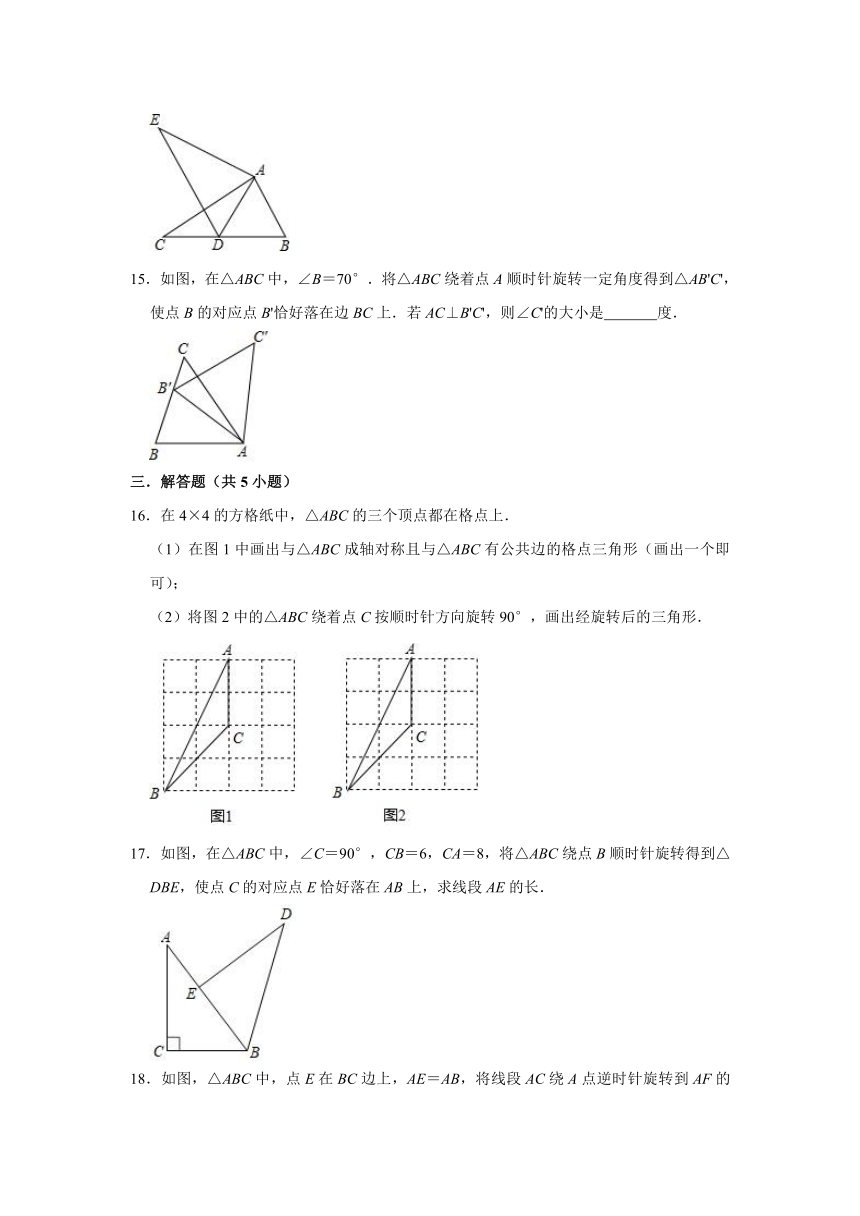
15.如图,在△ABC中,∠B=70°.将△ABC绕着点A顺时针旋转一定角度得到△AB'C',使点B的对应点B'恰好落在边BC上.若AC⊥B'C',则∠C'的大小是 度.
三.解答题(共5小题)
16.在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);
(2)将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.
17.如图,在△ABC中,∠C=90°,CB=6,CA=8,将△ABC绕点B顺时针旋转得到△DBE,使点C的对应点E恰好落在AB上,求线段AE的长.
18.如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点逆时针旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.求证:EF=BC.
19.(1)如图1,在△AEC和△DFB中,点A、B、C、D在同一条直线上,AE=DF,AE∥DF,∠E=∠F,求证:EC=BF.
(2)如图2,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,求旋转角的度数.
20.如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为 度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
参考答案
一.选择题(共9小题)
1.
B.
2.
D.
3.
D.
4.
B.
5.
D.
6.
C.
7.
D.
8.
C.
9.
C.
二.填空题(共6小题)
10.
15°.
11.
①.
12.
120.
13.
A,60,等边.
14.
5.
15.
50°.
三.解答题(共5小题)
16.解:如图所示.
17.解:∵在△ABC中,∠C=90°,CB=6,CA=8,
∴AB==10,
由旋转的性质得:BE=BC=6,
∴AE=AB﹣BE=10﹣6=4.
18.证明:∵∠CAF=∠BAE,
∴∠BAC=∠EAF,
∵将线段AC绕A点旋转到AF的位置,
∴AC=AF,
在△ABC与△AEF中,
,
∴△ABC≌△AEF(SAS),
∴EF=BC;
19.(1)证明:∵AE∥DF,
∴∠A=∠D,
在△AEC和△DFB中,
,
∴△AEC≌△DFB(ASA)
∴EC=BF
(2)∵CC′∥AB,
∴∠ACC′=∠CAB=55°,
∵△ABC绕点A旋转得到△AB′C′,
∴AC=AC′,
∴∠CAC′=180°﹣2∠ACC′=180°﹣2×55°=70°,
∴∠CAC′=∠BAB′=70°.
所以旋转角为70°
20.解:(1)由旋转的性质知,旋转角∠MON=90°.
故答案是:90;
(2)如图3,∠AOM﹣∠NOC=30°.
设∠AOC=α,由∠AOC:∠BOC=1:2可得
∠BOC=2α.
∵∠AOC+∠BOC=180°,
∴α+2α=180°.
解得 α=60°.
即∠AOC=60°.
∴∠AON+∠NOC=60°.①
∵∠MON=90°,
∴∠AOM+∠AON=90°.②
由②﹣①,得∠AOM﹣∠NOC=30°;
(3)(ⅰ)如图4,当直角边ON在∠AOC外部时,
由OD平分∠AOC,可得∠BON=30°.
因此三角板绕点O逆时针旋转60°.
此时三角板的运动时间为:
t=60°÷15°=4(秒).
(ⅱ)如图5,当直角边ON在∠AOC内部时,
由ON平分∠AOC,可得∠CON=30°.
因此三角板绕点O逆时针旋转240°.
此时三角板的运动时间为:
t=240°÷15°=16(秒).
一.选择题(共9小题)
1.下列图形中,是轴对称图形但不是旋转对称图形的是( )
A. B.
C. D.
2.下列四个图形图案中,分别以它们所在圆的圆心为旋转中心,旋转一定角度后,能与原图形完全重合,其中,旋转角度最小的是( )
A. B. C. D.
3.如图所示,将一个含30°角的直角三角板ABC绕点A顺时针旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
A.60° B.90° C.120° D.150°
4.在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
A.点A B.点B C.点C D.点D
5.如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )
A.75° B.25° C.115° D.105°
6.如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°﹣α B.α C.180°﹣α D.2α
7.已知:如图,在△AOB中,∠AOB=90°,AO=3cm,BO=4cm,将△AOB绕顶点O,按顺时针方向旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段B1D的长度为( )
A.cm B.1cm C.2cm D.cm
8.如图,将△ABC绕点A逆时针旋转,旋转角为α(0°<α<180°),得到△ADE,这时点B,C,D恰好在同一直线上,下列结论一定正确的是( )
A.AB=ED B.EA⊥BC
C.∠B=90°﹣ D.∠EAC=90°+
9.如图,将△ABC绕点A,按逆时针方向旋转120°,得到△AB'C'(点B的对应点是点B′,点C的对应点是点C'),连接BB'.若AC'∥BB',则∠CAB的度数为( )
A.15° B.20° C.30° D.45°
二.填空题(共6小题)
10.如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 .
11.下列运动方式中:①钟表上钟摆的摆动,②投篮过程中球的运动,③“神十一”火箭升空的运动,④传动带上物体位置的变化,属于旋转的是 .
12.时钟的时针不停地旋转,从上午6时到上午10时,时针旋转的旋转角是 度.
13.如图,△ABC为等边三角形,D为△ABC内一点,△ABD经过顺时针旋转后到达△ACP位置,图中旋转中心是点 ,旋转角度是 度,△ADP为 三角形.
14.如图,在△ABC中,AB=6,BC=11,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为 .
15.如图,在△ABC中,∠B=70°.将△ABC绕着点A顺时针旋转一定角度得到△AB'C',使点B的对应点B'恰好落在边BC上.若AC⊥B'C',则∠C'的大小是 度.
三.解答题(共5小题)
16.在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);
(2)将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.
17.如图,在△ABC中,∠C=90°,CB=6,CA=8,将△ABC绕点B顺时针旋转得到△DBE,使点C的对应点E恰好落在AB上,求线段AE的长.
18.如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点逆时针旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.求证:EF=BC.
19.(1)如图1,在△AEC和△DFB中,点A、B、C、D在同一条直线上,AE=DF,AE∥DF,∠E=∠F,求证:EC=BF.
(2)如图2,在△ABC中,∠CAB=55°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,求旋转角的度数.
20.如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为 度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值.
参考答案
一.选择题(共9小题)
1.
B.
2.
D.
3.
D.
4.
B.
5.
D.
6.
C.
7.
D.
8.
C.
9.
C.
二.填空题(共6小题)
10.
15°.
11.
①.
12.
120.
13.
A,60,等边.
14.
5.
15.
50°.
三.解答题(共5小题)
16.解:如图所示.
17.解:∵在△ABC中,∠C=90°,CB=6,CA=8,
∴AB==10,
由旋转的性质得:BE=BC=6,
∴AE=AB﹣BE=10﹣6=4.
18.证明:∵∠CAF=∠BAE,
∴∠BAC=∠EAF,
∵将线段AC绕A点旋转到AF的位置,
∴AC=AF,
在△ABC与△AEF中,
,
∴△ABC≌△AEF(SAS),
∴EF=BC;
19.(1)证明:∵AE∥DF,
∴∠A=∠D,
在△AEC和△DFB中,
,
∴△AEC≌△DFB(ASA)
∴EC=BF
(2)∵CC′∥AB,
∴∠ACC′=∠CAB=55°,
∵△ABC绕点A旋转得到△AB′C′,
∴AC=AC′,
∴∠CAC′=180°﹣2∠ACC′=180°﹣2×55°=70°,
∴∠CAC′=∠BAB′=70°.
所以旋转角为70°
20.解:(1)由旋转的性质知,旋转角∠MON=90°.
故答案是:90;
(2)如图3,∠AOM﹣∠NOC=30°.
设∠AOC=α,由∠AOC:∠BOC=1:2可得
∠BOC=2α.
∵∠AOC+∠BOC=180°,
∴α+2α=180°.
解得 α=60°.
即∠AOC=60°.
∴∠AON+∠NOC=60°.①
∵∠MON=90°,
∴∠AOM+∠AON=90°.②
由②﹣①,得∠AOM﹣∠NOC=30°;
(3)(ⅰ)如图4,当直角边ON在∠AOC外部时,
由OD平分∠AOC,可得∠BON=30°.
因此三角板绕点O逆时针旋转60°.
此时三角板的运动时间为:
t=60°÷15°=4(秒).
(ⅱ)如图5,当直角边ON在∠AOC内部时,
由ON平分∠AOC,可得∠CON=30°.
因此三角板绕点O逆时针旋转240°.
此时三角板的运动时间为:
t=240°÷15°=16(秒).
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
