北师大版八上数学第1章:1.3 勾股定理的应用习题课件(22张PPT)
文档属性
| 名称 | 北师大版八上数学第1章:1.3 勾股定理的应用习题课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 456.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 13:55:48 | ||
图片预览




文档简介
(共22张PPT)
3 勾股定理的应用
第一章 勾股定理
答案显示
A
C
C
约为18 cm
20
D
C
C
B
1 000 m
5 cm
5
24 s
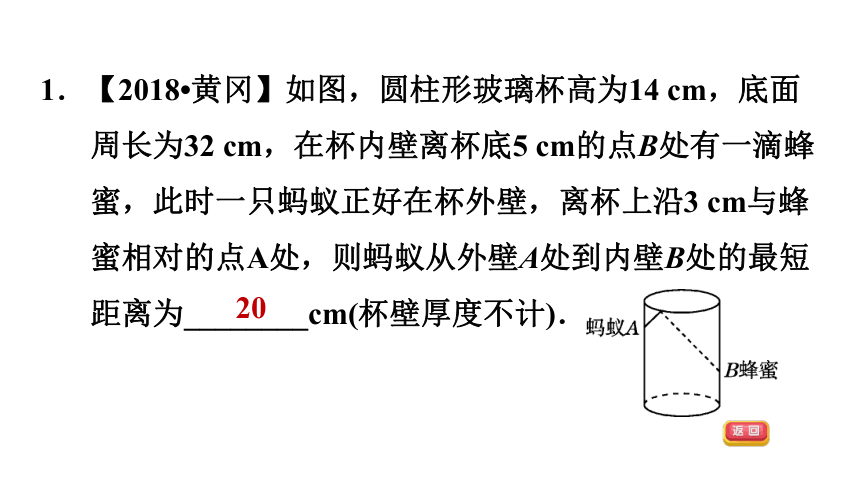
1.【2018?黄冈】如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为________cm(杯壁厚度不计).
20
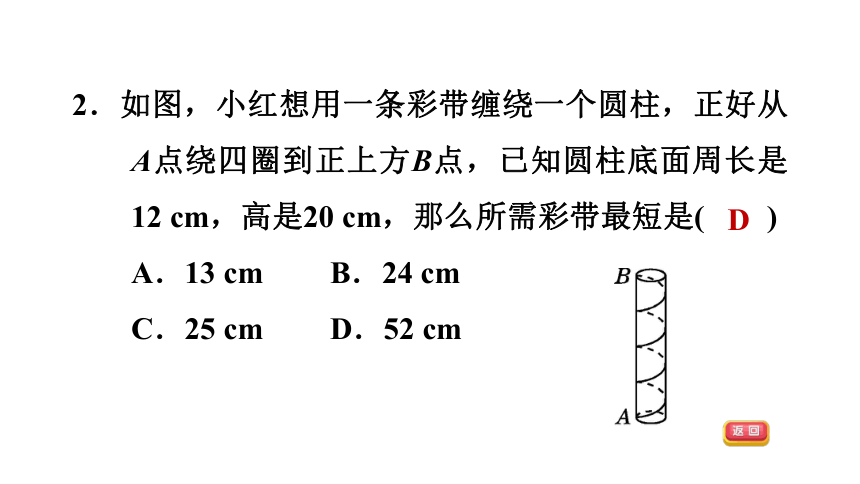
2.如图,小红想用一条彩带缠绕一个圆柱,正好从A点绕四圈到正上方B点,已知圆柱底面周长是12 cm,高是20 cm,那么所需彩带最短是( )
A.13 cm B.24 cm
C.25 cm D.52 cm
D
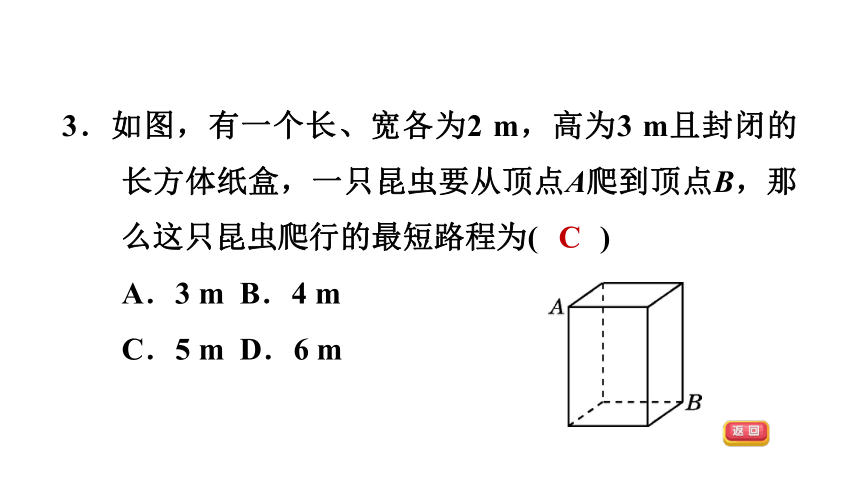
3.如图,有一个长、宽各为2 m,高为3 m且封闭的长方体纸盒,一只昆虫要从顶点A爬到顶点B,那么这只昆虫爬行的最短路程为( )
A.3 m B.4 m
C.5 m D.6 m
C
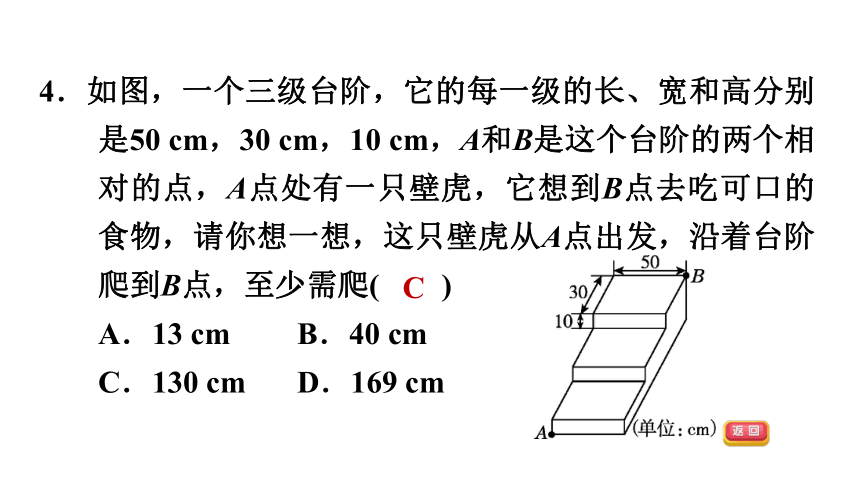
4.如图,一个三级台阶,它的每一级的长、宽和高分别是50 cm,30 cm,10 cm,A和B是这个台阶的两个相对的点,A点处有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶爬到B点,至少需爬( )
A.13 cm B.40 cm
C.130 cm D.169 cm
C
5.【2017·营口】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A.4 B.5 C.6 D.7
6.【2018·长沙】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米
C.75平方千米 D.750平方千米
A
7.如图,甲货船以16 n mile/h的速度从港口A出发向东北方向航行,乙货船以12 n mile/h的速度同时从港口A出发向东南方向航行,离开港口3 h时两船相距( )
A.35 n mile B.50 n mile
C.60 n mile D.40 n mile
C
8.如图,在长方形ABCD中,点E在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在BC边上的点F处,若AE=5,BF=3,则CD的长是( )
A.7 B.8
C.9 D.10
C
9.如图,有一个长方体纸盒,小明所在的数学合作小组研究长方体的底面A点到长方体与A相对的B点的表面最短距离.若长方体的长为12 cm,宽为9 cm,高为5 cm,请你帮助该小组求出A点到B点的表面最短距离(结果精确到1 cm.参考数据:21.592≈466,18.442≈340,19.242≈370).
解:将四边形ACDF与四边形FDBG在同一平面上展开,如图①所示,连接AB,在Rt△ACB中,
根据勾股定理,得AB2=AC2+BC2
=122+(5+9)2=340;
将四边形ACDF与四边形DCEB在同一平面上展开,如图②所示,连接AB,在Rt△AEB中,
根据勾股定理,得AB2=BE2+AE2
=52+(12+9)2=466;
将四边形AHGF与四边形FDBG在同一平面上展开,如图③所示,连接AB,在Rt△ADB中,
根据勾股定理,得AB2=AD2+BD2
=(5+12)2+92=370.
因为340<370<466,所以A点到B点的表面最短距离是如图①所示的情况.此时AB≈18 cm.故A点到B点的表面最短距离约为18 cm.
10.如图,已知长方体的长AC=2 cm,宽BC=1 cm,高AA′=4 cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么最短路程是多少?
解:根据题意,有以下三种情况:
(1)如图①,连接AB′,AB′2=AB2+BB′2=(2+1)2+42=25;
(2)如图②,
连接AB′,AB′2=AC2+B′C2=22+(4+1)2=4+25=29;
(3)如图③,连接AB′,AB′2=AD2+B′D2
=12+(4+2)2=1+36=37.
综上所述,最短路程应为如图①所示
的情况,此时AB′2=25,即AB′=5 cm.
故最短路程是5 cm.
11.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400 m,BD=200 m,CD=800 m,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少?
解:如图,作点A关于直线CD的对称点A′,连接A′B交CD于点M,连接AM,则AM=A′M,所以在点M处饮水所走的总路程最短,最短路程为A′B的长.
过点A′作A′H⊥BD交BD的延长线于点H.
在Rt△A′HB中,A′H=CD=800 m,
BH=BD+DH=BD+AC=200+400=600(m),由勾股定理,得A′B2=A′H2+BH2=8002+6002=1 000 000,故A′B=1 000 m,所以最短路程为1 000 m.
12.如图,在正方形ABCD中,AB边上有一点E,AE=3,EB=1,在AC上有一点P,使EP+BP最短.求EP+BP的最短长度.
解:如图,连接DE,与AC交于点P,连接BP,易知此时EP+BP最短,且最短长度为DE的长.
由题易知AD=AB=AE+EB=3+1=4.
所以DE2=AE2+AD2=32+42=25,
所以DE=5.
即EP+BP的最短长度为5.
13.如图,公路MN和公路PQ在点P处交会,公路PQ上点A处有一所学校,点A到公路MN的距离AB=80 m,现有一拖拉机在公路MN上以18 km/h的速度沿PN方向行驶,拖拉机行驶时周围100 m以内都会受到噪声的影响,则该校受影响的时间为多少秒?
解:如图,假设拖拉机行驶到C处,学校开始受到影响,连接AC,则AC=100 m.所以BC2=1002-802=602.所以BC=60 m.
假设拖拉机行驶到D处,学校开始脱离影响,连接AD,则AD=100 m,所以BD=60 m.
所以CD=120 m.
3 勾股定理的应用
第一章 勾股定理
答案显示
A
C
C
约为18 cm
20
D
C
C
B
1 000 m
5 cm
5
24 s
1.【2018?黄冈】如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为________cm(杯壁厚度不计).
20
2.如图,小红想用一条彩带缠绕一个圆柱,正好从A点绕四圈到正上方B点,已知圆柱底面周长是12 cm,高是20 cm,那么所需彩带最短是( )
A.13 cm B.24 cm
C.25 cm D.52 cm
D
3.如图,有一个长、宽各为2 m,高为3 m且封闭的长方体纸盒,一只昆虫要从顶点A爬到顶点B,那么这只昆虫爬行的最短路程为( )
A.3 m B.4 m
C.5 m D.6 m
C
4.如图,一个三级台阶,它的每一级的长、宽和高分别是50 cm,30 cm,10 cm,A和B是这个台阶的两个相对的点,A点处有一只壁虎,它想到B点去吃可口的食物,请你想一想,这只壁虎从A点出发,沿着台阶爬到B点,至少需爬( )
A.13 cm B.40 cm
C.130 cm D.169 cm
C
5.【2017·营口】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A.4 B.5 C.6 D.7
6.【2018·长沙】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米
C.75平方千米 D.750平方千米
A
7.如图,甲货船以16 n mile/h的速度从港口A出发向东北方向航行,乙货船以12 n mile/h的速度同时从港口A出发向东南方向航行,离开港口3 h时两船相距( )
A.35 n mile B.50 n mile
C.60 n mile D.40 n mile
C
8.如图,在长方形ABCD中,点E在边AB上,将长方形ABCD沿直线DE折叠,点A恰好落在BC边上的点F处,若AE=5,BF=3,则CD的长是( )
A.7 B.8
C.9 D.10
C
9.如图,有一个长方体纸盒,小明所在的数学合作小组研究长方体的底面A点到长方体与A相对的B点的表面最短距离.若长方体的长为12 cm,宽为9 cm,高为5 cm,请你帮助该小组求出A点到B点的表面最短距离(结果精确到1 cm.参考数据:21.592≈466,18.442≈340,19.242≈370).
解:将四边形ACDF与四边形FDBG在同一平面上展开,如图①所示,连接AB,在Rt△ACB中,
根据勾股定理,得AB2=AC2+BC2
=122+(5+9)2=340;
将四边形ACDF与四边形DCEB在同一平面上展开,如图②所示,连接AB,在Rt△AEB中,
根据勾股定理,得AB2=BE2+AE2
=52+(12+9)2=466;
将四边形AHGF与四边形FDBG在同一平面上展开,如图③所示,连接AB,在Rt△ADB中,
根据勾股定理,得AB2=AD2+BD2
=(5+12)2+92=370.
因为340<370<466,所以A点到B点的表面最短距离是如图①所示的情况.此时AB≈18 cm.故A点到B点的表面最短距离约为18 cm.
10.如图,已知长方体的长AC=2 cm,宽BC=1 cm,高AA′=4 cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么最短路程是多少?
解:根据题意,有以下三种情况:
(1)如图①,连接AB′,AB′2=AB2+BB′2=(2+1)2+42=25;
(2)如图②,
连接AB′,AB′2=AC2+B′C2=22+(4+1)2=4+25=29;
(3)如图③,连接AB′,AB′2=AD2+B′D2
=12+(4+2)2=1+36=37.
综上所述,最短路程应为如图①所示
的情况,此时AB′2=25,即AB′=5 cm.
故最短路程是5 cm.
11.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400 m,BD=200 m,CD=800 m,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少?
解:如图,作点A关于直线CD的对称点A′,连接A′B交CD于点M,连接AM,则AM=A′M,所以在点M处饮水所走的总路程最短,最短路程为A′B的长.
过点A′作A′H⊥BD交BD的延长线于点H.
在Rt△A′HB中,A′H=CD=800 m,
BH=BD+DH=BD+AC=200+400=600(m),由勾股定理,得A′B2=A′H2+BH2=8002+6002=1 000 000,故A′B=1 000 m,所以最短路程为1 000 m.
12.如图,在正方形ABCD中,AB边上有一点E,AE=3,EB=1,在AC上有一点P,使EP+BP最短.求EP+BP的最短长度.
解:如图,连接DE,与AC交于点P,连接BP,易知此时EP+BP最短,且最短长度为DE的长.
由题易知AD=AB=AE+EB=3+1=4.
所以DE2=AE2+AD2=32+42=25,
所以DE=5.
即EP+BP的最短长度为5.
13.如图,公路MN和公路PQ在点P处交会,公路PQ上点A处有一所学校,点A到公路MN的距离AB=80 m,现有一拖拉机在公路MN上以18 km/h的速度沿PN方向行驶,拖拉机行驶时周围100 m以内都会受到噪声的影响,则该校受影响的时间为多少秒?
解:如图,假设拖拉机行驶到C处,学校开始受到影响,连接AC,则AC=100 m.所以BC2=1002-802=602.所以BC=60 m.
假设拖拉机行驶到D处,学校开始脱离影响,连接AD,则AD=100 m,所以BD=60 m.
所以CD=120 m.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
