北师大版八上数学第1章勾股定理:全章热门考点整合应用课件(39张PPT)
文档属性
| 名称 | 北师大版八上数学第1章勾股定理:全章热门考点整合应用课件(39张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 866.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 14:01:51 | ||
图片预览










文档简介
(共39张PPT)
全章热门考点整合应用
第一章 勾股定理
答案显示
(64n2+36)cm2
1 300 m.
(1)AP=CQ.
(2)△PQC是直角三角形.
12
(1)n2-1;2n;n2+1
(2)直角三角形.
6cm2
(1)6;8;10;9;12;15(答案不唯一)
(2)是一组勾股数.
答案显示
170 cm
(1)AC=13. (2)60.
北偏东53°
(1)18cm2 (2)t=3
(3)t=6或10.8或12或13时
(1)AB=AP. (2)AC=6.
(3)∠AMP的大小不发生变化.
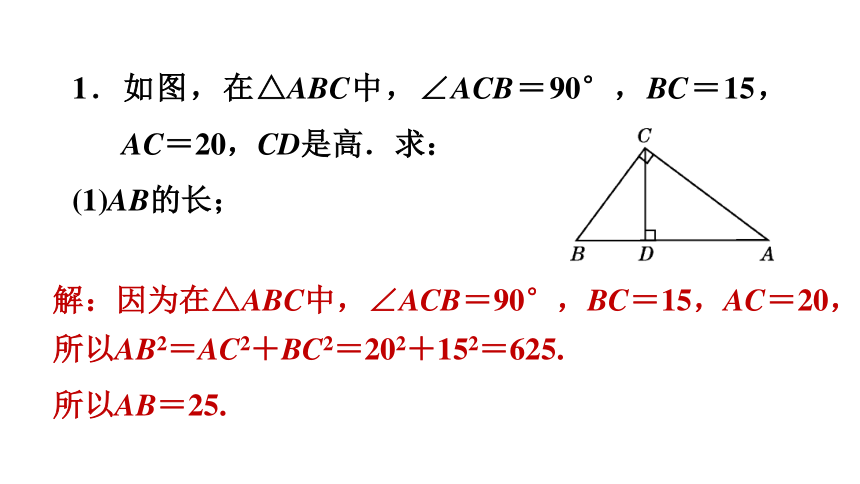
1.如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.求:
(1)AB的长;
解:因为在△ABC中,∠ACB=90°,BC=15,AC=20,
所以AB2=AC2+BC2=202+152=625.
所以AB=25.
1.如图,在△ABC中,∠ACB=90°,
BC=15,AC=20,CD是高.求:
(2)△ABC的面积;
(3)CD的长.
2.张老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别探究a,b,c与n之间的关系,并用含n(n>1)的式子表示:a=________,b=________,c=________;
n2-1
2n
n2+1
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(2)猜想以a,b,c为边长的三角形是否为直角三角形,并说明你的理由.
解:是直角三角形.理由如下:因为a2+b2=(n2-1)2+(2n)2=n4+2n2+1,c2=(n2+1)2=n4+2n2+1,所以a2+b2=c2.
所以以a,b,c为边长的三角形是直角三角形.
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
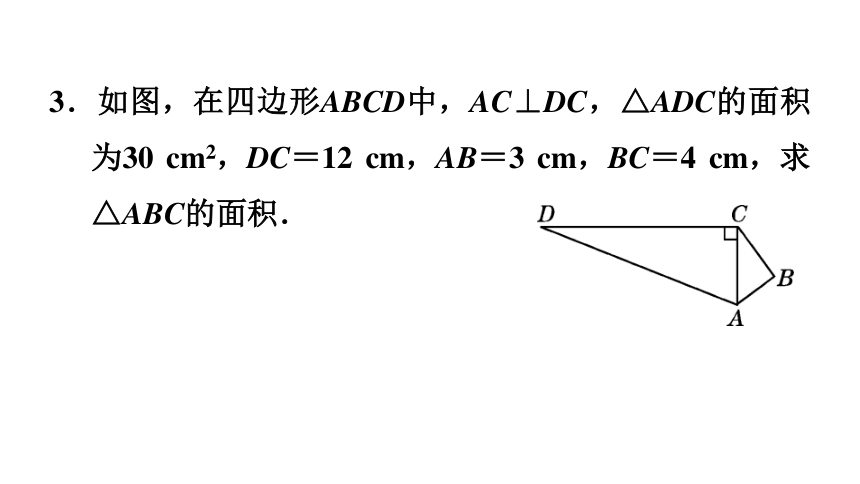
3.如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3 cm,BC=4 cm,求△ABC的面积.
4.如果x,y,z为正整数,且满足x2+y2=z2,那么(x,y,z)叫做一组勾股数.如(3,4,5)就是一组勾股数.
(1)请你再写出两组勾股数:
(________,________,________),
(________,________,________).
12 15
(答案不唯一)
6 8 10
4.如果x,y,z为正整数,且满足x2+y2=z2,那么(x,y,z)叫做一组勾股数.如(3,4,5)就是一组勾股数.
(2)在△ABC中,三条边长分别为a,b,c,其中a=n,b= -1,c= (n是大于2的偶数).试说明:(a,b,c)是一组勾 股数.
5.如图,长方体的底面相邻两边的长分别为1 cm和3 cm,高为6 cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要多长?如果从点A开始经过4个侧面缠绕n圈到达点B,那么所
用细线最短时,其长度的平方是多少?
解:将长方体的侧面展开,连接AB′,如图所示.
因为AA′=1+3+1+3=8(cm),A′B′=6 cm,
所以AB′2=AA′2+A′B′2=82+62=102.
所以用一根细线从点A开始经过4个侧面缠绕一圈到达点B,所用细线最短需要10 cm.易知如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短时,其长度的平方为(64n2+36)cm2.
6.如图,一牧童在A处牧马,牧童的家在B处,A,B处距河岸的距离分别是AC=500 m,BD=700 m,且C,D间的距离为500 m.天黑前牧童从A点将马牵到河边去饮水,再赶回家,为了使所走的路程最短.
(1)牧童应将马赶到河边的什么地点?请你在图中画出来.
解:如图,作A点关于河岸CD的对称点A′,连接BA′,交河岸于P,连接PA,则PB+PA=PB+PA′=BA′最短,故牧童应将马赶到河边的P点.
6.如图,一牧童在A处牧马,牧童的家在B处,A,B处距河岸的距离分别是AC=500 m,BD=700 m,且C,D间的距离为500 m.天黑前牧童从A点将马牵到河边去饮水,再赶回家,为了使所走的路程最短.
(2)请你求出他至少要走多少路程.
解:作A′B′⊥BD,交BD的延长线于点B′,
易知B′A′=CD,DB′=CA′=AC.
在Rt△BB′A′中,BB′=BD+DB′=BD+AC=1 200 m,A′B′=500 m,由勾股定理,得BA′=1 300 m.
所以他至少要走1 300 m.
7.如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1)猜想AP与CQ之间的数量关系,并说明你的理由.
解:猜想:AP=CQ.
理由如下:在△ABP和△CBQ中,
因为∠ABC=∠PBQ=60°,
所以∠ABP=∠ABC-∠PBC=∠PBQ-∠PBC=∠CBQ.
因为AB=CB,BP=BQ,所以△ABP≌△CBQ,所以AP=CQ.
7.如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(2)若PA∶PB∶PC=3∶4∶5,连接PQ,且△PBQ是等边三角形,试判断△PQC的形状,并说明理由.
【点拨】说明一个三角形是直角三角形的方法较多,但在已知三角形各边长度或各边长度之间的关系时,利用直角三角形的判定方法判断这个三角形是否为直角三角形,是比较常用且比较方便的方法.
解:如图,△PQC是直角三角形.理由如下:
由PA∶PB∶PC=3∶4∶5,
可设PA=3a,PB=4a,PC=5a,
因为△PBQ为等边三角形,所以PQ=PB=4a.
在△PQC中,因为CQ=AP=3a,
所以PQ2+CQ2=16a2+9a2=25a2=PC2,所以△PQC是直角三角形.
8.如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求:
(1)AC的长度;
解:因为AD是BC边上的中线,BC=10,
所以BD=CD=5.
因为52+122=132,所以BD2+AD2=AB2.
所以∠ADB=90°.所以∠ADC=90°.
所以AC2=AD2+CD2=169.所以AC=13.
8.如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求:
(2)△ABC的面积.
9.将穿好彩旗的旗杆垂直插在操场上,旗杆顶到地面的高度为320 cm,在无风的天气里,彩旗自然下垂,如图①所示.求彩旗下垂时最低处离地面的高度h(彩旗完全展开时的尺寸如图②所示).
解:彩旗下垂时最低处离地面的高度h也就是旗杆顶到地面的高度减去彩旗的对角线的长.
因为1202+902=22 500,
所以彩旗的对角线长为150 cm.
所以h=320-150=170(cm).
即彩旗下垂时最低处离地面的高度h为170 cm.
10.如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距5 n mile的A,B两个基地前去拦截,6 min后同时到达C地将其拦截.已知甲巡逻艇的速度为40 n mile/h,乙巡逻艇的速度为30 n mile/h,且乙巡逻艇的航向为北偏西37°,求甲巡逻艇的航向.
因为AB=5 n mile,所以AB2=BC2+AC2.所以∠ACB=90°.
因为∠CBA=90°-37°=53°,所以∠CAB=37°.
所以90°-∠CAB=53°.
所以甲巡逻艇的航向为北偏东53°.
11.育英中学有两个课外小组的同学同时步行到校外去采集植物标本,第一组的步行速度为30 m/min,第二组的步行速度为40 m/min,半小时后,两组同学同时停下来,这时两组同学相距1 500 m.
(1)试判断这两组同学行走的方向是否成直角;
解:因为半小时后,第一组行走的路程为30×30=900(m),
第二组行走的路程为40×30=1 200(m),9002+1 2002=1 5002,而此时两组同学相距1 500 m,所以两组同学行走的方向成直角.
11.育英中学有两个课外小组的同学同时步行到校外去采集植物标本,第一组的步行速度为30 m/min,第二组的步行速度为40 m/min,半小时后,两组同学同时停下来,这时两组同学相距1 500 m.
(2)如果接下来这两组同学以原来的速度相向而行,多长时间后能相遇?
12.如图,点N是△ABC的边BC的延长线上一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.
(1)若∠APC=30°,试说明:AB=AP.
解:过点A作AE⊥BP于点E.
因为AC⊥AP,所以∠CAP=90°.
因为∠APC=30°,所以∠ACP=60°.
因为∠ACN=2∠BAC,所以∠BAC=30°.所以易得∠ABP=30°.
所以∠ABP=∠APC.因为AE⊥BP,所以∠AEB=∠AEP=90°.
又因为AE=AE,所以△AEB≌△AEP. 所以AB=AP.
12.如图,点N是△ABC的边BC的延长线上一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.
(2)若AP=8,BP=16,求AC的长.
解:因为∠ACP=180°-∠ACB,∠BAC+∠B+∠ACB=180°,
所以∠ACP=∠BAC+∠B.
又因为∠ACN=2∠BAC,所以∠BAC=∠B,易得AC=BC.
设AC=x,则BC=x.在Rt△ACP中,由勾股定理建立方程得
x2+82=(16-x)2,解得x=6. 所以AC=6.
12.如图,点N是△ABC的边BC的延长线上一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.
(3)若点P在BC的延长线上运动,∠APB的平分线交AB于点M.你认为∠AMP的大小是否发生变化?若变化,请说明理由;若不变化,求出∠AMP的大小.
解:∠AMP的大小不发生变化.
13.求下列图形中阴影部分的面积.
(1)如图①,BA⊥CA,AB=8,AC=6;
解:因为AB=8,AC=6,BA⊥AC,
所以BC2=AB2+AC2=100.所以BC=10.所以BO=5.
13.求下列图形中阴影部分的面积.
(2)如图②,四边形BCDE为长方形,
AB=13,AD=14,CD=2.
解:因为AD=14,CD=2,所以AC=12.
因为AB=13,∠ACB=90°,
所以CB2=AB2-AC2=25.所以CB=5.
所以S阴影=2×5=10.
14.如图,在△ABC中,∠C=90°,AB=10 cm,BC=6 cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为1 cm/s,设运动时间为t s.
(1)出发2 s后,求△ABP的面积.
解:如图,因为∠C=90°,AB=10 cm,
BC=6 cm,所以AC=8 cm.
14.如图,在△ABC中,∠C=90°,AB=10 cm,BC=6 cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为1 cm/s,设运动时间为t s.
(2)当t为何值时,BP平分∠ABC?
解:如图,过点P作PD⊥AB于点D,
当BP平分∠ABC时,有PD=PC,
易得△BPD≌△BPC,
所以BD=BC=6 cm.
所以AD=10-6=4(cm).
14.如图,在△ABC中,∠C=90°,AB=10 cm,BC=6 cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为1 cm/s,设运动时间为t s.
(3)当t为何值时,△BCP为等腰三角形?
如图①,若点P在边AC上,BC=CP=6 cm,
所以点P运动的路程为6 cm.
故当t=6时,△BCP为等腰三角形.
若点P在AB边上时,有三种情况:
如图②,若BP=CB=6 cm,此时AP=4 cm,
所以点P运动的路程为12 cm.
故当t=12时,△BCP为等腰三角形;
如图③,若CP=BC=6 cm,
过C作CE⊥AB于点E,
根据面积法求得CE=4.8 cm,
根据勾股定理得PE=BE=3.6 cm.
所以BP=7.2 cm,
所以点P运动的路程为18-7.2=10.8(cm).
所以当t=10.8时,△BCP为等腰三角形.
如图④,若BP=CP,则∠PCB=∠PBC,
因为∠ACP+∠BCP=90°,∠PBC+∠CAP=90°,
所以∠ACP=∠CAP.易得PA=PC.
所以PA=PB=5 cm.
所以点P运动的路程为13 cm.
所以当t=13时,△BCP为等腰三角形.
所以当t=6或10.8或12或13时,△BCP为等腰三角形.
全章热门考点整合应用
第一章 勾股定理
答案显示
(64n2+36)cm2
1 300 m.
(1)AP=CQ.
(2)△PQC是直角三角形.
12
(1)n2-1;2n;n2+1
(2)直角三角形.
6cm2
(1)6;8;10;9;12;15(答案不唯一)
(2)是一组勾股数.
答案显示
170 cm
(1)AC=13. (2)60.
北偏东53°
(1)18cm2 (2)t=3
(3)t=6或10.8或12或13时
(1)AB=AP. (2)AC=6.
(3)∠AMP的大小不发生变化.
1.如图,在△ABC中,∠ACB=90°,BC=15,AC=20,CD是高.求:
(1)AB的长;
解:因为在△ABC中,∠ACB=90°,BC=15,AC=20,
所以AB2=AC2+BC2=202+152=625.
所以AB=25.
1.如图,在△ABC中,∠ACB=90°,
BC=15,AC=20,CD是高.求:
(2)△ABC的面积;
(3)CD的长.
2.张老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别探究a,b,c与n之间的关系,并用含n(n>1)的式子表示:a=________,b=________,c=________;
n2-1
2n
n2+1
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(2)猜想以a,b,c为边长的三角形是否为直角三角形,并说明你的理由.
解:是直角三角形.理由如下:因为a2+b2=(n2-1)2+(2n)2=n4+2n2+1,c2=(n2+1)2=n4+2n2+1,所以a2+b2=c2.
所以以a,b,c为边长的三角形是直角三角形.
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
3.如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3 cm,BC=4 cm,求△ABC的面积.
4.如果x,y,z为正整数,且满足x2+y2=z2,那么(x,y,z)叫做一组勾股数.如(3,4,5)就是一组勾股数.
(1)请你再写出两组勾股数:
(________,________,________),
(________,________,________).
12 15
(答案不唯一)
6 8 10
4.如果x,y,z为正整数,且满足x2+y2=z2,那么(x,y,z)叫做一组勾股数.如(3,4,5)就是一组勾股数.
(2)在△ABC中,三条边长分别为a,b,c,其中a=n,b= -1,c= (n是大于2的偶数).试说明:(a,b,c)是一组勾 股数.
5.如图,长方体的底面相邻两边的长分别为1 cm和3 cm,高为6 cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要多长?如果从点A开始经过4个侧面缠绕n圈到达点B,那么所
用细线最短时,其长度的平方是多少?
解:将长方体的侧面展开,连接AB′,如图所示.
因为AA′=1+3+1+3=8(cm),A′B′=6 cm,
所以AB′2=AA′2+A′B′2=82+62=102.
所以用一根细线从点A开始经过4个侧面缠绕一圈到达点B,所用细线最短需要10 cm.易知如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短时,其长度的平方为(64n2+36)cm2.
6.如图,一牧童在A处牧马,牧童的家在B处,A,B处距河岸的距离分别是AC=500 m,BD=700 m,且C,D间的距离为500 m.天黑前牧童从A点将马牵到河边去饮水,再赶回家,为了使所走的路程最短.
(1)牧童应将马赶到河边的什么地点?请你在图中画出来.
解:如图,作A点关于河岸CD的对称点A′,连接BA′,交河岸于P,连接PA,则PB+PA=PB+PA′=BA′最短,故牧童应将马赶到河边的P点.
6.如图,一牧童在A处牧马,牧童的家在B处,A,B处距河岸的距离分别是AC=500 m,BD=700 m,且C,D间的距离为500 m.天黑前牧童从A点将马牵到河边去饮水,再赶回家,为了使所走的路程最短.
(2)请你求出他至少要走多少路程.
解:作A′B′⊥BD,交BD的延长线于点B′,
易知B′A′=CD,DB′=CA′=AC.
在Rt△BB′A′中,BB′=BD+DB′=BD+AC=1 200 m,A′B′=500 m,由勾股定理,得BA′=1 300 m.
所以他至少要走1 300 m.
7.如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1)猜想AP与CQ之间的数量关系,并说明你的理由.
解:猜想:AP=CQ.
理由如下:在△ABP和△CBQ中,
因为∠ABC=∠PBQ=60°,
所以∠ABP=∠ABC-∠PBC=∠PBQ-∠PBC=∠CBQ.
因为AB=CB,BP=BQ,所以△ABP≌△CBQ,所以AP=CQ.
7.如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(2)若PA∶PB∶PC=3∶4∶5,连接PQ,且△PBQ是等边三角形,试判断△PQC的形状,并说明理由.
【点拨】说明一个三角形是直角三角形的方法较多,但在已知三角形各边长度或各边长度之间的关系时,利用直角三角形的判定方法判断这个三角形是否为直角三角形,是比较常用且比较方便的方法.
解:如图,△PQC是直角三角形.理由如下:
由PA∶PB∶PC=3∶4∶5,
可设PA=3a,PB=4a,PC=5a,
因为△PBQ为等边三角形,所以PQ=PB=4a.
在△PQC中,因为CQ=AP=3a,
所以PQ2+CQ2=16a2+9a2=25a2=PC2,所以△PQC是直角三角形.
8.如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求:
(1)AC的长度;
解:因为AD是BC边上的中线,BC=10,
所以BD=CD=5.
因为52+122=132,所以BD2+AD2=AB2.
所以∠ADB=90°.所以∠ADC=90°.
所以AC2=AD2+CD2=169.所以AC=13.
8.如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求:
(2)△ABC的面积.
9.将穿好彩旗的旗杆垂直插在操场上,旗杆顶到地面的高度为320 cm,在无风的天气里,彩旗自然下垂,如图①所示.求彩旗下垂时最低处离地面的高度h(彩旗完全展开时的尺寸如图②所示).
解:彩旗下垂时最低处离地面的高度h也就是旗杆顶到地面的高度减去彩旗的对角线的长.
因为1202+902=22 500,
所以彩旗的对角线长为150 cm.
所以h=320-150=170(cm).
即彩旗下垂时最低处离地面的高度h为170 cm.
10.如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距5 n mile的A,B两个基地前去拦截,6 min后同时到达C地将其拦截.已知甲巡逻艇的速度为40 n mile/h,乙巡逻艇的速度为30 n mile/h,且乙巡逻艇的航向为北偏西37°,求甲巡逻艇的航向.
因为AB=5 n mile,所以AB2=BC2+AC2.所以∠ACB=90°.
因为∠CBA=90°-37°=53°,所以∠CAB=37°.
所以90°-∠CAB=53°.
所以甲巡逻艇的航向为北偏东53°.
11.育英中学有两个课外小组的同学同时步行到校外去采集植物标本,第一组的步行速度为30 m/min,第二组的步行速度为40 m/min,半小时后,两组同学同时停下来,这时两组同学相距1 500 m.
(1)试判断这两组同学行走的方向是否成直角;
解:因为半小时后,第一组行走的路程为30×30=900(m),
第二组行走的路程为40×30=1 200(m),9002+1 2002=1 5002,而此时两组同学相距1 500 m,所以两组同学行走的方向成直角.
11.育英中学有两个课外小组的同学同时步行到校外去采集植物标本,第一组的步行速度为30 m/min,第二组的步行速度为40 m/min,半小时后,两组同学同时停下来,这时两组同学相距1 500 m.
(2)如果接下来这两组同学以原来的速度相向而行,多长时间后能相遇?
12.如图,点N是△ABC的边BC的延长线上一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.
(1)若∠APC=30°,试说明:AB=AP.
解:过点A作AE⊥BP于点E.
因为AC⊥AP,所以∠CAP=90°.
因为∠APC=30°,所以∠ACP=60°.
因为∠ACN=2∠BAC,所以∠BAC=30°.所以易得∠ABP=30°.
所以∠ABP=∠APC.因为AE⊥BP,所以∠AEB=∠AEP=90°.
又因为AE=AE,所以△AEB≌△AEP. 所以AB=AP.
12.如图,点N是△ABC的边BC的延长线上一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.
(2)若AP=8,BP=16,求AC的长.
解:因为∠ACP=180°-∠ACB,∠BAC+∠B+∠ACB=180°,
所以∠ACP=∠BAC+∠B.
又因为∠ACN=2∠BAC,所以∠BAC=∠B,易得AC=BC.
设AC=x,则BC=x.在Rt△ACP中,由勾股定理建立方程得
x2+82=(16-x)2,解得x=6. 所以AC=6.
12.如图,点N是△ABC的边BC的延长线上一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.
(3)若点P在BC的延长线上运动,∠APB的平分线交AB于点M.你认为∠AMP的大小是否发生变化?若变化,请说明理由;若不变化,求出∠AMP的大小.
解:∠AMP的大小不发生变化.
13.求下列图形中阴影部分的面积.
(1)如图①,BA⊥CA,AB=8,AC=6;
解:因为AB=8,AC=6,BA⊥AC,
所以BC2=AB2+AC2=100.所以BC=10.所以BO=5.
13.求下列图形中阴影部分的面积.
(2)如图②,四边形BCDE为长方形,
AB=13,AD=14,CD=2.
解:因为AD=14,CD=2,所以AC=12.
因为AB=13,∠ACB=90°,
所以CB2=AB2-AC2=25.所以CB=5.
所以S阴影=2×5=10.
14.如图,在△ABC中,∠C=90°,AB=10 cm,BC=6 cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为1 cm/s,设运动时间为t s.
(1)出发2 s后,求△ABP的面积.
解:如图,因为∠C=90°,AB=10 cm,
BC=6 cm,所以AC=8 cm.
14.如图,在△ABC中,∠C=90°,AB=10 cm,BC=6 cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为1 cm/s,设运动时间为t s.
(2)当t为何值时,BP平分∠ABC?
解:如图,过点P作PD⊥AB于点D,
当BP平分∠ABC时,有PD=PC,
易得△BPD≌△BPC,
所以BD=BC=6 cm.
所以AD=10-6=4(cm).
14.如图,在△ABC中,∠C=90°,AB=10 cm,BC=6 cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为1 cm/s,设运动时间为t s.
(3)当t为何值时,△BCP为等腰三角形?
如图①,若点P在边AC上,BC=CP=6 cm,
所以点P运动的路程为6 cm.
故当t=6时,△BCP为等腰三角形.
若点P在AB边上时,有三种情况:
如图②,若BP=CB=6 cm,此时AP=4 cm,
所以点P运动的路程为12 cm.
故当t=12时,△BCP为等腰三角形;
如图③,若CP=BC=6 cm,
过C作CE⊥AB于点E,
根据面积法求得CE=4.8 cm,
根据勾股定理得PE=BE=3.6 cm.
所以BP=7.2 cm,
所以点P运动的路程为18-7.2=10.8(cm).
所以当t=10.8时,△BCP为等腰三角形.
如图④,若BP=CP,则∠PCB=∠PBC,
因为∠ACP+∠BCP=90°,∠PBC+∠CAP=90°,
所以∠ACP=∠CAP.易得PA=PC.
所以PA=PB=5 cm.
所以点P运动的路程为13 cm.
所以当t=13时,△BCP为等腰三角形.
所以当t=6或10.8或12或13时,△BCP为等腰三角形.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
