北师大版八上数学第1章勾股定理:全章热门考点整合专训课件(34张PPT)
文档属性
| 名称 | 北师大版八上数学第1章勾股定理:全章热门考点整合专训课件(34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 715.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 14:02:19 | ||
图片预览











文档简介
(共34张PPT)
全章热门考点整合专训
第一章 勾股定理
答案显示
图略 150万元
135°
1.4
(1)n2-1;2n;n2+1
(2)是直角三角形.
C
10 cm.
(64n2+36)cm2
答案显示
过点C作公路AB的垂线,垂足为D,则线段CD即为新建的路. 480 m
答案显示
60或42
1.如图,在Rt△ABC中,∠C=90°,点D是BC上一点,AD=BD.若AB=8,BD=5,求CD的长.
解:设CD=x.
在Rt△ABC中,有AC2+(CD+BD)2=AB2,
整理,得AC2=AB2-(CD+BD)2=64-(x+5)2.①
在Rt△ADC中,有AC2+CD2=AD2,
整理,得AC2=AD2-CD2=25-x2.②
由①②两式,得64-(x+5)2=25-x2,解得x=1.4.
即CD的长是1.4.
2.张老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别探究a,b,c与n之间的关系,并且用含n(n>1且n为整数)的式子表示:
a=________,b=________,c=________;
n2-1
2n
n2+1
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(2)猜想以a,b,c为边长的三角形是否为直角三角形,并说明理由.
解:是直角三角形.理由如下:
因为a2+b2=(n2-1)2+(2n)2=n4+2n2+1,
c2=(n2+1)2=n4+2n2+1,
所以a2+b2=c2.
所以以a,b,c为边长的三角形是直角三角形.
C
4.如图,长方体的底面相邻两边的长分别为1 cm和3 cm,高为6 cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要多长?如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短时其长度的平方是多少?
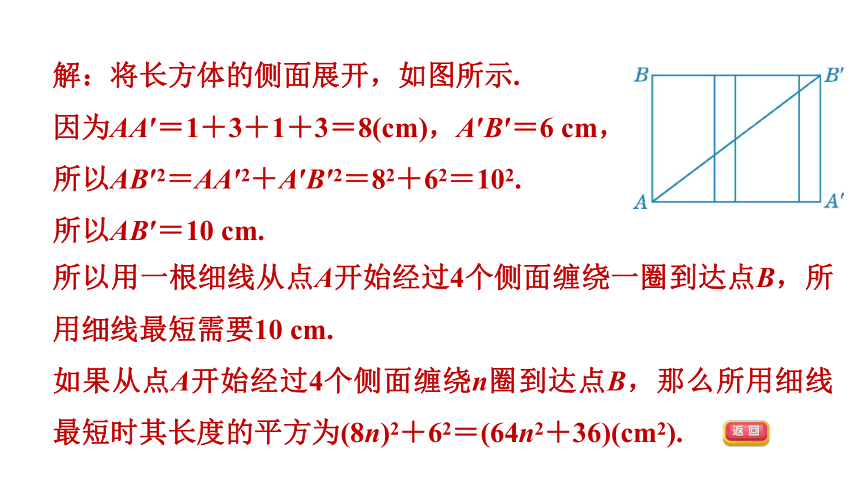
解:将长方体的侧面展开,如图所示.
因为AA′=1+3+1+3=8(cm),A′B′=6 cm,
所以AB′2=AA′2+A′B′2=82+62=102.
所以AB′=10 cm.
所以用一根细线从点A开始经过4个侧面缠绕一圈到达点B,所用细线最短需要10 cm.
如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短时其长度的平方为(8n)2+62=(64n2+36)(cm2).
5.如图,A,B两个小镇在河岸l的同侧,到河岸的距离分别为AC=10 km,BD=30 km,且CD=30 km,现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万元.请你在河岸l上选择自来水厂的位置M,使铺设水管的费用最节省,
并求出最少的费用是多少.
解:如图,作点A关于直线l的对称点A′,
连接A′B,交CD于点M,点M即为所求.
连接AM,则MA+MB最小.作A′E⊥BD,
且交BD的延长线于点E.
在Rt△A′BE中,A′E=30 km,BE=BD+DE=BD+AC=40 km.
由勾股定理得A′B2=A′E2+BE2=302+402=502,所以A′B=50 km.
所以MA+MB=A′M+BM=A′B=50 km.
所以铺设水管的最少费用为50×3=150(万元).
6.如图,点E是正方形ABCD内一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,求∠BE′C的度数.
解:如图,连接EE′.
由题意可知△ABE≌△CBE′,∠EBE′=90°,
所以E′C=AE=1,BE′=BE=2,
∠ABE=∠CBE′.
7.如图,已知等腰三角形ABC的底边长BC=20 cm,D是AC上的一点,且BD=16 cm,CD=12 cm.
(1)试说明:BD⊥AC;
解:因为122+162=202,
所以CD2+BD2=BC2.
所以△BDC是直角三角形,且∠BDC=90°.
所以BD⊥AC.
7.如图,已知等腰三角形ABC的底边长BC=20 cm,D是AC上的一点,且BD=16 cm,CD=12 cm.
(2)求△ABC的面积.
解:设AD=x cm,则AC=(x+12)cm.
因为AB=AC,所以AB=(x+12)cm.
8.如图,有一块直角三角形绿地,量得两直角边BC,AC的长分别为6 m,8 m.现要将绿地扩充成等腰三角形,且扩充部分是以AC边为直角边的直角三角形,求扩充后的等腰三角形绿地的面积.
解:在Rt△ABC中,∠ACB=90°,AC=8 m,BC=6 m,由勾股定理得AB2=AC2+BC2=82+62=100,
所以AB=10 m.
设扩充部分为Rt△ACD,扩充成等腰三角形ABD,应分以下三种情况讨论:
9.如图,某工厂C前面有一条笔直的公路,原来有两条路AC,BC可以从工厂C到达公路,经测量AC=600 m,BC=800 m,AB=1 000 m,现需要修建一条路,使工厂C到公路的距离最短.请你帮工厂C的负责人设计一种方案,并求出新建的路的长.
解:过点C作公路AB的垂线,垂足为D,则线段CD即为新建的路.
因为AC2+BC2=6002+8002=1 0002,AB2=1 0002,
所以AC2+BC2=AB2.
所以△ABC为直角三角形,且∠ACB=90°.
10.育英中学有两个课外小组的同学同时步行到校外去采集植物标本,第一组的步行速度为30 m/min,第二组的步行速度为40 m/min,30 min后,两组同学同时停下来,这时两组同学相距1 500 m.
(1)试判断这两组同学行走的方向是否成直角;
解:30 min后,第一组行走的路程为30×30=900(m),第二组行走的路程为40×30=1 200(m).
因为9002+1 2002=1 5002,且此时两组同学相距1 500 m,
所以两组同学行走的方向成直角.
10.育英中学有两个课外小组的同学同时步行到校外去采集植物标本,第一组的步行速度为30 m/min,第二组的步行速度为40 m/min,30 min后,两组同学同时停下来,这时两组同学相距1 500 m.
(2)如果接下来这两组同学以原来的速度相向而行,多长时间后能相遇?
11.如图,将长方形ABCD的边AD沿折痕AE折叠,使点D落在BC边上的点F处.已知AB=6,△ABF的面积是24,求EF的长.
12.阅读下列材料:
如图①,一圆柱的底面半径为5,高AB为5,BC是底面直径,一只蚂蚁从A点出发沿圆柱表面爬到点C,为探索蚂蚁爬行的最短路线,小明设计了两条路线.
路线1:侧面展开图中的线段AC,如图②所示.
设路线1的长度为l1,
则l12=AC2=AB2+BC2=52+(5π)2=25+25π2.
路线2:高线AB+底面直径BC.
设路线2的长度为l2,则l22=(AB+BC)2=(5+10)2=225.
因为l12-l22=25+25π2-225=25π2-200=25(π2-8)>0,
所以l12>l22.所以l1>l2,即路线2较短.
【点拨】勾股定理是从形到数的转化,直角三角形的判定是从数到形的转化.本章题目中还有把四边形问题转化为三角形的问题,把立体图形问题转化为平面图形的问题,这些都体现了数学中的转化思想.
(1)小明对上述结论有些疑惑,于是他把条件改成:圆柱的底面半径为1,高AB为5,继续按前面的路线进行计算.请你帮小明完成下面的计算.
路线1:l12=AC2=________;
路线2:l22=(AB+BC)2=________.
因为l12______l22,
所以l1______l2(填“>”或“<”).
所以路线______(填“1”或“2”)较短.
1
25+π2
49
<
<
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线,才能使蚂蚁从点A出发沿圆柱表面爬到点C的路线较短?
解:
设路线1的长度为l1,则l12=AC2=AB2+BC2=h2+(πr)2=h2+π2r2.
设路线2的长度为l2,则l22=(AB+BC)2=(h+2r)2=h2+4rh+4r2.
13.在△ABC中,若AB=20,AC=15,BC边上的高为12,求△ABC的周长.
解:设BC边上的高为AD,则△ABD,△ACD是直角三角形,
由勾股定理得BD2=AB2-AD2=202-122=256,
CD2=AC2-AD2=152-122=81,
所以BD=16,CD=9.
①若∠ACB是锐角,如图①,则BC=BD+CD=16+9=25.
所以△ABC的周长为AB+AC+BC=20+15+25=60.
②若∠ACB是钝角,如图②,则BC=BD-CD=16-9=7.
所以△ABC的周长为AB+AC+BC=20+15+7=42.
综上所述,△ABC的周长为60或42.
全章热门考点整合专训
第一章 勾股定理
答案显示
图略 150万元
135°
1.4
(1)n2-1;2n;n2+1
(2)是直角三角形.
C
10 cm.
(64n2+36)cm2
答案显示
过点C作公路AB的垂线,垂足为D,则线段CD即为新建的路. 480 m
答案显示
60或42
1.如图,在Rt△ABC中,∠C=90°,点D是BC上一点,AD=BD.若AB=8,BD=5,求CD的长.
解:设CD=x.
在Rt△ABC中,有AC2+(CD+BD)2=AB2,
整理,得AC2=AB2-(CD+BD)2=64-(x+5)2.①
在Rt△ADC中,有AC2+CD2=AD2,
整理,得AC2=AD2-CD2=25-x2.②
由①②两式,得64-(x+5)2=25-x2,解得x=1.4.
即CD的长是1.4.
2.张老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别探究a,b,c与n之间的关系,并且用含n(n>1且n为整数)的式子表示:
a=________,b=________,c=________;
n2-1
2n
n2+1
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(2)猜想以a,b,c为边长的三角形是否为直角三角形,并说明理由.
解:是直角三角形.理由如下:
因为a2+b2=(n2-1)2+(2n)2=n4+2n2+1,
c2=(n2+1)2=n4+2n2+1,
所以a2+b2=c2.
所以以a,b,c为边长的三角形是直角三角形.
C
4.如图,长方体的底面相邻两边的长分别为1 cm和3 cm,高为6 cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要多长?如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短时其长度的平方是多少?
解:将长方体的侧面展开,如图所示.
因为AA′=1+3+1+3=8(cm),A′B′=6 cm,
所以AB′2=AA′2+A′B′2=82+62=102.
所以AB′=10 cm.
所以用一根细线从点A开始经过4个侧面缠绕一圈到达点B,所用细线最短需要10 cm.
如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短时其长度的平方为(8n)2+62=(64n2+36)(cm2).
5.如图,A,B两个小镇在河岸l的同侧,到河岸的距离分别为AC=10 km,BD=30 km,且CD=30 km,现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万元.请你在河岸l上选择自来水厂的位置M,使铺设水管的费用最节省,
并求出最少的费用是多少.
解:如图,作点A关于直线l的对称点A′,
连接A′B,交CD于点M,点M即为所求.
连接AM,则MA+MB最小.作A′E⊥BD,
且交BD的延长线于点E.
在Rt△A′BE中,A′E=30 km,BE=BD+DE=BD+AC=40 km.
由勾股定理得A′B2=A′E2+BE2=302+402=502,所以A′B=50 km.
所以MA+MB=A′M+BM=A′B=50 km.
所以铺设水管的最少费用为50×3=150(万元).
6.如图,点E是正方形ABCD内一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,求∠BE′C的度数.
解:如图,连接EE′.
由题意可知△ABE≌△CBE′,∠EBE′=90°,
所以E′C=AE=1,BE′=BE=2,
∠ABE=∠CBE′.
7.如图,已知等腰三角形ABC的底边长BC=20 cm,D是AC上的一点,且BD=16 cm,CD=12 cm.
(1)试说明:BD⊥AC;
解:因为122+162=202,
所以CD2+BD2=BC2.
所以△BDC是直角三角形,且∠BDC=90°.
所以BD⊥AC.
7.如图,已知等腰三角形ABC的底边长BC=20 cm,D是AC上的一点,且BD=16 cm,CD=12 cm.
(2)求△ABC的面积.
解:设AD=x cm,则AC=(x+12)cm.
因为AB=AC,所以AB=(x+12)cm.
8.如图,有一块直角三角形绿地,量得两直角边BC,AC的长分别为6 m,8 m.现要将绿地扩充成等腰三角形,且扩充部分是以AC边为直角边的直角三角形,求扩充后的等腰三角形绿地的面积.
解:在Rt△ABC中,∠ACB=90°,AC=8 m,BC=6 m,由勾股定理得AB2=AC2+BC2=82+62=100,
所以AB=10 m.
设扩充部分为Rt△ACD,扩充成等腰三角形ABD,应分以下三种情况讨论:
9.如图,某工厂C前面有一条笔直的公路,原来有两条路AC,BC可以从工厂C到达公路,经测量AC=600 m,BC=800 m,AB=1 000 m,现需要修建一条路,使工厂C到公路的距离最短.请你帮工厂C的负责人设计一种方案,并求出新建的路的长.
解:过点C作公路AB的垂线,垂足为D,则线段CD即为新建的路.
因为AC2+BC2=6002+8002=1 0002,AB2=1 0002,
所以AC2+BC2=AB2.
所以△ABC为直角三角形,且∠ACB=90°.
10.育英中学有两个课外小组的同学同时步行到校外去采集植物标本,第一组的步行速度为30 m/min,第二组的步行速度为40 m/min,30 min后,两组同学同时停下来,这时两组同学相距1 500 m.
(1)试判断这两组同学行走的方向是否成直角;
解:30 min后,第一组行走的路程为30×30=900(m),第二组行走的路程为40×30=1 200(m).
因为9002+1 2002=1 5002,且此时两组同学相距1 500 m,
所以两组同学行走的方向成直角.
10.育英中学有两个课外小组的同学同时步行到校外去采集植物标本,第一组的步行速度为30 m/min,第二组的步行速度为40 m/min,30 min后,两组同学同时停下来,这时两组同学相距1 500 m.
(2)如果接下来这两组同学以原来的速度相向而行,多长时间后能相遇?
11.如图,将长方形ABCD的边AD沿折痕AE折叠,使点D落在BC边上的点F处.已知AB=6,△ABF的面积是24,求EF的长.
12.阅读下列材料:
如图①,一圆柱的底面半径为5,高AB为5,BC是底面直径,一只蚂蚁从A点出发沿圆柱表面爬到点C,为探索蚂蚁爬行的最短路线,小明设计了两条路线.
路线1:侧面展开图中的线段AC,如图②所示.
设路线1的长度为l1,
则l12=AC2=AB2+BC2=52+(5π)2=25+25π2.
路线2:高线AB+底面直径BC.
设路线2的长度为l2,则l22=(AB+BC)2=(5+10)2=225.
因为l12-l22=25+25π2-225=25π2-200=25(π2-8)>0,
所以l12>l22.所以l1>l2,即路线2较短.
【点拨】勾股定理是从形到数的转化,直角三角形的判定是从数到形的转化.本章题目中还有把四边形问题转化为三角形的问题,把立体图形问题转化为平面图形的问题,这些都体现了数学中的转化思想.
(1)小明对上述结论有些疑惑,于是他把条件改成:圆柱的底面半径为1,高AB为5,继续按前面的路线进行计算.请你帮小明完成下面的计算.
路线1:l12=AC2=________;
路线2:l22=(AB+BC)2=________.
因为l12______l22,
所以l1______l2(填“>”或“<”).
所以路线______(填“1”或“2”)较短.
1
25+π2
49
<
<
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线,才能使蚂蚁从点A出发沿圆柱表面爬到点C的路线较短?
解:
设路线1的长度为l1,则l12=AC2=AB2+BC2=h2+(πr)2=h2+π2r2.
设路线2的长度为l2,则l22=(AB+BC)2=(h+2r)2=h2+4rh+4r2.
13.在△ABC中,若AB=20,AC=15,BC边上的高为12,求△ABC的周长.
解:设BC边上的高为AD,则△ABD,△ACD是直角三角形,
由勾股定理得BD2=AB2-AD2=202-122=256,
CD2=AC2-AD2=152-122=81,
所以BD=16,CD=9.
①若∠ACB是锐角,如图①,则BC=BD+CD=16+9=25.
所以△ABC的周长为AB+AC+BC=20+15+25=60.
②若∠ACB是钝角,如图②,则BC=BD-CD=16-9=7.
所以△ABC的周长为AB+AC+BC=20+15+7=42.
综上所述,△ABC的周长为60或42.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
