人教版七年级数学下册课件:8.2加减消元法解二元一次方程组(共23张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:8.2加减消元法解二元一次方程组(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 241.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 17:16:43 | ||
图片预览






文档简介
(共23张PPT)
消元——解二元一次方程组
加减消元法
1.解二元一次方程组
2.解二元一次方程组
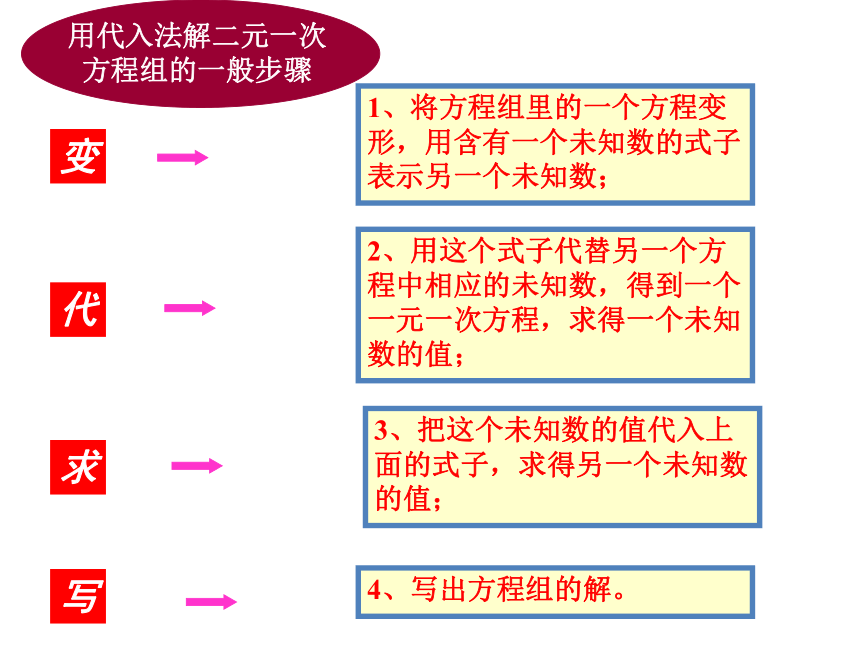
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
王阿姨在水果批发市场买了2千克苹果和4千克梨共花了14元,李阿姨以同样的价格买了2千克苹果和3千克梨共花了12元,求:苹果和梨每千克的售价各是多少元?
解方程组
从上面两个方程组的解法可以看出:当二元一次方程组的两个方程中同一未知数的系数互为相反数或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程.这种方法叫做加减消元法,简称加减法.
方法总结:
例:用加减法解方程组
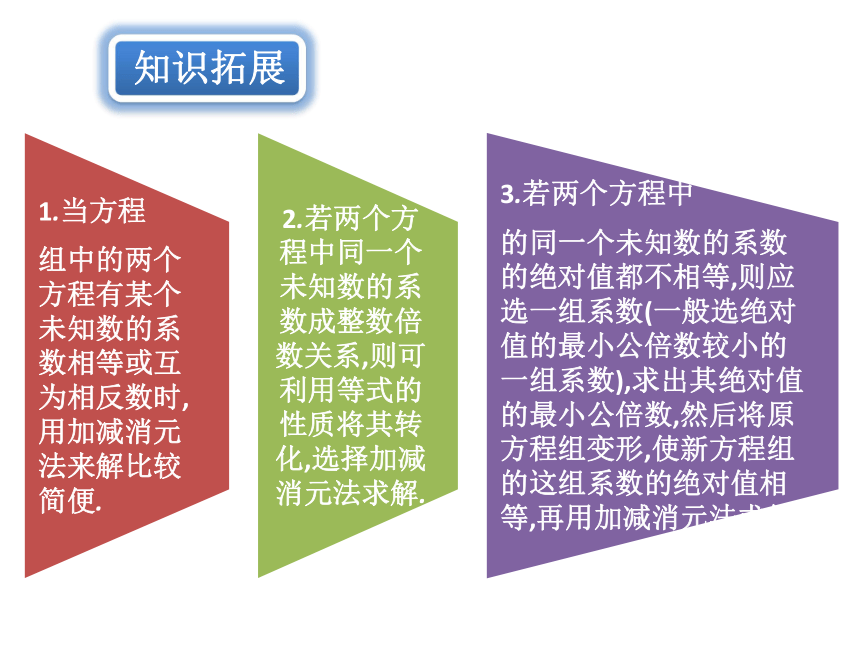
知识拓展
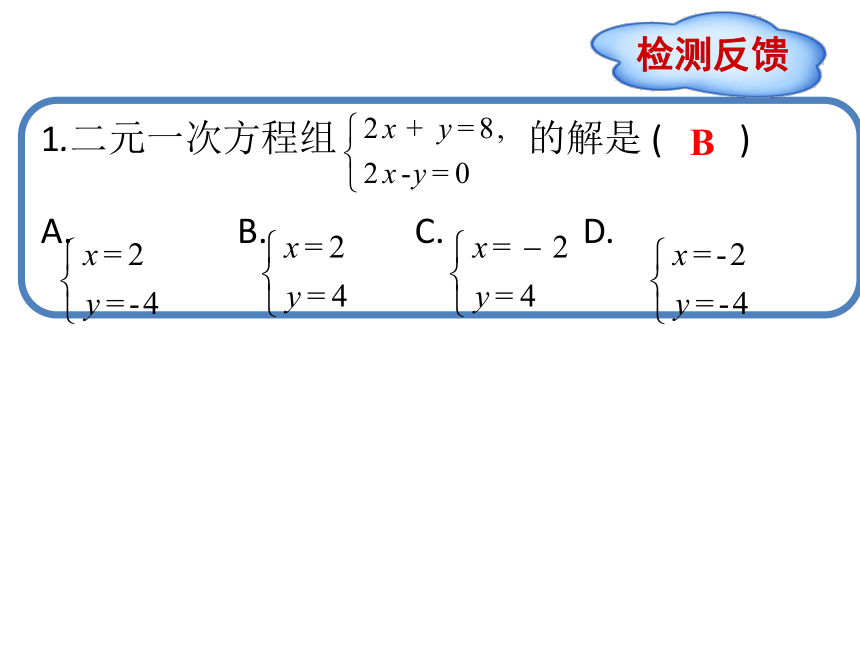
1.二元一次方程组 的解是 ( )
A. B. C. D.
检测反馈
B
2.若方程mx+ny=6的两个解是
和 则m,n的值为 ( )
A.4,2 B.2,4 C.- 4,- 2 D.- 2,- 4
解析:将 分别代入mx+ny=6中,得
①+②得:3m=12,即m=4,将m=4代入①得:n=2.故选A.
A
3.解方程组:
儿童节期间,文具商店搞促销活动,同时购买一个书包和一个文具盒可以打5折优惠,能比标价省13.2元.已知书包标价比文具盒标价的2倍少6元,那么书包和文具盒的标价各是多少元?
想一想
学 习 新 知
例:2台大收割机和5台小收割机同时工作2 h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
解:设1台大收割机和1台小收割机每小时各收割小麦x hm2和y hm2. 根据两种工作方式中的相等关系,
得方程组
去括号,得
②- ①,得11x=4.4.
解这个方程,得x=0.4.
把x=0.4代入①,得y=0.2.
因此,这个方程组的解是
答:1台大收割机和1台小收割机每小时各收割小麦0.4 hm2和0.2 hm2.
知识拓展
1.对于比较复杂的二元一次方程组,应先化简(去分母、去括号、移项、合并同类项等),通常要把每个方程整理成含有未知数的项在方程的左边,常数项在方程的右边的形式.
2.当方程组比较复杂时,应通过去分母、去括号、移项、合并同类项等,使之化为 的形式(同类项对齐),为加减消元创造有利条件.
知识拓展
3.用加减法解二元一次方程组适合于同一未知数的系数成整数倍数的情形,如果不成整数倍,那么可以将两个方程都乘一个适当的数,便于加减,另外,如果系数是分数的形式,那么要整理成 的形式,再选择适当的方法求解.
课堂小结
课堂小结
解二元一次方程组:
(1)
(6)
(5)
(3)
(4)
(2)
1.已知方程组 的解为 则2a- 3b的值为 ( )
A.4 B.6 C.- 6 D.- 4
解析: 把代入原方程组,得 用加减消元
法解得 2a- 3b=2× - 3×(- 1)=6.故选B.
检测反馈
B
2.解以下两个方程组,较为简便的是( )
A.(1)(2)均用代入法 B.(1)(2)均用加减法
C.(1)用代入法,(2)用加减法 D.(1)用加减法,(2)用代入法
解析: (1)中的第一个方程是用x表示y的形式,用代入法解答合适;(2)中的未知数t的系数互为相反数,用加减法比较合适.故选C.
C
解:原方程组可化为
①×2+②得11x=22,∴x=2,
把x=2代入①得y=3.
∴方程组的解为
解方程组
4.王大伯承包了25亩土地,今年春季改种茄子和西红柿两种大棚蔬菜,总支出44000元.其中种茄子每亩支出1700元,每亩获纯利2400元;种西红柿每亩支出1800元,每亩获纯利2600元.王大伯一共获纯利多少元?
解:设王大伯种了x亩茄子,y亩西红柿,根据题意,得
解得
一共获纯利:2400×10+2600×15=63000(元).
答:王大伯一共获纯利63000元.
消元——解二元一次方程组
加减消元法
1.解二元一次方程组
2.解二元一次方程组
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
王阿姨在水果批发市场买了2千克苹果和4千克梨共花了14元,李阿姨以同样的价格买了2千克苹果和3千克梨共花了12元,求:苹果和梨每千克的售价各是多少元?
解方程组
从上面两个方程组的解法可以看出:当二元一次方程组的两个方程中同一未知数的系数互为相反数或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程.这种方法叫做加减消元法,简称加减法.
方法总结:
例:用加减法解方程组
知识拓展
1.二元一次方程组 的解是 ( )
A. B. C. D.
检测反馈
B
2.若方程mx+ny=6的两个解是
和 则m,n的值为 ( )
A.4,2 B.2,4 C.- 4,- 2 D.- 2,- 4
解析:将 分别代入mx+ny=6中,得
①+②得:3m=12,即m=4,将m=4代入①得:n=2.故选A.
A
3.解方程组:
儿童节期间,文具商店搞促销活动,同时购买一个书包和一个文具盒可以打5折优惠,能比标价省13.2元.已知书包标价比文具盒标价的2倍少6元,那么书包和文具盒的标价各是多少元?
想一想
学 习 新 知
例:2台大收割机和5台小收割机同时工作2 h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
解:设1台大收割机和1台小收割机每小时各收割小麦x hm2和y hm2. 根据两种工作方式中的相等关系,
得方程组
去括号,得
②- ①,得11x=4.4.
解这个方程,得x=0.4.
把x=0.4代入①,得y=0.2.
因此,这个方程组的解是
答:1台大收割机和1台小收割机每小时各收割小麦0.4 hm2和0.2 hm2.
知识拓展
1.对于比较复杂的二元一次方程组,应先化简(去分母、去括号、移项、合并同类项等),通常要把每个方程整理成含有未知数的项在方程的左边,常数项在方程的右边的形式.
2.当方程组比较复杂时,应通过去分母、去括号、移项、合并同类项等,使之化为 的形式(同类项对齐),为加减消元创造有利条件.
知识拓展
3.用加减法解二元一次方程组适合于同一未知数的系数成整数倍数的情形,如果不成整数倍,那么可以将两个方程都乘一个适当的数,便于加减,另外,如果系数是分数的形式,那么要整理成 的形式,再选择适当的方法求解.
课堂小结
课堂小结
解二元一次方程组:
(1)
(6)
(5)
(3)
(4)
(2)
1.已知方程组 的解为 则2a- 3b的值为 ( )
A.4 B.6 C.- 6 D.- 4
解析: 把代入原方程组,得 用加减消元
法解得 2a- 3b=2× - 3×(- 1)=6.故选B.
检测反馈
B
2.解以下两个方程组,较为简便的是( )
A.(1)(2)均用代入法 B.(1)(2)均用加减法
C.(1)用代入法,(2)用加减法 D.(1)用加减法,(2)用代入法
解析: (1)中的第一个方程是用x表示y的形式,用代入法解答合适;(2)中的未知数t的系数互为相反数,用加减法比较合适.故选C.
C
解:原方程组可化为
①×2+②得11x=22,∴x=2,
把x=2代入①得y=3.
∴方程组的解为
解方程组
4.王大伯承包了25亩土地,今年春季改种茄子和西红柿两种大棚蔬菜,总支出44000元.其中种茄子每亩支出1700元,每亩获纯利2400元;种西红柿每亩支出1800元,每亩获纯利2600元.王大伯一共获纯利多少元?
解:设王大伯种了x亩茄子,y亩西红柿,根据题意,得
解得
一共获纯利:2400×10+2600×15=63000(元).
答:王大伯一共获纯利63000元.
