苏科版数学七上第2章 有理数的基本概念 复习课课件(22张)
文档属性
| 名称 | 苏科版数学七上第2章 有理数的基本概念 复习课课件(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 592.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 13:42:41 | ||
图片预览





文档简介
(共22张PPT)
有理数的基本概念
【要点梳理】
1.正数和负数表示一对意义相反的量.
如果运进60吨记作+60吨,那么运出40吨记作________.
前进与后退,收入与支出,增加与减少,输入与输出,上升与下降,盈利与亏损等等.
2.0既不是正数也不是负数.
指出下列数中的正数、负数:
+7,-9,,-4.5,998,0,.
答:正数: ;负数: .
0是正数、负数的分界点
【要点梳理】
正整数、负整数、零统称为整数.
正分数、负分数统称为分数.
整数和分数统称为有理数.
我们把能够写成分数形式(m、n是整数,n≠0)的数叫做有理数.有限小数和(无限)循环小数都可以化为分数,它们都是有理数.
无限不循环小数叫做无理数.
【要点梳理】
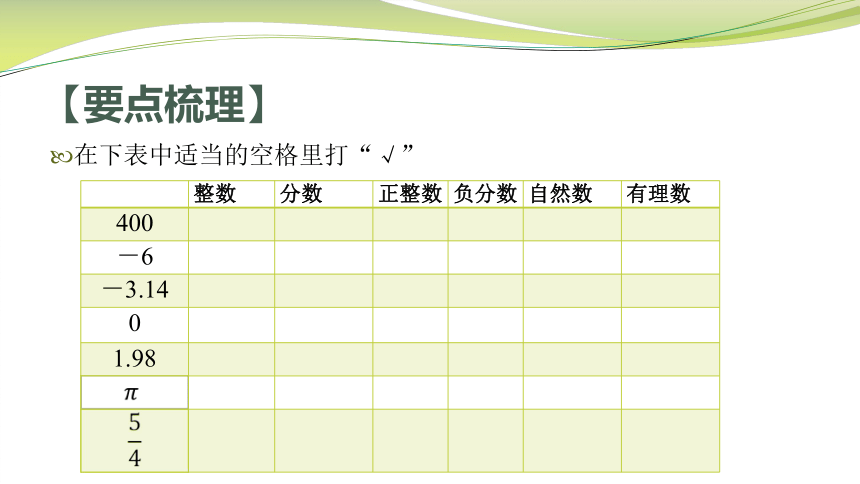
在下表中适当的空格里打“√”
? 整数 分数 正整数 负分数 自然数 有理数
400 ? ? ? ? ? ?
-6 ? ? ? ? ? ?
-3.14 ? ? ? ? ? ?
0 ? ? ? ? ? ?
1.98 ? ? ? ? ? ?
? ? ? ? ? ?
? ? ? ? ? ?
【要点梳理】
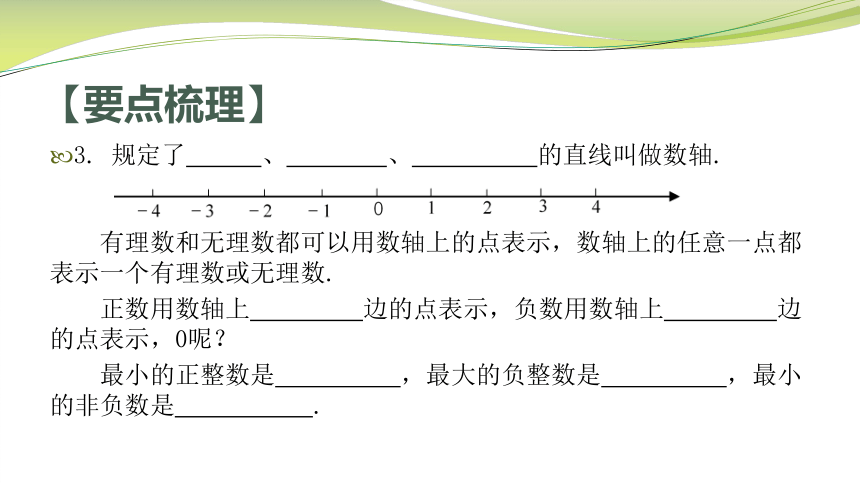
3. 规定了 、 、 的直线叫做数轴.
有理数和无理数都可以用数轴上的点表示,数轴上的任意一点都表示一个有理数或无理数.
正数用数轴上 边的点表示,负数用数轴上 边的点表示,0呢?
最小的正整数是 ,最大的负整数是 ,最小的非负数是 .
【要点梳理】
4.数轴上点A、B的位置如图所示,若点A,B表示的数分别为a,b,则a b.(填“>”“<”或“=”)
在数轴上表示的两个数,右边的数比左边的数 .
A
B
【要点梳理】
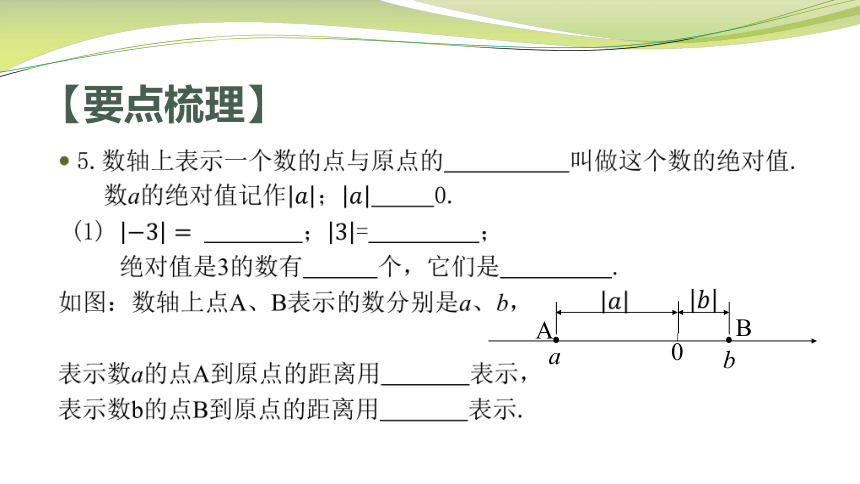
5.数轴上表示一个数的点与原点的 叫做这个数的绝对值.
数a的绝对值记作; 0.
(1) ;= ;
绝对值是3的数有 个,它们是 .
如图:数轴上点A、B表示的数分别是a、b,
表示数a的点A到原点的距离用 表示,
表示数b的点B到原点的距离用 表示.
A
a
0
B
b
【要点梳理】
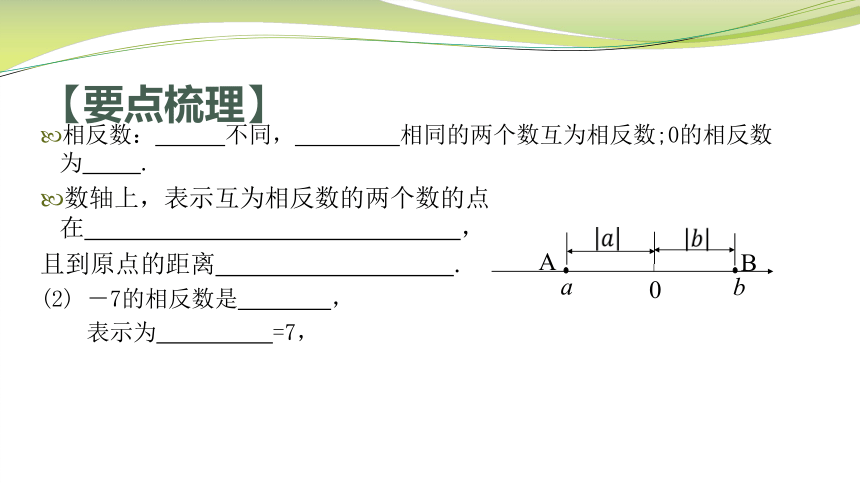
相反数: 不同, 相同的两个数互为相反数;0的相反数为 .
数轴上,表示互为相反数的两个数的点在 ,
且到原点的距离 .
(2) -7的相反数是 ,
表示为 =7,
A
a
0
B
b
.
【要点梳理】
当a>0时,= ;即正数的绝对值是 ;
当a=0时,= ;即0的绝对值是 ;
当a<0时,= . 即负数的绝对值是 .
【要点梳理】
(3) 为1的两个数互为倒数.
相反数等于本身的数是 ;倒数等于本身的数是 ;绝对值最小的数是 ;
若=a,则a ;即绝对值等于本身的数是 ;
若=-a,则a ;即绝对值等于它的相反数的数是 .
6.两个正数,绝对值大的正数大;两个负数,绝对值大的负数 .
【典型例题】
例1 把下列各数分别填入相应的大括号内:
-7,3.5,-3.1415,0,,0.03,,10,,, 0.151151115…(相邻的两个5之间1的个数一次加1),.
整数集合:{ …}
正分数集合:{ …}
非正数集合:{ …}
负有理数集合:{ …}
无理数集合:{ …}
【典型例题】
变式1 将下列各数分别填入相应的圈内:,5,0,1.5,+2,-3;
正数集合
整数集合
…
…
…
【典型例题】
变式2 已知有A、B、C三个数集,每个数集中所包含的数都写在各自的大括号内,A={-2, -3, -8,6,7},B={-3, -5,1,2,6},C={-1, -3, -8,2,5},请把这些数填在图中相应的位置.
C
A
B
【典型例题】
例2 已知有理数a,-2,b在数轴上的位置如图所示,请将a,-2,b及a,-2,b的相反数在数轴上表示出来,并将这6个数用“<”连接起来.
0
b
a
-2
【典型例题】
例3 化简:
(1)-(+4) (2)―[+(―7.1)] (3) +{-[-]} (4) -
【典型例题】
例4 如图,数轴上每相邻两点相距1个单位长度,点A、B、C、D对应的数分别是整数a、b、c、d,且b-2a=3c+d+21,那么数轴上表示原点的对应点是哪一个呢?
B
C
D
A
【典型例题】
例5 设数轴上的两个点A、B表示的数分别是a、b.
(1)若,试求a、b的值;
(2)若,借助数轴试求A、B两点之间的距离.
【典型例题】
变式1 用字母a表示一个有理数,则一定是非负数,也就是它的值为正数或0,所以的最小值为0,而一定是非正数,即它的值为负数或0,所以有最大值0,根据这个结论完成下列问题:
(1) 有最 值是 ;
(2) 有最 值是 ;
(3) 当a的值为 时,有最 值是 .
【巩固练习】
1.-0.5的倒数是 ;的绝对值是 .
2. 如图,数轴上有O、A、B三点,点O对应原点,点A对应的数为﹣1,若OB=3OA,则点B对应的数为 .
3.已知a,b,c三个数在数轴上对应点的位置如图所示,下列几个判断:①a0;④c-a<0.其中错误的个数是( )
A.1 B.2
C.3 D.4
0
a
c
b
【巩固练习】
4.按下列程序进行计算,经过三次输入,最后输出的数是10,则最初输入的数是( )
A. 4 B. C. D.
输入
×4
-6
输出
>6
No
?
Yes
?
【巩固练习】
5. 七年级一班某次数学测验的平均成绩为80分,数学老师以平均成绩为基准,记作0,把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10,–15,0,+20,–2.问这五位同学的实际成绩分别是多少分?
【巩固练习】
6.某企业生产瓶装食用调和油,根据质量要求,净含量(不含包装)可以有0.002L的误差.现抽查6瓶食用调和油,超过规定净含量的升数记作正数,不足规定净含量的升数记作负数.检查结果如下表(单位:L):
请用所学知识来说明:
(1)哪几瓶是符合要求的(即在误差范围内)?
(2)哪一瓶净含量最接近规定的净含量?
第1瓶 第2瓶 第3瓶 第4瓶 第5瓶 第6瓶
+0.0018 -0.0023 +0.0025 -0.0015 +0.0012 +0.0010
有理数的基本概念
【要点梳理】
1.正数和负数表示一对意义相反的量.
如果运进60吨记作+60吨,那么运出40吨记作________.
前进与后退,收入与支出,增加与减少,输入与输出,上升与下降,盈利与亏损等等.
2.0既不是正数也不是负数.
指出下列数中的正数、负数:
+7,-9,,-4.5,998,0,.
答:正数: ;负数: .
0是正数、负数的分界点
【要点梳理】
正整数、负整数、零统称为整数.
正分数、负分数统称为分数.
整数和分数统称为有理数.
我们把能够写成分数形式(m、n是整数,n≠0)的数叫做有理数.有限小数和(无限)循环小数都可以化为分数,它们都是有理数.
无限不循环小数叫做无理数.
【要点梳理】
在下表中适当的空格里打“√”
? 整数 分数 正整数 负分数 自然数 有理数
400 ? ? ? ? ? ?
-6 ? ? ? ? ? ?
-3.14 ? ? ? ? ? ?
0 ? ? ? ? ? ?
1.98 ? ? ? ? ? ?
? ? ? ? ? ?
? ? ? ? ? ?
【要点梳理】
3. 规定了 、 、 的直线叫做数轴.
有理数和无理数都可以用数轴上的点表示,数轴上的任意一点都表示一个有理数或无理数.
正数用数轴上 边的点表示,负数用数轴上 边的点表示,0呢?
最小的正整数是 ,最大的负整数是 ,最小的非负数是 .
【要点梳理】
4.数轴上点A、B的位置如图所示,若点A,B表示的数分别为a,b,则a b.(填“>”“<”或“=”)
在数轴上表示的两个数,右边的数比左边的数 .
A
B
【要点梳理】
5.数轴上表示一个数的点与原点的 叫做这个数的绝对值.
数a的绝对值记作; 0.
(1) ;= ;
绝对值是3的数有 个,它们是 .
如图:数轴上点A、B表示的数分别是a、b,
表示数a的点A到原点的距离用 表示,
表示数b的点B到原点的距离用 表示.
A
a
0
B
b
【要点梳理】
相反数: 不同, 相同的两个数互为相反数;0的相反数为 .
数轴上,表示互为相反数的两个数的点在 ,
且到原点的距离 .
(2) -7的相反数是 ,
表示为 =7,
A
a
0
B
b
.
【要点梳理】
当a>0时,= ;即正数的绝对值是 ;
当a=0时,= ;即0的绝对值是 ;
当a<0时,= . 即负数的绝对值是 .
【要点梳理】
(3) 为1的两个数互为倒数.
相反数等于本身的数是 ;倒数等于本身的数是 ;绝对值最小的数是 ;
若=a,则a ;即绝对值等于本身的数是 ;
若=-a,则a ;即绝对值等于它的相反数的数是 .
6.两个正数,绝对值大的正数大;两个负数,绝对值大的负数 .
【典型例题】
例1 把下列各数分别填入相应的大括号内:
-7,3.5,-3.1415,0,,0.03,,10,,, 0.151151115…(相邻的两个5之间1的个数一次加1),.
整数集合:{ …}
正分数集合:{ …}
非正数集合:{ …}
负有理数集合:{ …}
无理数集合:{ …}
【典型例题】
变式1 将下列各数分别填入相应的圈内:,5,0,1.5,+2,-3;
正数集合
整数集合
…
…
…
【典型例题】
变式2 已知有A、B、C三个数集,每个数集中所包含的数都写在各自的大括号内,A={-2, -3, -8,6,7},B={-3, -5,1,2,6},C={-1, -3, -8,2,5},请把这些数填在图中相应的位置.
C
A
B
【典型例题】
例2 已知有理数a,-2,b在数轴上的位置如图所示,请将a,-2,b及a,-2,b的相反数在数轴上表示出来,并将这6个数用“<”连接起来.
0
b
a
-2
【典型例题】
例3 化简:
(1)-(+4) (2)―[+(―7.1)] (3) +{-[-]} (4) -
【典型例题】
例4 如图,数轴上每相邻两点相距1个单位长度,点A、B、C、D对应的数分别是整数a、b、c、d,且b-2a=3c+d+21,那么数轴上表示原点的对应点是哪一个呢?
B
C
D
A
【典型例题】
例5 设数轴上的两个点A、B表示的数分别是a、b.
(1)若,试求a、b的值;
(2)若,借助数轴试求A、B两点之间的距离.
【典型例题】
变式1 用字母a表示一个有理数,则一定是非负数,也就是它的值为正数或0,所以的最小值为0,而一定是非正数,即它的值为负数或0,所以有最大值0,根据这个结论完成下列问题:
(1) 有最 值是 ;
(2) 有最 值是 ;
(3) 当a的值为 时,有最 值是 .
【巩固练习】
1.-0.5的倒数是 ;的绝对值是 .
2. 如图,数轴上有O、A、B三点,点O对应原点,点A对应的数为﹣1,若OB=3OA,则点B对应的数为 .
3.已知a,b,c三个数在数轴上对应点的位置如图所示,下列几个判断:①a
A.1 B.2
C.3 D.4
0
a
c
b
【巩固练习】
4.按下列程序进行计算,经过三次输入,最后输出的数是10,则最初输入的数是( )
A. 4 B. C. D.
输入
×4
-6
输出
>6
No
?
Yes
?
【巩固练习】
5. 七年级一班某次数学测验的平均成绩为80分,数学老师以平均成绩为基准,记作0,把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10,–15,0,+20,–2.问这五位同学的实际成绩分别是多少分?
【巩固练习】
6.某企业生产瓶装食用调和油,根据质量要求,净含量(不含包装)可以有0.002L的误差.现抽查6瓶食用调和油,超过规定净含量的升数记作正数,不足规定净含量的升数记作负数.检查结果如下表(单位:L):
请用所学知识来说明:
(1)哪几瓶是符合要求的(即在误差范围内)?
(2)哪一瓶净含量最接近规定的净含量?
第1瓶 第2瓶 第3瓶 第4瓶 第5瓶 第6瓶
+0.0018 -0.0023 +0.0025 -0.0015 +0.0012 +0.0010
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
