北师大版八年级数学下册4.3 公式法(2)完全平方公式课件(共33张PPT)
文档属性
| 名称 | 北师大版八年级数学下册4.3 公式法(2)完全平方公式课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 983.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 09:40:32 | ||
图片预览










文档简介
课件33张PPT。
因式分解温故知新分解因式4x2-9=(2x)2-32=(2x+3)(2x-3)能用平方差公式进行因式分解的多项式有
什么特点?
下面的多项式能用平方差公式分解因式吗?
(1) a2+2ab+b2 (2) a2-2ab+b2
(1)两项 (2)平方差a2 +2ab+ b2 = (a+b)2
a2 -2ab+ b2 = (a-b)2
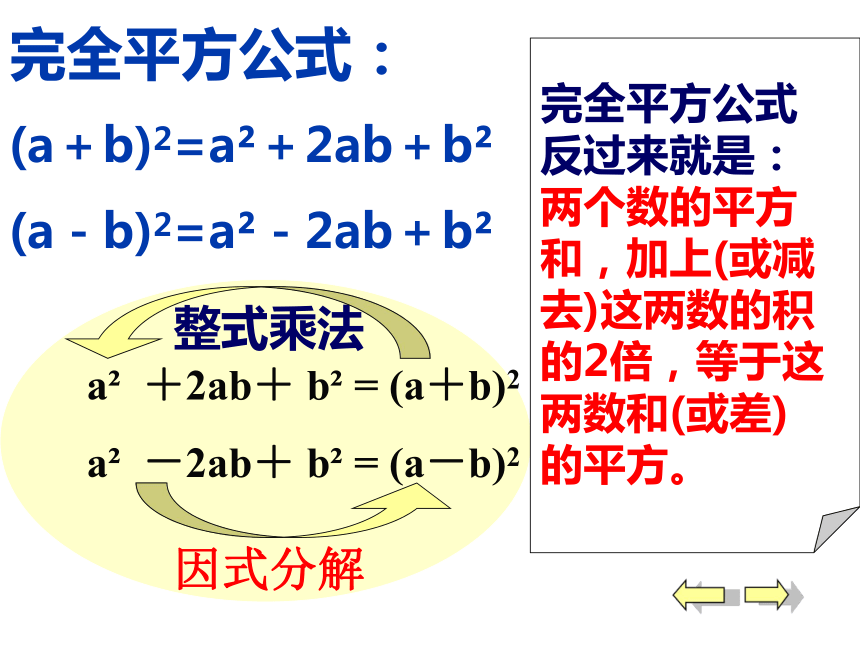
完全平方公式反过来就是:两个数的平方和,加上(或减去)这两数的积的2倍,等于这两数和(或差)的平方。因式分解完全平方公式:
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2整式乘法一、新课引入试计算:9992 + 1998 + 12×999×1= (999+1)2 = 106此处运用了什么公式?
完全平方公式逆用 就像平方差公式一样,完全平方公式也可以逆用,从而进行一些简便计算与因式分解。
即:完全平方式的特点:
1、必须是三项式(或可以看成三项的)
2、有两个同号的平方项
3、有一个乘积项(等于平方项底数的±2倍)
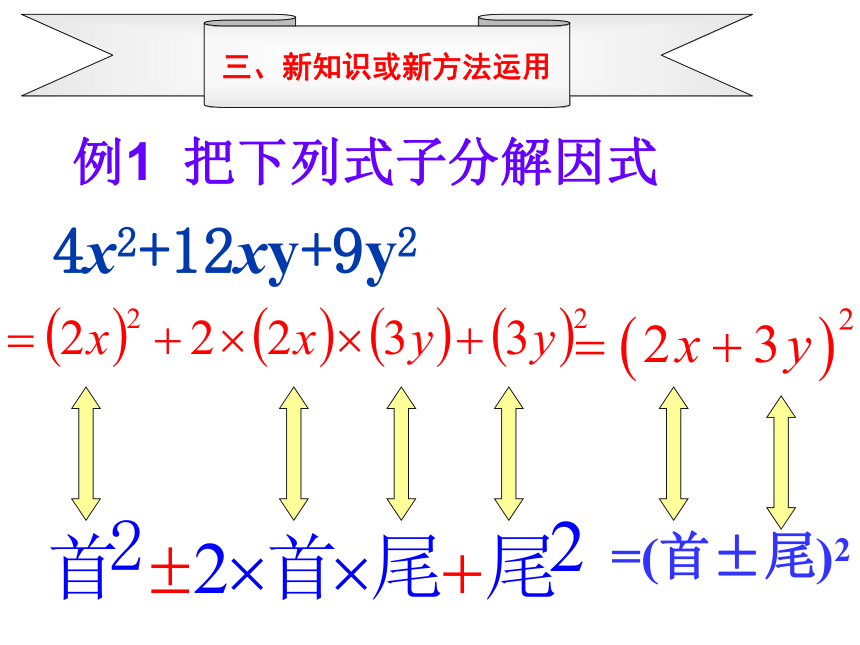
简记口诀:首平方,尾平方,首尾两倍在中央。二.完全平方式 =(a±b)2 a2±2ab+b2完全平方公式:我们把以上两个式子叫做完全平方式头平方,尾平方,头尾两倍中间放. =(a+b)2 a2+2ab+b2 =(a -b)2 a2- 2ab+b2 简记口诀1.判别下列各式能否运用完全平方式分解因式.不能能能不能能扎实基础2、下列各式是不是完全平方式是是是否是否3、请补上一项,使下列多项式成为完全平方式例1 把下列式子分解因式4x2+12xy+9y2三、新知识或新方法运用·例2 分解因式:(1) 16x2+24x+916x2+24x+9=(4x)2+2·4x·3 +32a22abb2+·+解:(1)16x2+24x+9三、新知识或新方法运用∴16x2+24x+9是一个完全平方式分析:=(4x)2+2·4x·3+32=(4x+3)2.例2 分解因式:(2) –x2+4xy–4y2.解:(2) –x2+4xy-4y2
= -(x2-4xy+4y2)
= -[x2-2·x·2y+(2y)2]
= - (x-2y)2 三、新知识或新方法运用例3 分解因式: (1) 3ax2+6axy+3ay2; 分析:在(1)中有公因式3a,应先提出公因式,再进一步分解。解:(1)3ax2+6axy+3ay2
=3a(x2+2xy+y2)
=3a(x+y)2(2)(a+b)2-12(a+b)+36
=(a+b)2-2·(a+b)·6+62
=(a+b-6)2.三、新知识或新方法运用 (2) (a+b)2-12(a+b)+36.例4 把下列各式分解因式:x4-2x2+1 =(x2-1)2=(x+1)2(x-1)2=[ (9x2 ) -4y2] 2=(3x+2y)2(3x-2y)2= (x2 +y2+2xy)(x2+y2-2xy)= (x+ y)2 (x-y)2= (a2 +4+4a)(a2+4-4a)= (a+ 2)2 (a-2)2(2)(x2+y2)2-4x2y2 (4)(a2+4)2-16a2=[(x+1)(x-1)]2=[(3x+2y)(3x-2y)]2 (3)81x4-72x2y2+16y41、如何用符号表示完全平方公式?2、完全平方公式的结构特点是什么?四、小结1、必须是三项式(或可以看成三项的)
2、有两个同号的平方项
3、有一个乘积项(等于平方项底数的±2倍)
口诀: =(a+b)2 a2+2ab+b2 =(a -b)2 a2- 2ab+b2首平方,尾平方,首尾两倍在中央,得到首尾和(差)的平方。练习:因式分解练习:因式分解例5.用简便方法运算。例4 把下列各式分解因式:x4-2x2+1 =(x2-1)2=(x+1)2(x-1)2=[ (9x2 ) -4y2] 2=(3x+2y)2(3x-2y)2= (x2 +y2+2xy)(x2+y2-2xy)= (x+ y)2 (x-y)2= (a2 +4+4a)(a2+4-4a)= (a+ 2)2 (a-2)2(2)(x2+y2)2-4x2y2 (4)(a2+4)2-16a2=[(x+1)(x-1)]2=[(3x+2y)(3x-2y)]2 (3)81x4-72x2y2+16y4例5 把下列各式分解因式:2x2+2x+ = (4x2+4x+1)= (2x+1)2(2)(x+1)(x+2)+ 先观察是否有公因式,若有公因式提出后看是否具有平方差公式或完全平方公式特征,若有使用公式法;若没有,则考虑将多项式进行重新整理或分组后进行分解因式。=x2+3x+2+=x2+3x+=(x+ )2拓展与提高1.已知a、b、c是三角形的三边,请你判断
a2-b2-c2-2bc的值的正负.解: a2-b2-c2-2bc=a2-(b+c)2=(a-b-c)(a+b+c)∵ a-b-c<0,a+b+c﹥0∴ (a-b-c)(a+b+c) <0∴ a2-b2-c2-2bc的值为负.
2.将 再加上一个单项式,使它成为一个多项式平方,你有几种方法?±4x,4x44x2±4x+1=(2x±1)24x4±4x2+1=(2x2±1)2拓展与提高3.一天,小明在纸上写了一个算式为 4x2 +8x+11,并对小刚说:“无论x取何值,这个代数式的值都是正值,你不信试一试?”解:拓展与提高4x2+8x+11=4(x2+2x)+11=4(x2+2x+1-1)+11=4(x+1)2-4+11=4(x+1)2+7∵4(x+1)2≥0即4x2+8x+11>0,所以小刚说得对.∴4(x+1)2+7>01.如果多项式x2+2mx+4是完全平方式,求m的值.拓展创新竞赛与拓展已知a-b=1,b-c=2,请你利用完全平方公式求值:a2+b2+c2-ab-bc-ca的值.再见1.下列各式是不是完全平方式? (1) a2-4a+4 ( )
(2) a2+4a+16 ( )
(3) a2-8a+16 ( )
(4) a2-6a-9 ( )
(5) a2+ ( )√×√××课后巩固 练习
1.下列多项式是不是完全平方式?为什么?
(1) a2-4a+4; (2)1+4a2;
(3) 4b2+4b-1 ; (4)a2+ab+b2.2.分解因式:
(1) x2+12x+36; (2) -2xy-x2-y2;
(3) a2+2a+1; (4) 4x2-4x+1;
(5) ax2+2a2x+a3; (6) -3x2+6xy-3y2.课本P :119 习题14.3
第3、9题。五、作业1. 用简便方法计算:联系拓广例题出击灵活地把(a+b)看成一个整体,这需要你的智慧哟。 例1 把下列各式分解因式:
16a2+24a +9
-x2+4xy-4y2
3ax2+6axy+3ay2
(a+b) 2-12 (a+b)+36
注意啦!首先要考虑能不能提取公因式!
因式分解温故知新分解因式4x2-9=(2x)2-32=(2x+3)(2x-3)能用平方差公式进行因式分解的多项式有
什么特点?
下面的多项式能用平方差公式分解因式吗?
(1) a2+2ab+b2 (2) a2-2ab+b2
(1)两项 (2)平方差a2 +2ab+ b2 = (a+b)2
a2 -2ab+ b2 = (a-b)2
完全平方公式反过来就是:两个数的平方和,加上(或减去)这两数的积的2倍,等于这两数和(或差)的平方。因式分解完全平方公式:
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2整式乘法一、新课引入试计算:9992 + 1998 + 12×999×1= (999+1)2 = 106此处运用了什么公式?
完全平方公式逆用 就像平方差公式一样,完全平方公式也可以逆用,从而进行一些简便计算与因式分解。
即:完全平方式的特点:
1、必须是三项式(或可以看成三项的)
2、有两个同号的平方项
3、有一个乘积项(等于平方项底数的±2倍)
简记口诀:首平方,尾平方,首尾两倍在中央。二.完全平方式 =(a±b)2 a2±2ab+b2完全平方公式:我们把以上两个式子叫做完全平方式头平方,尾平方,头尾两倍中间放. =(a+b)2 a2+2ab+b2 =(a -b)2 a2- 2ab+b2 简记口诀1.判别下列各式能否运用完全平方式分解因式.不能能能不能能扎实基础2、下列各式是不是完全平方式是是是否是否3、请补上一项,使下列多项式成为完全平方式例1 把下列式子分解因式4x2+12xy+9y2三、新知识或新方法运用·例2 分解因式:(1) 16x2+24x+916x2+24x+9=(4x)2+2·4x·3 +32a22abb2+·+解:(1)16x2+24x+9三、新知识或新方法运用∴16x2+24x+9是一个完全平方式分析:=(4x)2+2·4x·3+32=(4x+3)2.例2 分解因式:(2) –x2+4xy–4y2.解:(2) –x2+4xy-4y2
= -(x2-4xy+4y2)
= -[x2-2·x·2y+(2y)2]
= - (x-2y)2 三、新知识或新方法运用例3 分解因式: (1) 3ax2+6axy+3ay2; 分析:在(1)中有公因式3a,应先提出公因式,再进一步分解。解:(1)3ax2+6axy+3ay2
=3a(x2+2xy+y2)
=3a(x+y)2(2)(a+b)2-12(a+b)+36
=(a+b)2-2·(a+b)·6+62
=(a+b-6)2.三、新知识或新方法运用 (2) (a+b)2-12(a+b)+36.例4 把下列各式分解因式:x4-2x2+1 =(x2-1)2=(x+1)2(x-1)2=[ (9x2 ) -4y2] 2=(3x+2y)2(3x-2y)2= (x2 +y2+2xy)(x2+y2-2xy)= (x+ y)2 (x-y)2= (a2 +4+4a)(a2+4-4a)= (a+ 2)2 (a-2)2(2)(x2+y2)2-4x2y2 (4)(a2+4)2-16a2=[(x+1)(x-1)]2=[(3x+2y)(3x-2y)]2 (3)81x4-72x2y2+16y41、如何用符号表示完全平方公式?2、完全平方公式的结构特点是什么?四、小结1、必须是三项式(或可以看成三项的)
2、有两个同号的平方项
3、有一个乘积项(等于平方项底数的±2倍)
口诀: =(a+b)2 a2+2ab+b2 =(a -b)2 a2- 2ab+b2首平方,尾平方,首尾两倍在中央,得到首尾和(差)的平方。练习:因式分解练习:因式分解例5.用简便方法运算。例4 把下列各式分解因式:x4-2x2+1 =(x2-1)2=(x+1)2(x-1)2=[ (9x2 ) -4y2] 2=(3x+2y)2(3x-2y)2= (x2 +y2+2xy)(x2+y2-2xy)= (x+ y)2 (x-y)2= (a2 +4+4a)(a2+4-4a)= (a+ 2)2 (a-2)2(2)(x2+y2)2-4x2y2 (4)(a2+4)2-16a2=[(x+1)(x-1)]2=[(3x+2y)(3x-2y)]2 (3)81x4-72x2y2+16y4例5 把下列各式分解因式:2x2+2x+ = (4x2+4x+1)= (2x+1)2(2)(x+1)(x+2)+ 先观察是否有公因式,若有公因式提出后看是否具有平方差公式或完全平方公式特征,若有使用公式法;若没有,则考虑将多项式进行重新整理或分组后进行分解因式。=x2+3x+2+=x2+3x+=(x+ )2拓展与提高1.已知a、b、c是三角形的三边,请你判断
a2-b2-c2-2bc的值的正负.解: a2-b2-c2-2bc=a2-(b+c)2=(a-b-c)(a+b+c)∵ a-b-c<0,a+b+c﹥0∴ (a-b-c)(a+b+c) <0∴ a2-b2-c2-2bc的值为负.
2.将 再加上一个单项式,使它成为一个多项式平方,你有几种方法?±4x,4x44x2±4x+1=(2x±1)24x4±4x2+1=(2x2±1)2拓展与提高3.一天,小明在纸上写了一个算式为 4x2 +8x+11,并对小刚说:“无论x取何值,这个代数式的值都是正值,你不信试一试?”解:拓展与提高4x2+8x+11=4(x2+2x)+11=4(x2+2x+1-1)+11=4(x+1)2-4+11=4(x+1)2+7∵4(x+1)2≥0即4x2+8x+11>0,所以小刚说得对.∴4(x+1)2+7>01.如果多项式x2+2mx+4是完全平方式,求m的值.拓展创新竞赛与拓展已知a-b=1,b-c=2,请你利用完全平方公式求值:a2+b2+c2-ab-bc-ca的值.再见1.下列各式是不是完全平方式? (1) a2-4a+4 ( )
(2) a2+4a+16 ( )
(3) a2-8a+16 ( )
(4) a2-6a-9 ( )
(5) a2+ ( )√×√××课后巩固 练习
1.下列多项式是不是完全平方式?为什么?
(1) a2-4a+4; (2)1+4a2;
(3) 4b2+4b-1 ; (4)a2+ab+b2.2.分解因式:
(1) x2+12x+36; (2) -2xy-x2-y2;
(3) a2+2a+1; (4) 4x2-4x+1;
(5) ax2+2a2x+a3; (6) -3x2+6xy-3y2.课本P :119 习题14.3
第3、9题。五、作业1. 用简便方法计算:联系拓广例题出击灵活地把(a+b)看成一个整体,这需要你的智慧哟。 例1 把下列各式分解因式:
16a2+24a +9
-x2+4xy-4y2
3ax2+6axy+3ay2
(a+b) 2-12 (a+b)+36
注意啦!首先要考虑能不能提取公因式!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
