北师大版数学八年级下册第三章《平移与旋转》回顾与思考课件(共55张PPT)
文档属性
| 名称 | 北师大版数学八年级下册第三章《平移与旋转》回顾与思考课件(共55张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 09:05:02 | ||
图片预览




文档简介
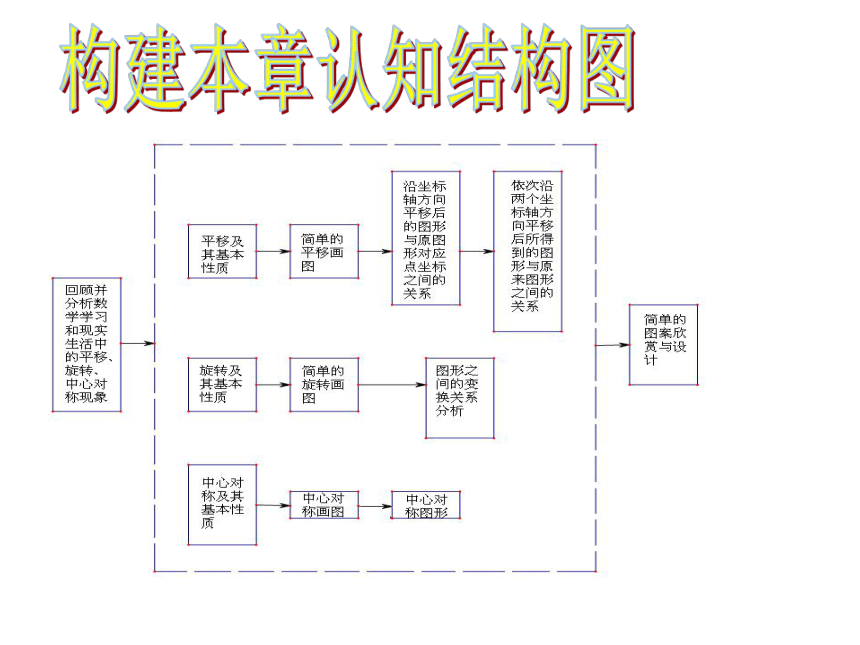
课件55张PPT。第三章 图形的平移与旋转3.5回顾与思考构建本章认知结构图一、平移
2、平移的性质:
图形平移后,对应点所连的线段平行(或在一条直线上)且相等;
对应线段平行(或在一条直线上)且相等;对应角相等。 1、平移的概念:在平面内,将一个图形沿着
某个方向移动一定的距离,这样的图形运动
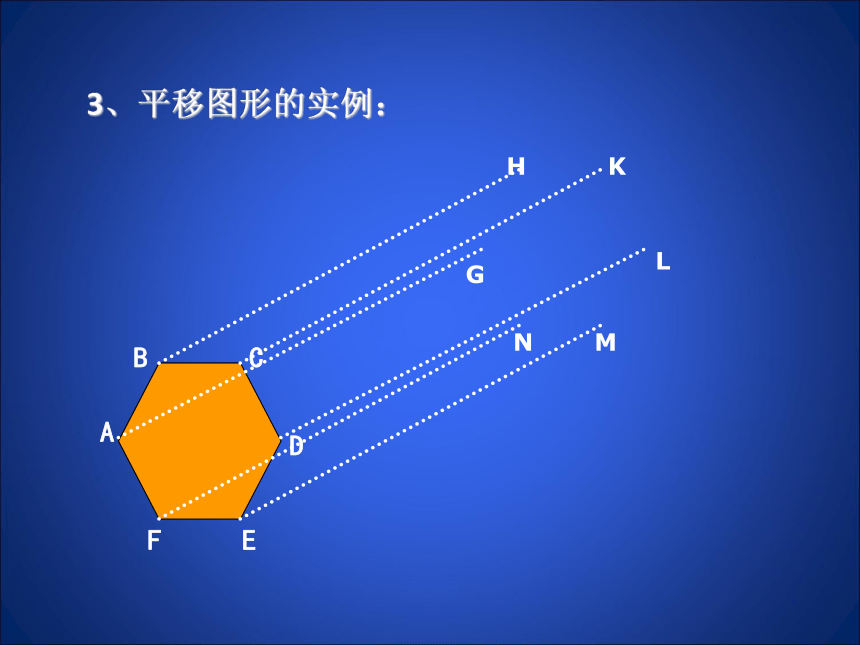
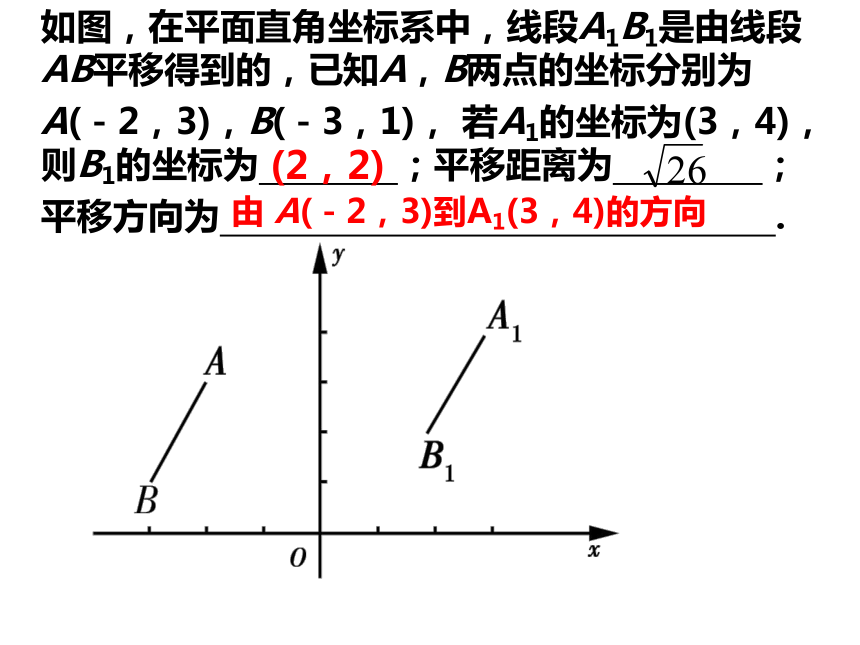
叫做图形的平移。(x+a , y)(x-a , y)(x , y+a)(x , y-a)向右平移向左平移向上平移向下平移3.平移性质 在平面直角坐标系中,一个图形沿x或y轴方向平移a(a>0)个单位长度的图形与原图形对应点的坐标之间有什么关系?设原坐标为(x , y)3、平移图形的实例:ABCDEFGHKLMN 如图,在平面直角坐标系中,线段A1B1是由线段AB平移得到的,已知A,B两点的坐标分别为
A(-2,3),B(-3,1), 若A1的坐标为(3,4),则B1的坐标为 ;平移距离为 ;
平移方向为 . (2,2)由 A(-2,3)到A1(3,4)的方向二、旋转1.旋转:在平面内,将一个图形绕一个定点按某个方向转动一定的角度,这样的图形运动叫做旋转,这个定点叫做旋转中心,旋转的角度叫做旋转角。2.旋转的性质:一个图形和它经过旋转所得图形中,(1)对应点到旋转中心的距离相等;(2)任意一对对应点与旋转中心的连线所成的角都等于旋转角;
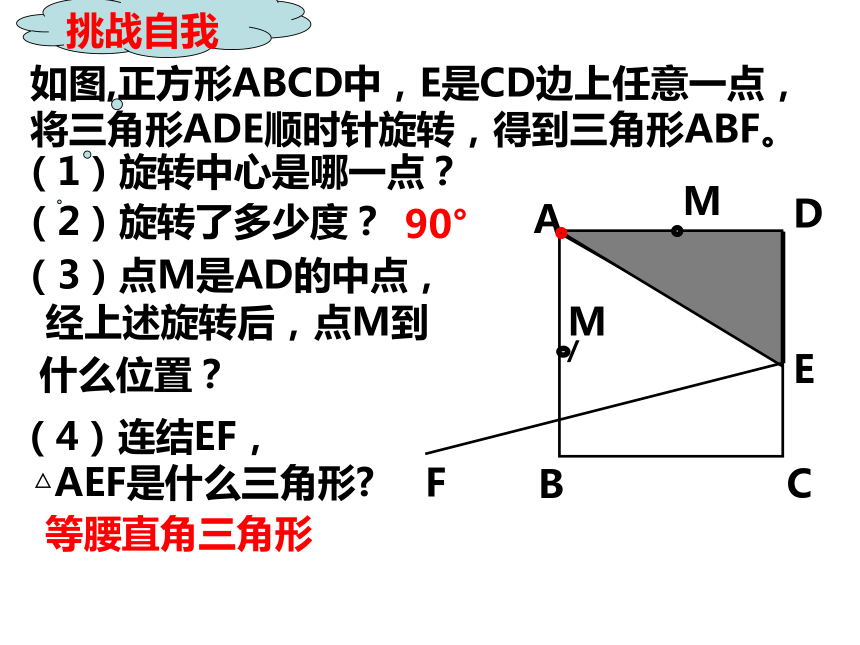
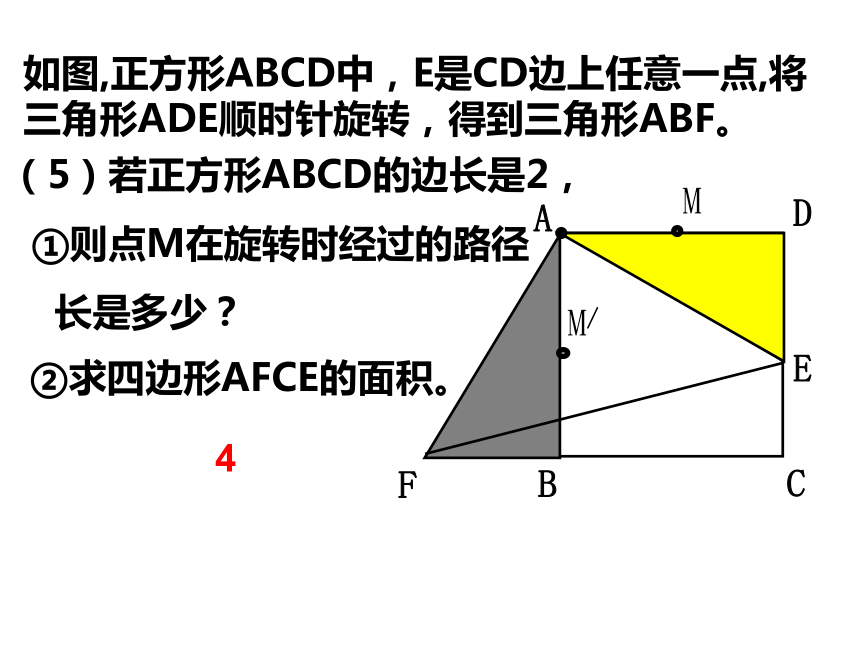
45o(3)对应线段相等,对应角相等。如图,正方形ABCD中,E是CD边上任意一点,将三角形ADE顺时针旋转,得到三角形ABF。ADCBEF(4)连结EF,(2)旋转了多少度?(1)旋转中心是哪一点?(3)点M是AD的中点, 挑战自我90°等腰直角三角形 经上述旋转后,点M到什么位置?△AEF是什么三角形?如图,正方形ABCD中,E是CD边上任意一点,将三角形ADE顺时针旋转,得到三角形ABF。ADCBEF(5)若正方形ABCD的边长是2,
①则点M在旋转时经过的路径
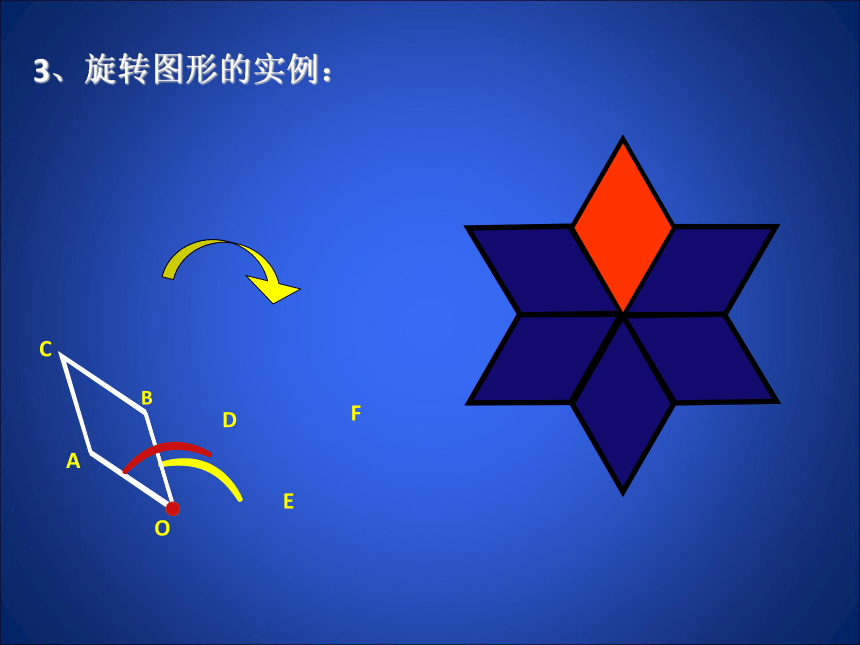
长是多少?②求四边形AFCE的面积。 43、旋转图形的实例:O︵
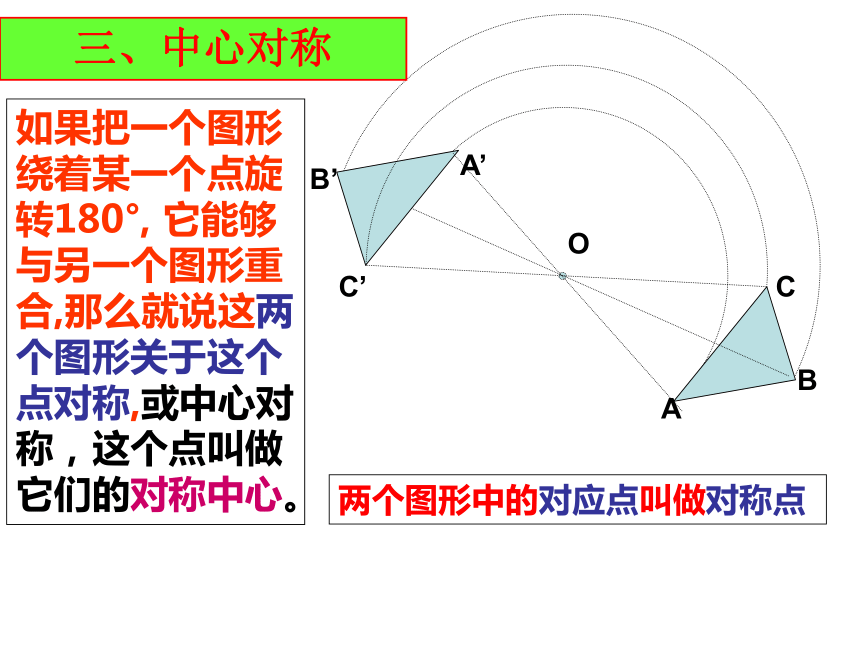
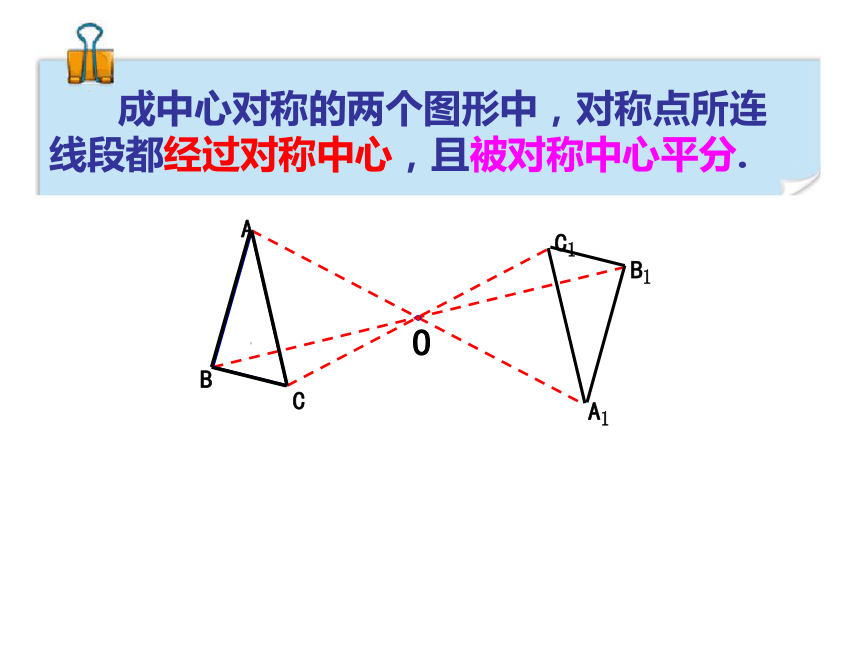
F︵ABCDE如果把一个图形绕着某一个点旋转180°, 它能够与另一个图形重合,那么就说这两个图形关于这个点对称,或中心对称,这个点叫做它们的对称中心。两个图形中的对应点叫做对称点三、中心对称 成中心对称的两个图形中,对称点所连线段都经过对称中心,且被对称中心平分.把一个图形绕某个点旋转180O后能与自身重合,我们把这种图形叫做中心对称图形,这个点叫做它的对称中心.中心对称图形的概念: 常见的轴对称图形与中心对称图形2条1条1条3条2条2条4条1条中点对角线交点对角线交点对角线交点对角线交点无无无无无AA′B′BO 2、线段的中心对称线段的作法AOA′1、点的中心对称点的作法以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
连结AO并延长到A’,使OA’=OA,
得到点A的对称点A’.四、灵活运用例1 (2)如图,选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.A′C′B′△A′B′C′即为所求的三角形。
B、B’应是对应点,用刻度尺找出BB’的中点O,则点O即为所求(如图)O确定对称中心0?方法1:一组对称点连线段的中点.OB、B’及C、C’应是两组对应点连线的交点 O ,(如图)
怎样找对称中心0?方法2:两组对称点连线的交点.四、轴对称 1.轴对称的概念:如果两个平面图形沿一条直线对折后能够完全重合,那么称这两个图形成轴对称。2.轴对称的图形实例B1C1A1改
变不
变不
变对称轴平移方向,
距离旋转中心,
方向,角度改
变不
变改
变轴对称、平移、旋转的区别及联系:轴 对 称中 心 对 称123翻转后和另一个图形重合旋转后和另一个图形重合 中心对称与轴对称的联系与区别 中心对称与中心对称图形的联系与区别区别:
中心对称指两个全等图形的相互位置关系,中心对称图形指一个图形本身成中心对称.联系:
如果将中心对称图形的两个图形看成一个整体,则它们是中心对称图形. 如果将中心对称图形对称的部分看成两个图形,则它们成中心对称.例2. P是正方形内一点,将△ ABP绕点B顺时针方向旋转至与△CBP′重合,若PB=3,求PP′的长。解:由旋转的性质可知
BP=BP′, ∠PBP=∠ABC=90°
∴ △ PBP ′是等腰直角三 角形。
∴ PP ′= 一题一练△ ABC是等边三角形,把△ ABC绕点C顺时针任意旋转一个角度得到△ A′B′C,则AA ′与BB ′之间有什么关系,你能说明理由吗?四、中心对称1、设(x,y)是原图形上的一点,经过平移后,这个点与其对应点的坐标之间有如下关系:
五、图形的平移与坐标变化之间的关系2、设(x,y)是原图形上的一点,当它沿x轴方向平移a个单位长度(a>0)、沿y轴方向平移b个单位长度(b>0)后,这个点与其对应点的坐标之间有如下关系:画一画(1)画一画(2) 如图,怎样将右边的图案变成左边的图案?说一说练习3答:以右边图案的中心为旋转中心,将图案按逆时针方向旋转90°,然后平移,即可得到左边的图案。练一练——平移、旋转、中心对称的运用练一练——平移、旋转、中心对称的运用练一练——平移、旋转、中心对称的运用练一练——平移、旋转、中心对称的运用练一练——平移、旋转、中心对称的运用 轴对称、平移、旋转是几何中的重要概念,应用轴对称、平移、旋转解题也是一种极为重要的数学思想方法,适当地应用轴对称、平移、旋转等方法,将那些分散、远离的条件从图形的某一部分转移到适当的新的位置上,集中、汇集已知条件和求证结论,发现、拓展解题思路,构造基础三角形、平行四边形,进行计算与证明。方法小结你能将右图通过平移或旋转,得到左图吗?想一想说一说练习1怎样将甲图案变成乙图案?甲甲乙乙ABBA可以先将甲图案绕图上的A点旋转,使得图案被“扶直”,然后,再沿AB方向将所得图案平移到B点位置,即可得到乙图案 还可以用什么方法把甲图案变成乙图案?说一说练习2 下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?平移:平移的方向?平移的距离?仅靠平移无法得到议一议旋转: 下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?议一议 整个图形可以看作是左边的两个小“十字”绕着图案的中心旋转3次,分别旋转90°、180°、270°前后图形组成的。平移、 旋转相结合:先平移后旋转 下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?议一议 整个图形可以看作是左边的两个小“十字”先通过一次平移成图形右侧的部分,然后左、右部分一起绕图形的中心旋转90°前后图形组成的。轴对称: 下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?议一议 直线EF与GH相交于图形的中心O,且互相垂直,先把左边的两个“十字”作关于EF的轴对称图形,然后作这两部分关于GH的轴对称图形,这样就可以得到整个图形。O对称轴?拓展提升训练:※巧用变换思想,灵活求解面积1.如图所示的图案是一个轴对称图形(不考虑颜色),直线m是它的一条对称轴.已知图中圆的半径为r,求你能借助轴对称的方法求出图中阴影部分的面积吗?说说你的做法。m解:以直线m为对称轴,把m左边绿色部分反射到m的右边,那么它们的像恰好填补了右边的白色部分,所以图中的绿色部分面积等于半个圆的面积,也就是m2、如图所示,AB是长为4的线段,且CD⊥AB于O。你能借助旋转的方法求出图中阴影部分的面积吗?说说你的做法。OABCD
试一试
3.如图所示,AB是长为4的线段,且CD⊥AB于O。你能借助旋转的方法求出图中阴影部分的面积吗?说说你的做法。OABCD4.如图,在△ABC中,∠BAC=1200,以BC为边向外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.
6.如图,点P是边长为a的正方形ABCD内的一点,连PA、PB、PC,且PB = b ( b(1)求旋转过程中边PA所扫过区域(图中阴影部分)的面积。
(2)若PB=3,求PP′的长。
(3)在(2)的条件下,若PA=4,
∠APB=135 °,求PC的长。
(4)若PA2+PC2=2PB2,
请说明点P必在对角线AC上。7.如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)
(图1) (图2) (图3) (图4)
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;解:(1)图形平移的距离就是线段BC的长,
又∵在Rt△ABC中,斜边长为10cm,∠BAC=300,∴BC=5cm,
∴平移的距离为5cm。(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;(图3)(图5)(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH﹦DH(图3)(图5)
2、平移的性质:
图形平移后,对应点所连的线段平行(或在一条直线上)且相等;
对应线段平行(或在一条直线上)且相等;对应角相等。 1、平移的概念:在平面内,将一个图形沿着
某个方向移动一定的距离,这样的图形运动
叫做图形的平移。(x+a , y)(x-a , y)(x , y+a)(x , y-a)向右平移向左平移向上平移向下平移3.平移性质 在平面直角坐标系中,一个图形沿x或y轴方向平移a(a>0)个单位长度的图形与原图形对应点的坐标之间有什么关系?设原坐标为(x , y)3、平移图形的实例:ABCDEFGHKLMN 如图,在平面直角坐标系中,线段A1B1是由线段AB平移得到的,已知A,B两点的坐标分别为
A(-2,3),B(-3,1), 若A1的坐标为(3,4),则B1的坐标为 ;平移距离为 ;
平移方向为 . (2,2)由 A(-2,3)到A1(3,4)的方向二、旋转1.旋转:在平面内,将一个图形绕一个定点按某个方向转动一定的角度,这样的图形运动叫做旋转,这个定点叫做旋转中心,旋转的角度叫做旋转角。2.旋转的性质:一个图形和它经过旋转所得图形中,(1)对应点到旋转中心的距离相等;(2)任意一对对应点与旋转中心的连线所成的角都等于旋转角;
45o(3)对应线段相等,对应角相等。如图,正方形ABCD中,E是CD边上任意一点,将三角形ADE顺时针旋转,得到三角形ABF。ADCBEF(4)连结EF,(2)旋转了多少度?(1)旋转中心是哪一点?(3)点M是AD的中点, 挑战自我90°等腰直角三角形 经上述旋转后,点M到什么位置?△AEF是什么三角形?如图,正方形ABCD中,E是CD边上任意一点,将三角形ADE顺时针旋转,得到三角形ABF。ADCBEF(5)若正方形ABCD的边长是2,
①则点M在旋转时经过的路径
长是多少?②求四边形AFCE的面积。 43、旋转图形的实例:O︵
F︵ABCDE如果把一个图形绕着某一个点旋转180°, 它能够与另一个图形重合,那么就说这两个图形关于这个点对称,或中心对称,这个点叫做它们的对称中心。两个图形中的对应点叫做对称点三、中心对称 成中心对称的两个图形中,对称点所连线段都经过对称中心,且被对称中心平分.把一个图形绕某个点旋转180O后能与自身重合,我们把这种图形叫做中心对称图形,这个点叫做它的对称中心.中心对称图形的概念: 常见的轴对称图形与中心对称图形2条1条1条3条2条2条4条1条中点对角线交点对角线交点对角线交点对角线交点无无无无无AA′B′BO 2、线段的中心对称线段的作法AOA′1、点的中心对称点的作法以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
连结AO并延长到A’,使OA’=OA,
得到点A的对称点A’.四、灵活运用例1 (2)如图,选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.A′C′B′△A′B′C′即为所求的三角形。
B、B’应是对应点,用刻度尺找出BB’的中点O,则点O即为所求(如图)O确定对称中心0?方法1:一组对称点连线段的中点.OB、B’及C、C’应是两组对应点连线的交点 O ,(如图)
怎样找对称中心0?方法2:两组对称点连线的交点.四、轴对称 1.轴对称的概念:如果两个平面图形沿一条直线对折后能够完全重合,那么称这两个图形成轴对称。2.轴对称的图形实例B1C1A1改
变不
变不
变对称轴平移方向,
距离旋转中心,
方向,角度改
变不
变改
变轴对称、平移、旋转的区别及联系:轴 对 称中 心 对 称123翻转后和另一个图形重合旋转后和另一个图形重合 中心对称与轴对称的联系与区别 中心对称与中心对称图形的联系与区别区别:
中心对称指两个全等图形的相互位置关系,中心对称图形指一个图形本身成中心对称.联系:
如果将中心对称图形的两个图形看成一个整体,则它们是中心对称图形. 如果将中心对称图形对称的部分看成两个图形,则它们成中心对称.例2. P是正方形内一点,将△ ABP绕点B顺时针方向旋转至与△CBP′重合,若PB=3,求PP′的长。解:由旋转的性质可知
BP=BP′, ∠PBP=∠ABC=90°
∴ △ PBP ′是等腰直角三 角形。
∴ PP ′= 一题一练△ ABC是等边三角形,把△ ABC绕点C顺时针任意旋转一个角度得到△ A′B′C,则AA ′与BB ′之间有什么关系,你能说明理由吗?四、中心对称1、设(x,y)是原图形上的一点,经过平移后,这个点与其对应点的坐标之间有如下关系:
五、图形的平移与坐标变化之间的关系2、设(x,y)是原图形上的一点,当它沿x轴方向平移a个单位长度(a>0)、沿y轴方向平移b个单位长度(b>0)后,这个点与其对应点的坐标之间有如下关系:画一画(1)画一画(2) 如图,怎样将右边的图案变成左边的图案?说一说练习3答:以右边图案的中心为旋转中心,将图案按逆时针方向旋转90°,然后平移,即可得到左边的图案。练一练——平移、旋转、中心对称的运用练一练——平移、旋转、中心对称的运用练一练——平移、旋转、中心对称的运用练一练——平移、旋转、中心对称的运用练一练——平移、旋转、中心对称的运用 轴对称、平移、旋转是几何中的重要概念,应用轴对称、平移、旋转解题也是一种极为重要的数学思想方法,适当地应用轴对称、平移、旋转等方法,将那些分散、远离的条件从图形的某一部分转移到适当的新的位置上,集中、汇集已知条件和求证结论,发现、拓展解题思路,构造基础三角形、平行四边形,进行计算与证明。方法小结你能将右图通过平移或旋转,得到左图吗?想一想说一说练习1怎样将甲图案变成乙图案?甲甲乙乙ABBA可以先将甲图案绕图上的A点旋转,使得图案被“扶直”,然后,再沿AB方向将所得图案平移到B点位置,即可得到乙图案 还可以用什么方法把甲图案变成乙图案?说一说练习2 下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?平移:平移的方向?平移的距离?仅靠平移无法得到议一议旋转: 下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?议一议 整个图形可以看作是左边的两个小“十字”绕着图案的中心旋转3次,分别旋转90°、180°、270°前后图形组成的。平移、 旋转相结合:先平移后旋转 下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?议一议 整个图形可以看作是左边的两个小“十字”先通过一次平移成图形右侧的部分,然后左、右部分一起绕图形的中心旋转90°前后图形组成的。轴对称: 下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?议一议 直线EF与GH相交于图形的中心O,且互相垂直,先把左边的两个“十字”作关于EF的轴对称图形,然后作这两部分关于GH的轴对称图形,这样就可以得到整个图形。O对称轴?拓展提升训练:※巧用变换思想,灵活求解面积1.如图所示的图案是一个轴对称图形(不考虑颜色),直线m是它的一条对称轴.已知图中圆的半径为r,求你能借助轴对称的方法求出图中阴影部分的面积吗?说说你的做法。m解:以直线m为对称轴,把m左边绿色部分反射到m的右边,那么它们的像恰好填补了右边的白色部分,所以图中的绿色部分面积等于半个圆的面积,也就是m2、如图所示,AB是长为4的线段,且CD⊥AB于O。你能借助旋转的方法求出图中阴影部分的面积吗?说说你的做法。OABCD
试一试
3.如图所示,AB是长为4的线段,且CD⊥AB于O。你能借助旋转的方法求出图中阴影部分的面积吗?说说你的做法。OABCD4.如图,在△ABC中,∠BAC=1200,以BC为边向外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.
6.如图,点P是边长为a的正方形ABCD内的一点,连PA、PB、PC,且PB = b ( b
(2)若PB=3,求PP′的长。
(3)在(2)的条件下,若PA=4,
∠APB=135 °,求PC的长。
(4)若PA2+PC2=2PB2,
请说明点P必在对角线AC上。7.如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示)
(图1) (图2) (图3) (图4)
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;解:(1)图形平移的距离就是线段BC的长,
又∵在Rt△ABC中,斜边长为10cm,∠BAC=300,∴BC=5cm,
∴平移的距离为5cm。(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;(图3)(图5)(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH﹦DH(图3)(图5)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
