苏科版数学七上6.1 线段 射线 直线复习课件(25张)
文档属性
| 名称 | 苏科版数学七上6.1 线段 射线 直线复习课件(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
线段、射线、直线(复习课)
线段
射线
直线
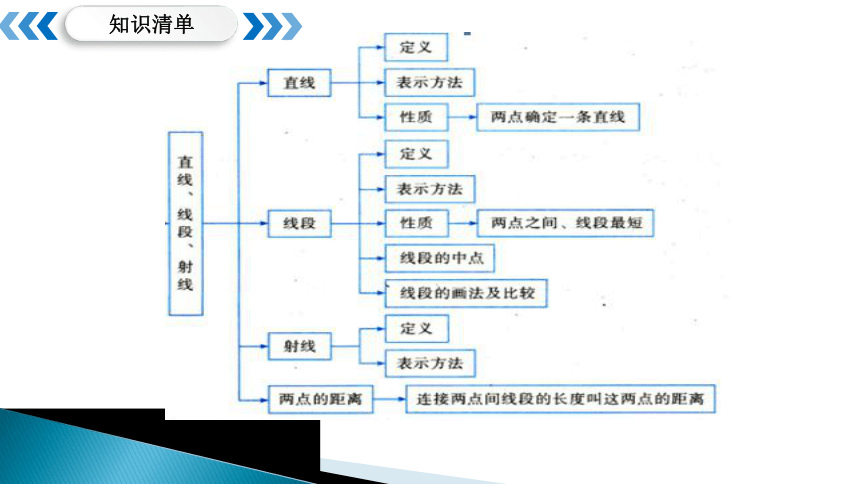
知识清单
名
称 图形 区别 联系
线
段
射
线
直
线
不能延伸
只能向
一方延伸
可向
两方延伸
B
A
A
B
B
A
2
1
0
线段向一方延长就形成射线;
向两方延长就形成直线.
(线段和射线都是直线的一部分,线段也是射线的一部分. )
延伸性
端点数
度量性
可度量
不可度量
不可度量
1、线段、射线、直线的区别与联系
线段
A
B
线段
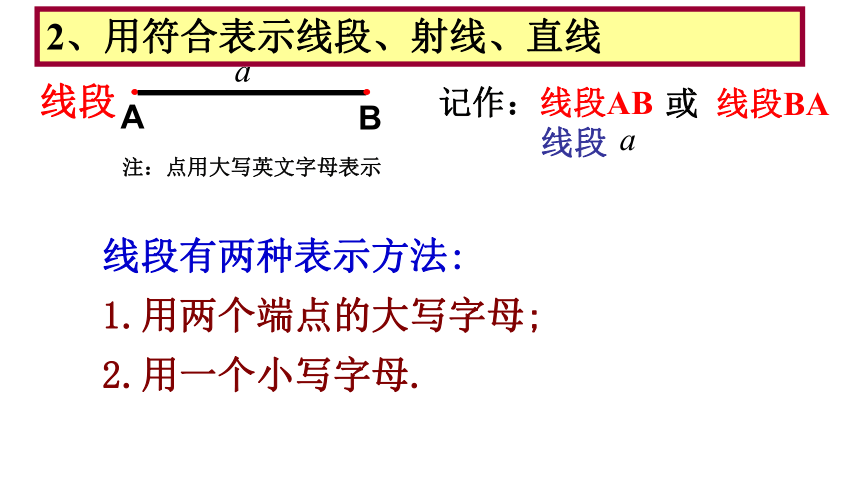
2、用符合表示线段、射线、直线
记作:线段AB
或 线段BA
注:点用大写英文字母表示
线段有两种表示方法:
1.用两个端点的大写字母;
2.用一个小写字母.
(1)它们都能用 个 字母表示;
表示 与 的两个大写字母能交换顺序,
而射线的 字母必须写在前面。
线段
射线
直线
A
B
线段
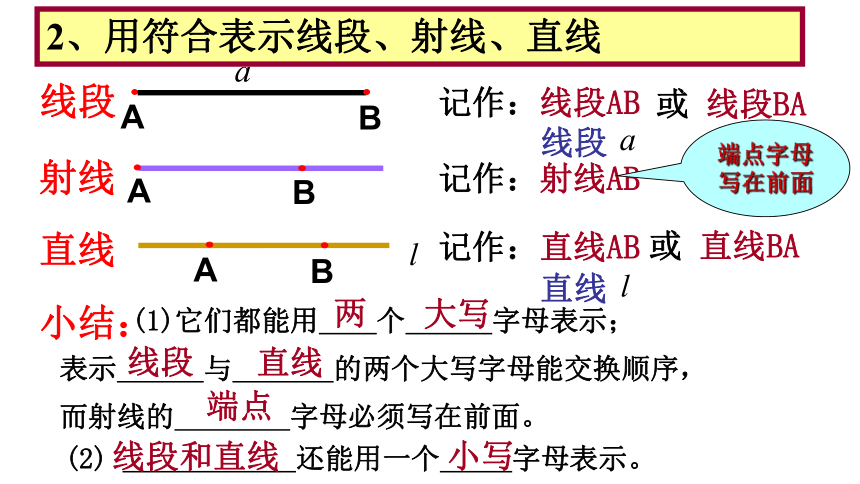
2、用符合表示线段、射线、直线
A
B
A
B
记作:线段AB
或 线段BA
记作:射线AB
记作:直线AB
或 直线BA
直线
两
大写
(2) 还能用一个 字母表示。
线段和直线
小写
端点
端点字母写在前面
线段
直线
小结:
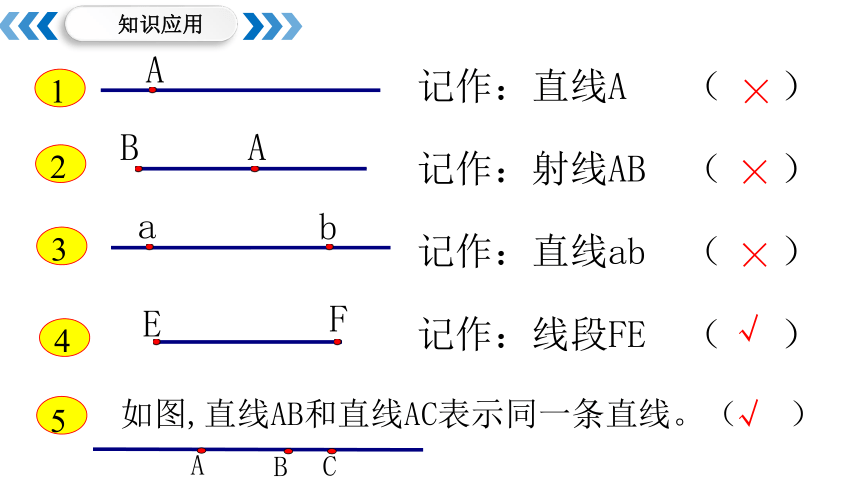
记作:直线A ( )
记作:射线AB ( )
记作:直线ab ( )
记作:线段FE ( )
1
A
A
B
2
a
b
3
E
F
4
5
如图,直线AB和直线AC表示同一条直线。( )
C
A
B
×
×
×
√
√
知识应用
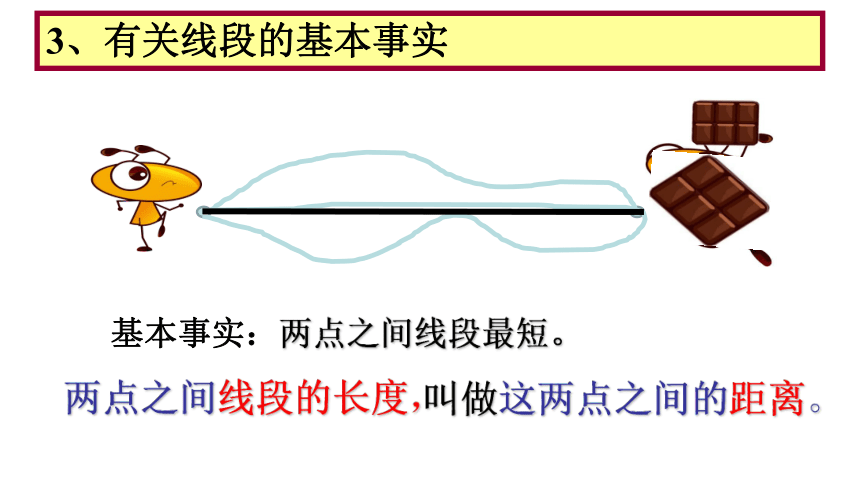
3、有关线段的基本事实
基本事实:两点之间线段最短。
线段的长度,
叫做这两点之间的距离。
两点之间
(2)两点之间的线段叫做两点之间的距离。( )
(1)两点之间所有的连线中,直线最短。 ( )
×
×
(3)从起点到终点,平均速度为40千米/时,半小时后到达;则两点间的距离是20千米。 ( )
×
路程
距离
知识应用
4、有关直线的基本事实
如图,已知点A、B.
A
B
·
·
(2)过A、B两点可以画几条直线?
(1)过点A可以画几条直线?
过一点可以画无数条直线.
基本事实:两点确定一条直线.
…
4、有关直线的基本事实
(3)经过平面内三点中的两点,
你能画出几条直线?
A
B
C
A
B
C
在平面内有A、B、C、D四点,过其中任意两点画一条直线,最多可以画几条?如果有四点呢?五点呢?有何规律?
知识应用
平面内的点数 图中直线条数
2个
3个
4个
5个
n个
1
3
6
10
教室里有2位同学,如果每位同学都要和其他的每一个人握一次手
那么这2个同学一共握手 次,
若是3位同学,一共握手 次,
若是4位同学,一共握手 次,
若是5位同学,一共握手 次,
若是n位同学,一共握手 次。
1
6
10
3
车票、送贺卡类问题
知识应用
①用卷尺分别度量出两个同学的身高,将所得的
数值进行比较。
②让两个同学站在同一平地上,脚底平齐,观看两
人的头顶,直接比出高矮。
5、线段的画法和比较
比较两个同学高矮的方法:
——叠合法
——度量法
思考 :怎样比较两支铅笔的长短?
怎样比较两个同学的高矮?
5、线段的画法和比较
A
B
C
D
比较线段AB、CD的长短
(1) 度量法
用刻度尺量出线段AB=2.5cm,线段CD长4cm,所以线段AB比线段CD短。(记作AB<CD 或 CD >AB)
(2) 叠合法
将一线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上。
记作AB<CD 或 CD >AB
A
M
B
6、线段的中点
定义:将一条线段分成两条相等线段的点,
叫做这条线段的中点.
譬如:如图,AM=BM, 则点M为线段AB的中点
几何格式:
∵点M为AB的中点
∴AM=BM= AB 或者 AB=2AM=2BM
A
B
C
如果B点在线段AC上,
∵ AB=BC(或AB= AC,或BC= AC)
∴点B是线段AC的中点。
∵ 点B是线段AC的中点,
∴ AB=BC= AC
反之
6、线段的中点
2、如图,下列说法不能判断点C是线段AB的中点的是( )
A、AC=CB
B、AB=2AC
C、AC+CB=AB
D、CB= AB
1、如图,AD=AB- =AC+ 。
知识应用
BD
CD
C
典型例题
例1 如图,延长线段AB到点C,使BC=2AB,D是AB的中点,点E、F在BC上,且BE:EF:FC=1:2:5,AC=36.求DE和DF的长.
解:设BE=x,EF=2x,FC=5x,
∴BC=BE+EF+FC=8x,
∵BC=2AB,∴AB=4x,
∵D为AB中点,∴DB=2x,
AC=AB+BC=12x=36,∴x=3.
∴DF=DB+BE+EF=5x=15.
DE=DB+BE=3x=9.
分析:比例线段求值,设x
典型例题
例2 已知线段AB=6,点C是线段AB的中点,点D在直线AB上,且AD=AB,求线段CD的长.
分析:多解问题
本题中,点C的位置是确定的,但点D的位置不确定,它在直线AB上,可能在线段AB上,也可能在延长线上,因此,可以有2解.
解:
典型例题
例3 已知线段AB=8,点M为直线AB上除AB外任意一点,点C是AM的中点,点D是BM的中点,求线段CD的长.
分析:典型的双中点问题
点M的位置不确定,可以在线段AB上,也可以在线段AB的延长线上,也可以在线段BA的延长线上,但是,无论怎样,答案都是定值!
线段CD的长,必然为CM和DM的和或差.
解:
典型例题
例4 如图,在原点为O的数轴上有A、B、C、D四个点,且AB=2, CD=4.已知点A表示的数是-10,点C表示的数是16,若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.
(1)经过多少秒,BC =8?
(2)当BC = 8时,点B表示的数是多少?
解:(1)由题意得,点B表示的数是-8,点C表示的数是16
设经过t秒,BC =8.
①当点B在点C的左边时,有6t+8+2t=16-(-8),所以t=2;
②当点B在点C的右边时,有6t -8+2t=16-(-8),所以t=4.
综上所述,经过2秒或4秒,BC =8
(2)当BC = 8时,由(1)可知线段AB向右匀速运动2秒或4秒,即点B向右匀速运动12个单位长度或24个单位长度.
所以点B表示的数是4或16.
分析:动态问题
归纳小结
发挥你的想象,课后尝试你的创作。
神奇的线段
?
?
?
?
谢
谢
再
见
线段、射线、直线(复习课)
线段
射线
直线
知识清单
名
称 图形 区别 联系
线
段
射
线
直
线
不能延伸
只能向
一方延伸
可向
两方延伸
B
A
A
B
B
A
2
1
0
线段向一方延长就形成射线;
向两方延长就形成直线.
(线段和射线都是直线的一部分,线段也是射线的一部分. )
延伸性
端点数
度量性
可度量
不可度量
不可度量
1、线段、射线、直线的区别与联系
线段
A
B
线段
2、用符合表示线段、射线、直线
记作:线段AB
或 线段BA
注:点用大写英文字母表示
线段有两种表示方法:
1.用两个端点的大写字母;
2.用一个小写字母.
(1)它们都能用 个 字母表示;
表示 与 的两个大写字母能交换顺序,
而射线的 字母必须写在前面。
线段
射线
直线
A
B
线段
2、用符合表示线段、射线、直线
A
B
A
B
记作:线段AB
或 线段BA
记作:射线AB
记作:直线AB
或 直线BA
直线
两
大写
(2) 还能用一个 字母表示。
线段和直线
小写
端点
端点字母写在前面
线段
直线
小结:
记作:直线A ( )
记作:射线AB ( )
记作:直线ab ( )
记作:线段FE ( )
1
A
A
B
2
a
b
3
E
F
4
5
如图,直线AB和直线AC表示同一条直线。( )
C
A
B
×
×
×
√
√
知识应用
3、有关线段的基本事实
基本事实:两点之间线段最短。
线段的长度,
叫做这两点之间的距离。
两点之间
(2)两点之间的线段叫做两点之间的距离。( )
(1)两点之间所有的连线中,直线最短。 ( )
×
×
(3)从起点到终点,平均速度为40千米/时,半小时后到达;则两点间的距离是20千米。 ( )
×
路程
距离
知识应用
4、有关直线的基本事实
如图,已知点A、B.
A
B
·
·
(2)过A、B两点可以画几条直线?
(1)过点A可以画几条直线?
过一点可以画无数条直线.
基本事实:两点确定一条直线.
…
4、有关直线的基本事实
(3)经过平面内三点中的两点,
你能画出几条直线?
A
B
C
A
B
C
在平面内有A、B、C、D四点,过其中任意两点画一条直线,最多可以画几条?如果有四点呢?五点呢?有何规律?
知识应用
平面内的点数 图中直线条数
2个
3个
4个
5个
n个
1
3
6
10
教室里有2位同学,如果每位同学都要和其他的每一个人握一次手
那么这2个同学一共握手 次,
若是3位同学,一共握手 次,
若是4位同学,一共握手 次,
若是5位同学,一共握手 次,
若是n位同学,一共握手 次。
1
6
10
3
车票、送贺卡类问题
知识应用
①用卷尺分别度量出两个同学的身高,将所得的
数值进行比较。
②让两个同学站在同一平地上,脚底平齐,观看两
人的头顶,直接比出高矮。
5、线段的画法和比较
比较两个同学高矮的方法:
——叠合法
——度量法
思考 :怎样比较两支铅笔的长短?
怎样比较两个同学的高矮?
5、线段的画法和比较
A
B
C
D
比较线段AB、CD的长短
(1) 度量法
用刻度尺量出线段AB=2.5cm,线段CD长4cm,所以线段AB比线段CD短。(记作AB<CD 或 CD >AB)
(2) 叠合法
将一线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上。
记作AB<CD 或 CD >AB
A
M
B
6、线段的中点
定义:将一条线段分成两条相等线段的点,
叫做这条线段的中点.
譬如:如图,AM=BM, 则点M为线段AB的中点
几何格式:
∵点M为AB的中点
∴AM=BM= AB 或者 AB=2AM=2BM
A
B
C
如果B点在线段AC上,
∵ AB=BC(或AB= AC,或BC= AC)
∴点B是线段AC的中点。
∵ 点B是线段AC的中点,
∴ AB=BC= AC
反之
6、线段的中点
2、如图,下列说法不能判断点C是线段AB的中点的是( )
A、AC=CB
B、AB=2AC
C、AC+CB=AB
D、CB= AB
1、如图,AD=AB- =AC+ 。
知识应用
BD
CD
C
典型例题
例1 如图,延长线段AB到点C,使BC=2AB,D是AB的中点,点E、F在BC上,且BE:EF:FC=1:2:5,AC=36.求DE和DF的长.
解:设BE=x,EF=2x,FC=5x,
∴BC=BE+EF+FC=8x,
∵BC=2AB,∴AB=4x,
∵D为AB中点,∴DB=2x,
AC=AB+BC=12x=36,∴x=3.
∴DF=DB+BE+EF=5x=15.
DE=DB+BE=3x=9.
分析:比例线段求值,设x
典型例题
例2 已知线段AB=6,点C是线段AB的中点,点D在直线AB上,且AD=AB,求线段CD的长.
分析:多解问题
本题中,点C的位置是确定的,但点D的位置不确定,它在直线AB上,可能在线段AB上,也可能在延长线上,因此,可以有2解.
解:
典型例题
例3 已知线段AB=8,点M为直线AB上除AB外任意一点,点C是AM的中点,点D是BM的中点,求线段CD的长.
分析:典型的双中点问题
点M的位置不确定,可以在线段AB上,也可以在线段AB的延长线上,也可以在线段BA的延长线上,但是,无论怎样,答案都是定值!
线段CD的长,必然为CM和DM的和或差.
解:
典型例题
例4 如图,在原点为O的数轴上有A、B、C、D四个点,且AB=2, CD=4.已知点A表示的数是-10,点C表示的数是16,若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.
(1)经过多少秒,BC =8?
(2)当BC = 8时,点B表示的数是多少?
解:(1)由题意得,点B表示的数是-8,点C表示的数是16
设经过t秒,BC =8.
①当点B在点C的左边时,有6t+8+2t=16-(-8),所以t=2;
②当点B在点C的右边时,有6t -8+2t=16-(-8),所以t=4.
综上所述,经过2秒或4秒,BC =8
(2)当BC = 8时,由(1)可知线段AB向右匀速运动2秒或4秒,即点B向右匀速运动12个单位长度或24个单位长度.
所以点B表示的数是4或16.
分析:动态问题
归纳小结
发挥你的想象,课后尝试你的创作。
神奇的线段
?
?
?
?
谢
谢
再
见
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
