苏科版数学七上6.3 余角 补角 对顶角 复习课件(24张)
文档属性
| 名称 | 苏科版数学七上6.3 余角 补角 对顶角 复习课件(24张) |  | |
| 格式 | zip | ||
| 文件大小 | 486.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 13:47:36 | ||
图片预览



文档简介
(共24张PPT)
余角、补角、对顶角(复习课)
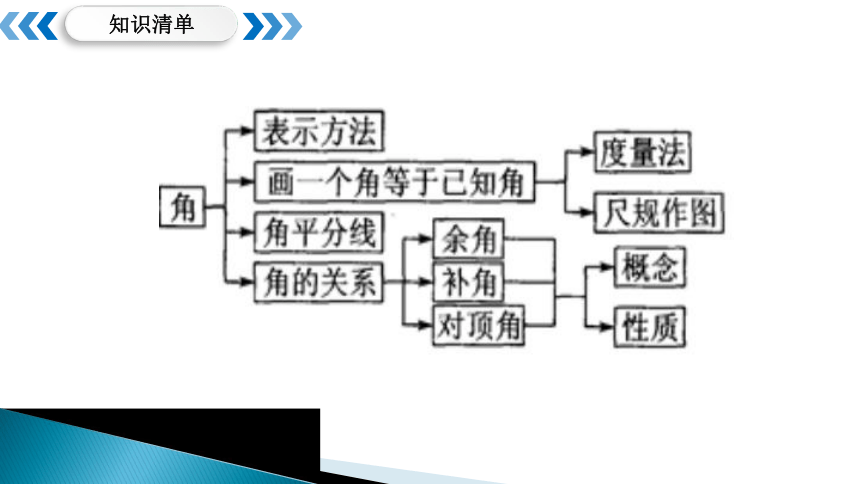
知识清单
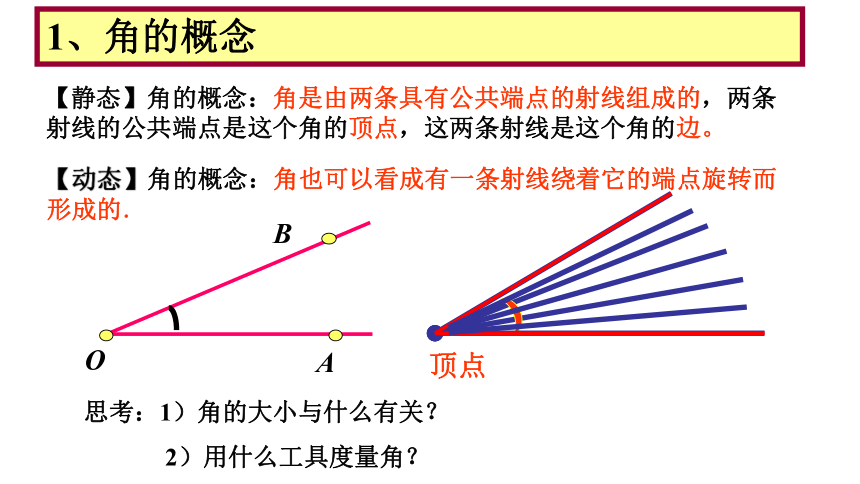
1、角的概念
【静态】角的概念:角是由两条具有公共端点的射线组成的,两条射线的公共端点是这个角的顶点,这两条射线是这个角的边。
【动态】角的概念:角也可以看成有一条射线绕着它的端点旋转而形成的.
B
O
A
顶点
思考:1)角的大小与什么有关?
2)用什么工具度量角?
2、角的表示方法
(1)用三个字母表示角时,表示顶点的字母必须写在另两个字母的中间.如∠AOB或∠BOA;
B
O
A
(2)在不引起混淆的情况下,角还可以用它的顶点字母来表示.如∠A;
A
(3)角可以用希腊字母来表示,一般地,用希腊字母表示一个角时,需在角内靠近顶点处画上弧线.如∠α;
α
1
(4)角可以用一个数字来表示,一般地,用一个数字表示一个角时,需在角内靠近顶点处画上弧线.如∠1.
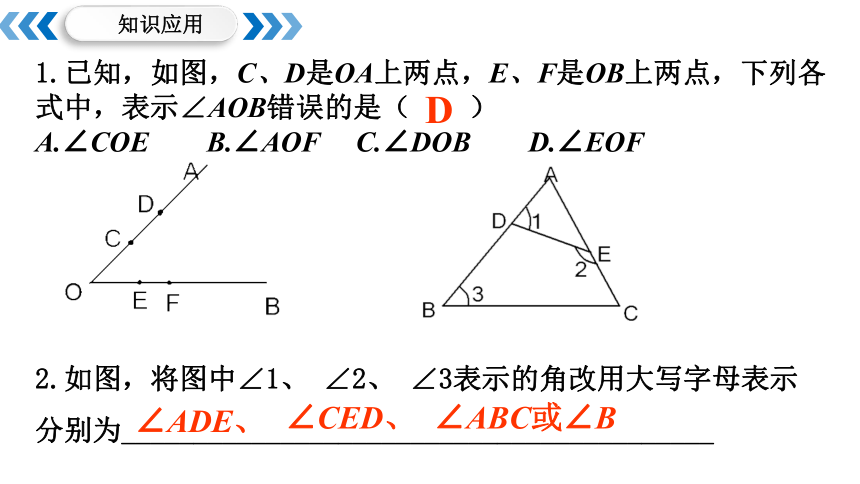
知识应用
1.已知,如图,C、D是OA上两点,E、F是OB上两点,下列各式中,表示∠AOB错误的是( )
A.∠COE B.∠AOF C.∠DOB D.∠EOF
D
2.如图,将图中∠1、 ∠2、 ∠3表示的角改用大写字母表示分别为_________________________________________
∠ADE、
∠CED、
∠ABC或∠B
3、角的画法和比较
思考 :怎样比较角的大小?
度量法或叠合法
用量角器量角,度、分、秒是常用的角的度量单位。
度分秒关系:1°=60′ 1′=60″
如图,以OA为一边的角有哪几个?用“<”号连接起来。
O
A
B
C
D
∠AOD
∠AOC
∠AOB
﹤
﹤
注:找到公共边
练习(1)2.8°= ° ′;
(2)39°36′= °
2
48
39.6
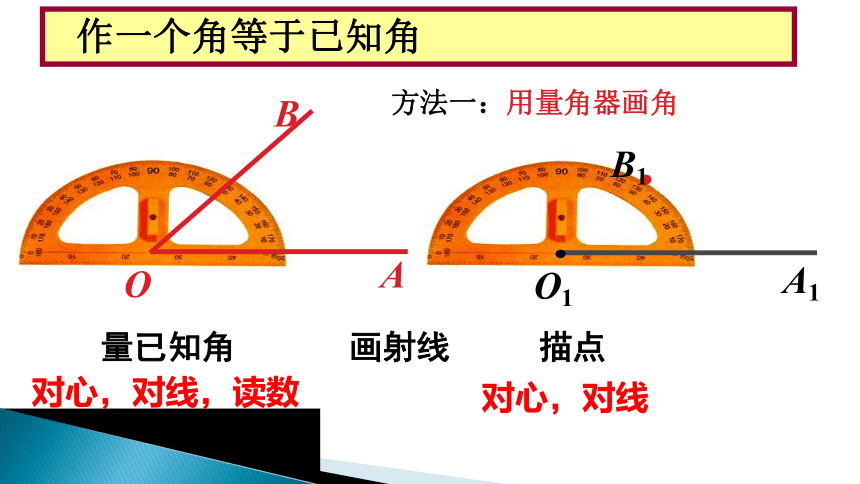
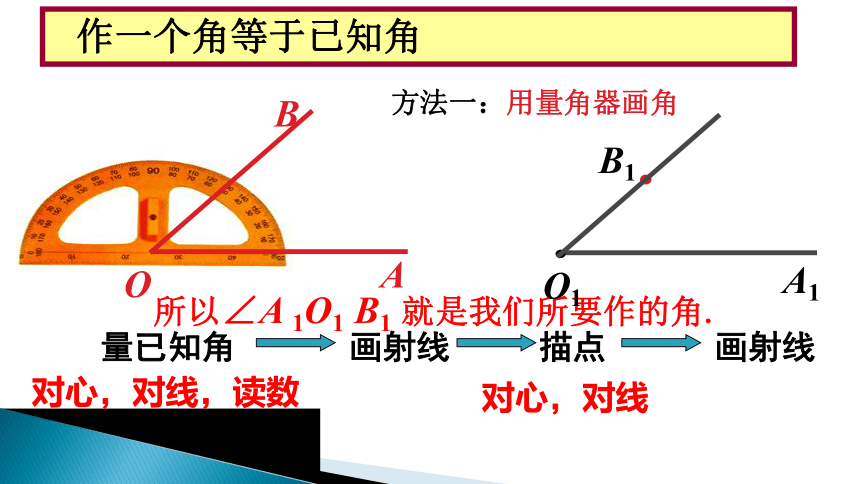
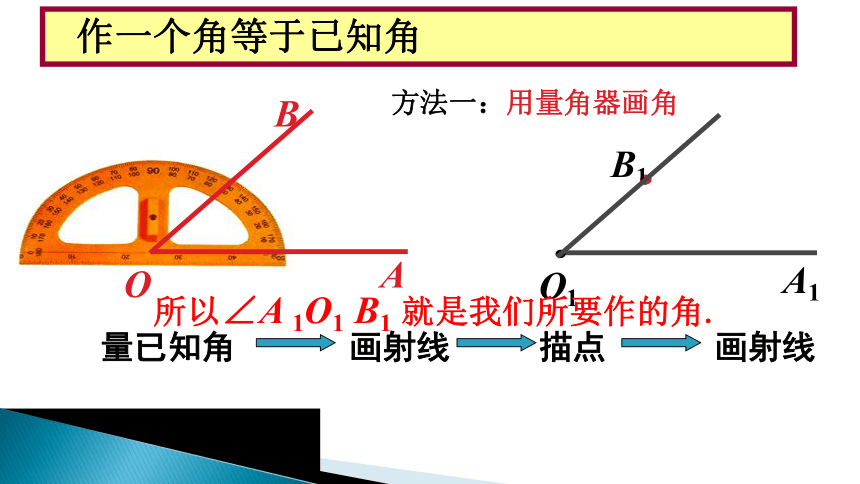
方法一:用量角器画角
O
A
B
A1
O1
量已知角
画射线
描点
B1
对心,对线,读数
对心,对线
作一个角等于已知角
所以∠A 1O1 B1 就是我们所要作的角.
O
A
B
A1
O1
量已知角
画射线
描点
B1
画射线
对心,对线,读数
对心,对线
方法一:用量角器画角
作一个角等于已知角
O
A
B
A1
O1
量已知角
画射线
描点
B1
画射线
方法一:用量角器画角
作一个角等于已知角
所以∠A 1O1 B1 就是我们所要作的角.
用尺规画角的步骤:
● 以O为圆心,以适当长为半径画弧,交角的两边于C, D两点;
● 画射线EF,以E为圆心,以同样长为半径画弧,交射线EF于G点;
● 以C为圆心,以线段CD长为半径画弧,;
● 画射线EH.
O
A
B
C
D
G
E
F
● 再以点G为圆心,以同样长为半径画弧,交原先的弧交于点H;
H
方法二:用尺规画角
作一个角等于已知角
4、角的平分线
定义:如图,OC将∠AOB分成相等的两部分,
OC叫做∠AOB的角平分线.
几何格式:
O
B
C
A
5、余角、补角
互为余角的概念:
如果两个角的和是一个直角,
这两个角叫做互为余角.简称互余.
其中一个角叫做另一个角的余角.
互为补角的概念:
如果两个角的和是一个平角,
这两个角叫做互为补角.简称互补.
其中一个角叫做另一个角的补角.
1
2
A
B
C
o
1
2
A
B
C
o
互余、互补是两个角的数量关系,而非位置关系.
知识应用
如图,A、O、B在一条直线上,∠AOC, ∠DOE是直角
①写出所有与∠BOD互余的角_____________
②写出所有与∠BOD互补的角_____________
×
×
∠BOE, ∠COD
∠AOD, ∠COE
余角性质:同角(或等角)的余角相等。
补角性质:同角(或等角)的补角相等。
6、对顶角
4
3
2
1
A
B
C
D
对顶角的性质:对顶角相等
定义:一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对顶角。
知识应用
下列各图中,哪些组中∠l和∠2是对顶角?
典型例题
例1 已知一个角的补角比这个角的余角的3倍小20°,求这个角的度数.
分析:设未知数,建立方程
解:设这个角为x度
根据题意得
180 - x = 3(90 - x)- 20
解得 x=35
答:这个角为35°。
典型例题
例2 如图,直线AB、CD相交于点O,已知∠AOC=50°,OE把∠BOD分成两部分,∠BOE:∠EOD=2:3.求∠EOD的度数.
解: ∵ ∠BOE:∠EOD=2:3
∴设∠BOE =2x,∠EOD=3x
∴ ∠BOD = ∠BOE+∠EOD=5x
∵∠AOC与∠BOD是对顶角
∴∠AOC=∠BOD=5x=50°
∴ x=10°
∴ ∠EOD=3x =30°
分析:比值问题,设x
O
A
B
C
D
E
典型例题
例3 已知∠AOC=60°,∠BOC=40°,求∠AOB的度数.
分析:多解问题
解:
O
B
C
A
C
B
A
O
∠AOB =∠AOC+∠BOC=100 °
∠AOB =∠AOC-∠BOC=20 °
典型例题
变式 已知∠AOC=60°, ∠BOC=40°, OM、ON分别是∠AOC、∠BOC的角平分线,求∠MON的度数。
解:
C
N
O
A
B
M
O
A
B
M
C
N
∵ OM、ON分别是∠AOC、
∠BOC的角平分线
∴∠MOC=∠AOC=30 °
∠NOC=∠BOC=20 °
∴∠MON =∠MOC+∠NOC=50 °
或∠MON =∠MOC-∠NOC=10 °
O
B
C
A
C
B
A
O
典型例题
变式 已知OM、ON分别是∠AOC、∠BOC的角平分线,若∠AOB=100°,求∠MON的度数。
解:
C
N
O
A
B
M
∵ OM、ON分别是∠AOC、
∠BOC的角平分线
∴∠MOC=∠AOC
∠NOC=∠BOC
∴∠MON =∠MOC+∠NOC
=∠AOC + ∠BOC
= ∠AOB
=50 °
问:若∠MON=60°,则∠AOB = _____
综上所述: ∠MON=_____∠AOB.
120°
典型例题
例4 如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上, 另一边ON在直线AB的下方.将图1中的三角板绕点O以每秒2°的速度逆时针旋转至图2 ,使一边OM在∠BOC的内部,设运动时间为t秒.
(1)若OM恰好平分∠BOC,求t的值;
分析:动态问题
解: (1) ∵ ∠AOC=60°∴ ∠BOC=120°
∵ OM平分∠BOC
∴ ∠BOM=∠BOC=60°
∴2 t =60°即t =30°
典型例题
(2)若∠BOM等于∠COM余角的
3倍, 求∠BON的度数;
(3)当t为何值时,∠BON= 30°.
(3) 有两种情况
①如图2 ∵ ∠BON= 30°
∴ ∠BOM= 2 t =60° ∴ t =30
②如图3 ∵ ∠BON= 30°
∴ ∠BOM= 2 t =120° ∴ t =60
此时∠BOM = ∠BOC , OM不在∠BOC的内部,舍去
答:当t=30时,∠BON= 30°.
(2) ∵ ∠BOM=2 t
∴ ∠COM= 9 0° × 2 t
由题意得 :
2 t + 9 0° × 2 t=120°
解得: t =22.5°∴ ∠BOM =45°
∵ ∠MON=90° ∴ ∠BON =45°
N
M
图3
将三角板绕点O以每秒2°的速度逆时针旋转一周,当t为何值时,可使射线OA,OC与OM中的某一条射线是另两条射线所夹角的角平分线?
归纳小结
?
?
?
?
谢
谢
再
见
余角、补角、对顶角(复习课)
知识清单
1、角的概念
【静态】角的概念:角是由两条具有公共端点的射线组成的,两条射线的公共端点是这个角的顶点,这两条射线是这个角的边。
【动态】角的概念:角也可以看成有一条射线绕着它的端点旋转而形成的.
B
O
A
顶点
思考:1)角的大小与什么有关?
2)用什么工具度量角?
2、角的表示方法
(1)用三个字母表示角时,表示顶点的字母必须写在另两个字母的中间.如∠AOB或∠BOA;
B
O
A
(2)在不引起混淆的情况下,角还可以用它的顶点字母来表示.如∠A;
A
(3)角可以用希腊字母来表示,一般地,用希腊字母表示一个角时,需在角内靠近顶点处画上弧线.如∠α;
α
1
(4)角可以用一个数字来表示,一般地,用一个数字表示一个角时,需在角内靠近顶点处画上弧线.如∠1.
知识应用
1.已知,如图,C、D是OA上两点,E、F是OB上两点,下列各式中,表示∠AOB错误的是( )
A.∠COE B.∠AOF C.∠DOB D.∠EOF
D
2.如图,将图中∠1、 ∠2、 ∠3表示的角改用大写字母表示分别为_________________________________________
∠ADE、
∠CED、
∠ABC或∠B
3、角的画法和比较
思考 :怎样比较角的大小?
度量法或叠合法
用量角器量角,度、分、秒是常用的角的度量单位。
度分秒关系:1°=60′ 1′=60″
如图,以OA为一边的角有哪几个?用“<”号连接起来。
O
A
B
C
D
∠AOD
∠AOC
∠AOB
﹤
﹤
注:找到公共边
练习(1)2.8°= ° ′;
(2)39°36′= °
2
48
39.6
方法一:用量角器画角
O
A
B
A1
O1
量已知角
画射线
描点
B1
对心,对线,读数
对心,对线
作一个角等于已知角
所以∠A 1O1 B1 就是我们所要作的角.
O
A
B
A1
O1
量已知角
画射线
描点
B1
画射线
对心,对线,读数
对心,对线
方法一:用量角器画角
作一个角等于已知角
O
A
B
A1
O1
量已知角
画射线
描点
B1
画射线
方法一:用量角器画角
作一个角等于已知角
所以∠A 1O1 B1 就是我们所要作的角.
用尺规画角的步骤:
● 以O为圆心,以适当长为半径画弧,交角的两边于C, D两点;
● 画射线EF,以E为圆心,以同样长为半径画弧,交射线EF于G点;
● 以C为圆心,以线段CD长为半径画弧,;
● 画射线EH.
O
A
B
C
D
G
E
F
● 再以点G为圆心,以同样长为半径画弧,交原先的弧交于点H;
H
方法二:用尺规画角
作一个角等于已知角
4、角的平分线
定义:如图,OC将∠AOB分成相等的两部分,
OC叫做∠AOB的角平分线.
几何格式:
O
B
C
A
5、余角、补角
互为余角的概念:
如果两个角的和是一个直角,
这两个角叫做互为余角.简称互余.
其中一个角叫做另一个角的余角.
互为补角的概念:
如果两个角的和是一个平角,
这两个角叫做互为补角.简称互补.
其中一个角叫做另一个角的补角.
1
2
A
B
C
o
1
2
A
B
C
o
互余、互补是两个角的数量关系,而非位置关系.
知识应用
如图,A、O、B在一条直线上,∠AOC, ∠DOE是直角
①写出所有与∠BOD互余的角_____________
②写出所有与∠BOD互补的角_____________
×
×
∠BOE, ∠COD
∠AOD, ∠COE
余角性质:同角(或等角)的余角相等。
补角性质:同角(或等角)的补角相等。
6、对顶角
4
3
2
1
A
B
C
D
对顶角的性质:对顶角相等
定义:一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对顶角。
知识应用
下列各图中,哪些组中∠l和∠2是对顶角?
典型例题
例1 已知一个角的补角比这个角的余角的3倍小20°,求这个角的度数.
分析:设未知数,建立方程
解:设这个角为x度
根据题意得
180 - x = 3(90 - x)- 20
解得 x=35
答:这个角为35°。
典型例题
例2 如图,直线AB、CD相交于点O,已知∠AOC=50°,OE把∠BOD分成两部分,∠BOE:∠EOD=2:3.求∠EOD的度数.
解: ∵ ∠BOE:∠EOD=2:3
∴设∠BOE =2x,∠EOD=3x
∴ ∠BOD = ∠BOE+∠EOD=5x
∵∠AOC与∠BOD是对顶角
∴∠AOC=∠BOD=5x=50°
∴ x=10°
∴ ∠EOD=3x =30°
分析:比值问题,设x
O
A
B
C
D
E
典型例题
例3 已知∠AOC=60°,∠BOC=40°,求∠AOB的度数.
分析:多解问题
解:
O
B
C
A
C
B
A
O
∠AOB =∠AOC+∠BOC=100 °
∠AOB =∠AOC-∠BOC=20 °
典型例题
变式 已知∠AOC=60°, ∠BOC=40°, OM、ON分别是∠AOC、∠BOC的角平分线,求∠MON的度数。
解:
C
N
O
A
B
M
O
A
B
M
C
N
∵ OM、ON分别是∠AOC、
∠BOC的角平分线
∴∠MOC=∠AOC=30 °
∠NOC=∠BOC=20 °
∴∠MON =∠MOC+∠NOC=50 °
或∠MON =∠MOC-∠NOC=10 °
O
B
C
A
C
B
A
O
典型例题
变式 已知OM、ON分别是∠AOC、∠BOC的角平分线,若∠AOB=100°,求∠MON的度数。
解:
C
N
O
A
B
M
∵ OM、ON分别是∠AOC、
∠BOC的角平分线
∴∠MOC=∠AOC
∠NOC=∠BOC
∴∠MON =∠MOC+∠NOC
=∠AOC + ∠BOC
= ∠AOB
=50 °
问:若∠MON=60°,则∠AOB = _____
综上所述: ∠MON=_____∠AOB.
120°
典型例题
例4 如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上, 另一边ON在直线AB的下方.将图1中的三角板绕点O以每秒2°的速度逆时针旋转至图2 ,使一边OM在∠BOC的内部,设运动时间为t秒.
(1)若OM恰好平分∠BOC,求t的值;
分析:动态问题
解: (1) ∵ ∠AOC=60°∴ ∠BOC=120°
∵ OM平分∠BOC
∴ ∠BOM=∠BOC=60°
∴2 t =60°即t =30°
典型例题
(2)若∠BOM等于∠COM余角的
3倍, 求∠BON的度数;
(3)当t为何值时,∠BON= 30°.
(3) 有两种情况
①如图2 ∵ ∠BON= 30°
∴ ∠BOM= 2 t =60° ∴ t =30
②如图3 ∵ ∠BON= 30°
∴ ∠BOM= 2 t =120° ∴ t =60
此时∠BOM = ∠BOC , OM不在∠BOC的内部,舍去
答:当t=30时,∠BON= 30°.
(2) ∵ ∠BOM=2 t
∴ ∠COM= 9 0° × 2 t
由题意得 :
2 t + 9 0° × 2 t=120°
解得: t =22.5°∴ ∠BOM =45°
∵ ∠MON=90° ∴ ∠BON =45°
N
M
图3
将三角板绕点O以每秒2°的速度逆时针旋转一周,当t为何值时,可使射线OA,OC与OM中的某一条射线是另两条射线所夹角的角平分线?
归纳小结
?
?
?
?
谢
谢
再
见
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
