苏科版数学七上6.4 平行与垂直 复习课件(24张)
文档属性
| 名称 | 苏科版数学七上6.4 平行与垂直 复习课件(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 597.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
平行与垂直(复习课)
知识清单
两条直线的位置关系
平行
相交
垂直
概念、画法、性质
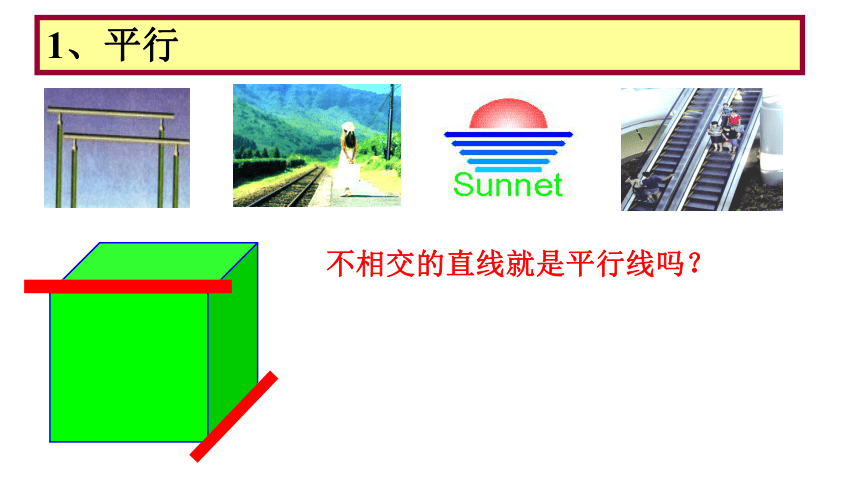
1、平行
不相交的直线就是平行线吗?
1、平行
定义:在同一平面内不相交的两条直线叫做平行线。
“平行”用符号“∥”表示.
如图 ,直线AB平行于直线CD,
记作AB ∥ CD.
或直线m平行于直线n ,记作:m∥n
A
B
C
D
m
n
①平行线的定义及表示方法
1、平行
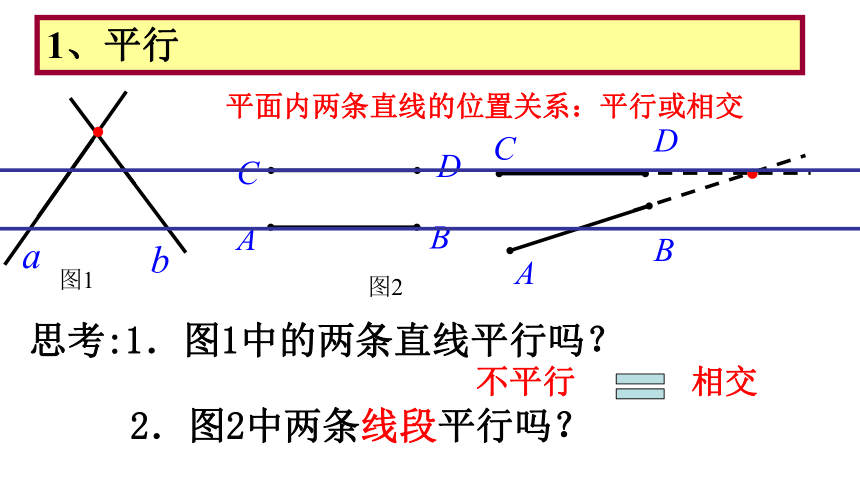
思考:1.图1中的两条直线平行吗?
a
b
图1
2.图2中两条线段平行吗?
A
B
C
D
A
B
C
D
图2
平面内两条直线的位置关系:平行或相交
不平行
相交
1、平行
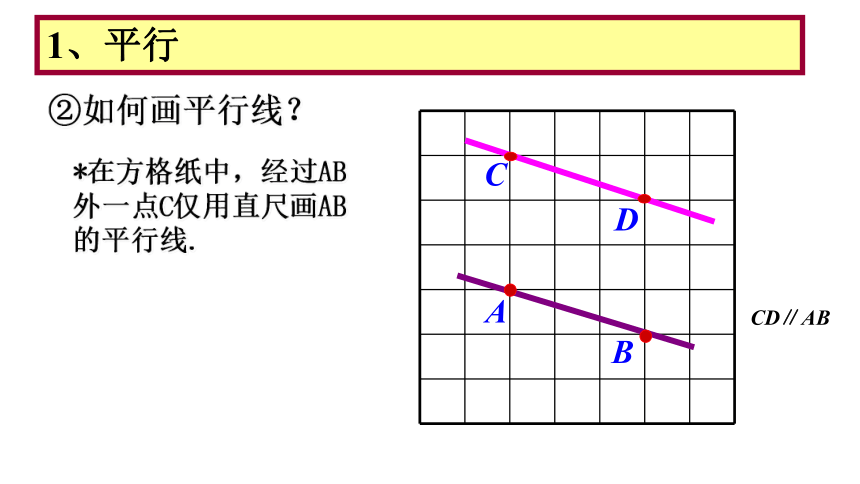
②如何画平行线?
*在方格纸中,经过AB外一点C仅用直尺画AB的平行线.
A
B
C
D
CD∥AB
1、平行
②如何画平行线?
*用直尺和三角尺,经过AB外一点C画AB的平行线.
一放
二靠
四画
三移
*在方格纸中,经过AB外一点C仅用直尺画AB的平行线.
A
B
C
D
CD∥AB
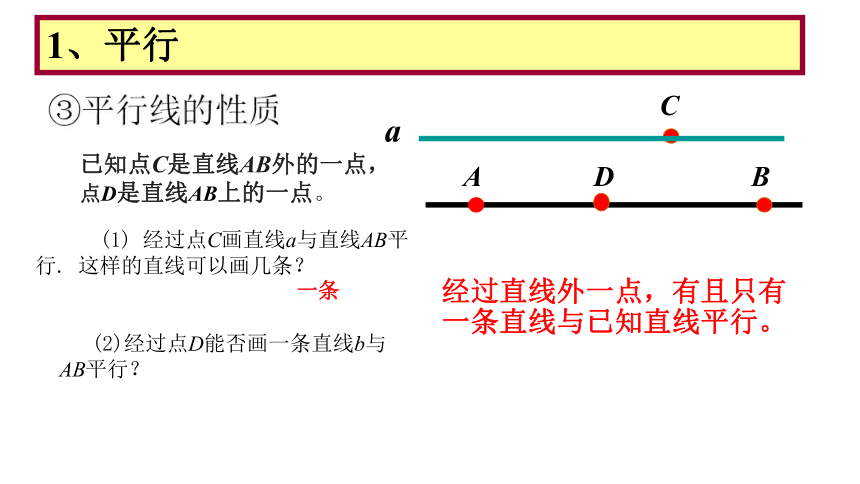
1、平行
③平行线的性质
(1) 经过点C画直线a与直线AB平行. 这样的直线可以画几条?
A
B
C
a
D
(2)经过点D能否画一条直线b与AB平行?
经过直线外一点,有且只有一条直线与已知直线平行。
已知点C是直线AB外的一点,点D是直线AB上的一点。
一条
知识应用
1.如图,已知直线a、b、c在同一个平面内,a∥b,a与c相交于点A,那么b与c一定相交吗?为什么?
因为经过直线b外一点A ,有且只有一条直线a与已知直线b平行,
所以b与c一定相交。
答:相交
2.已知O是直线CD外一点,OA∥CD,OB∥CD,则∠AOB是平角吗?为什么?
O
A
B
C
D
答:是
∵ OA∥CD,OB∥CD
∴OA、OB表示同一条直线
即 点A、O、B在同一条直线上
∴ ∠AOB是平
2、垂直
①垂直的定义及表示方法
定义:如果两条直线相交成直角,那么这两条直线互相垂直。其中一条直线叫做另一条直线的垂线。两条直线的交点叫做垂足。
A
B
C
D
O
“垂直”用符号“⊥”表示.
如图 ,直线AB垂直于直线CD,
记作AB ⊥ CD,垂足为O.
垂直定义的应用:
若直线AB和CD相交,交点为O,∠BOC=90°,则AB⊥CD.这个推理过程可表示为:
∵ ∠BOC=90°
∴ AB⊥CD
2、垂直
①垂直的定义及表示方法
A
B
C
D
O
反之:若两条直线AB⊥CD,垂足为点O,
则∠AOC=∠AOD=∠BOC=∠BOD=90°,
这个推理过程可表示为:
∵ AB⊥CD
∴ ∠BOC=90°
2、垂直
②如何画垂线?(请用三角尺过点P画直线AB的垂线.)
A B
O
P
2、垂直
②如何画垂线?(请用三角尺过点P画直线AB的垂线.)
A
B
P
C
能画几条呢?
一放
二移
三画
2、垂直
③垂线的性质
性质1:过一点有且只有一条直线与已知直线垂直.
性质2 :连接直线外一点与直线上各点的所有线段中,垂线段最短.
简称为“垂线段最短”.
垂线段CF的长度,称为点C 到直线AB 的距离。
C
A
B
F
E
D
G
H
2、垂直
④点到直线的距离
定义:直线外一点到这条直线的垂线段的长度,
叫做点到直线的距离。
C
A
B
F
E
D
G
H
垂线段CF的长度,称为点C 到直线 AB 的距离。
*线段、射线的垂线应怎么画呢?学.科.网
A
B
P
Q
O
A
注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线.
画一条线段或射线的垂线,就是画它们所在直线的垂线
2、垂直
典型例题
例1 如图,污水处理厂要从A处把处理过的水引入排水沟PQ,应如何铺设排水管道,才能使用料最省?试画出铺设管道的路线?并说明理由。
解:从点A向PQ作垂线段AB,垂
足为B,则线段AB就是铺设管
道的路线。
A
Q
P
B
理由:垂线段最短。
例2 如图,P是∠AOB的边OB上一点。
(1)过点P画OB的垂线,交OA于点C;
(2)过点P画OA的垂线,垂足为H。
比较PH与PC、PC与CO的长短,并说明理由。
典型例题
O
P
B
C
H
A
解:PH<PC,PC<CO
理由:垂线段最短。
例3 如图,点O是直线AB上一点,∠AOC=40°,OD平分∠AOC,∠COE=70°.
(1)请你说明DO⊥OE;
(2)OE平分∠BOC吗?为什么?
解(1) ∵OD平分∠AOC
∴ ∠DOC=∠AOC= 20°
∵∠COE=70°
∴∠DOE=90°
∴ DO⊥OE
典型例题
(2)OE平分∠BOC.
∵∠AOC+∠COE+∠BOE=180°
又∵∠AOC=40°,∠COE=70°
∴∠BOE=70°
∴∠BOE=∠COE
∴OE平分∠BOC
例4 一副直角三角板叠放如图①,现将含45°角的三角板ADE 固定不动,把含30°角的三角板ABC绕顶点A顺时针旋转角α(α=∠BAD且0°<α<180°),使两块三角板至少有一组对应边(所在的直线)垂直.
(1)如图②,α= °时,BC⊥AE;
(2)请你在备用图中画一种符合要求的图形,用符号表示出垂直的边,并计算出旋转角α.
典型例题
15
典型例题
使两块三角板至少有一组对应边(所在的直线)垂直.
用符号表示出垂直的边,并计算出旋转角α(∠BAD)
BC⊥AE
α=15°
AC⊥AE
α= °
AC⊥AD
α= °
AB⊥AE
α= °
105
60
135
记作:AB∥CD 读作AB平行于CD
1.在同一平面内不相交的两条直线叫做平行线。
作法:一放、二靠、三移、四画
归纳小结
过直线外一点有且只有一条直线与已知直线平行。
2.过直线外一点做已知直线的平行线
3. 平行线的性质
平行
A
B
C
D
记作:AB⊥CD 读作AB垂直于CD
1.如果两条直线相交成直角,那么这两条直线互相垂直。
其中一条直线叫做另一条直线的垂线。两条直线的交点叫做垂足。
作法:一放、二移、三画
归纳小结
(1)过一点有且只有一条直线与已知直线垂直。
(2)连接直线外一点与直线上各点的所有线段中,垂线段最短。
*这条垂线段的长度叫做点到直线的距离。
2.过一点做已知直线的垂线
3. 垂线的性质
垂直
A
B
C
D
O
?
?
?
?
谢
谢
再
见
平行与垂直(复习课)
知识清单
两条直线的位置关系
平行
相交
垂直
概念、画法、性质
1、平行
不相交的直线就是平行线吗?
1、平行
定义:在同一平面内不相交的两条直线叫做平行线。
“平行”用符号“∥”表示.
如图 ,直线AB平行于直线CD,
记作AB ∥ CD.
或直线m平行于直线n ,记作:m∥n
A
B
C
D
m
n
①平行线的定义及表示方法
1、平行
思考:1.图1中的两条直线平行吗?
a
b
图1
2.图2中两条线段平行吗?
A
B
C
D
A
B
C
D
图2
平面内两条直线的位置关系:平行或相交
不平行
相交
1、平行
②如何画平行线?
*在方格纸中,经过AB外一点C仅用直尺画AB的平行线.
A
B
C
D
CD∥AB
1、平行
②如何画平行线?
*用直尺和三角尺,经过AB外一点C画AB的平行线.
一放
二靠
四画
三移
*在方格纸中,经过AB外一点C仅用直尺画AB的平行线.
A
B
C
D
CD∥AB
1、平行
③平行线的性质
(1) 经过点C画直线a与直线AB平行. 这样的直线可以画几条?
A
B
C
a
D
(2)经过点D能否画一条直线b与AB平行?
经过直线外一点,有且只有一条直线与已知直线平行。
已知点C是直线AB外的一点,点D是直线AB上的一点。
一条
知识应用
1.如图,已知直线a、b、c在同一个平面内,a∥b,a与c相交于点A,那么b与c一定相交吗?为什么?
因为经过直线b外一点A ,有且只有一条直线a与已知直线b平行,
所以b与c一定相交。
答:相交
2.已知O是直线CD外一点,OA∥CD,OB∥CD,则∠AOB是平角吗?为什么?
O
A
B
C
D
答:是
∵ OA∥CD,OB∥CD
∴OA、OB表示同一条直线
即 点A、O、B在同一条直线上
∴ ∠AOB是平
2、垂直
①垂直的定义及表示方法
定义:如果两条直线相交成直角,那么这两条直线互相垂直。其中一条直线叫做另一条直线的垂线。两条直线的交点叫做垂足。
A
B
C
D
O
“垂直”用符号“⊥”表示.
如图 ,直线AB垂直于直线CD,
记作AB ⊥ CD,垂足为O.
垂直定义的应用:
若直线AB和CD相交,交点为O,∠BOC=90°,则AB⊥CD.这个推理过程可表示为:
∵ ∠BOC=90°
∴ AB⊥CD
2、垂直
①垂直的定义及表示方法
A
B
C
D
O
反之:若两条直线AB⊥CD,垂足为点O,
则∠AOC=∠AOD=∠BOC=∠BOD=90°,
这个推理过程可表示为:
∵ AB⊥CD
∴ ∠BOC=90°
2、垂直
②如何画垂线?(请用三角尺过点P画直线AB的垂线.)
A B
O
P
2、垂直
②如何画垂线?(请用三角尺过点P画直线AB的垂线.)
A
B
P
C
能画几条呢?
一放
二移
三画
2、垂直
③垂线的性质
性质1:过一点有且只有一条直线与已知直线垂直.
性质2 :连接直线外一点与直线上各点的所有线段中,垂线段最短.
简称为“垂线段最短”.
垂线段CF的长度,称为点C 到直线AB 的距离。
C
A
B
F
E
D
G
H
2、垂直
④点到直线的距离
定义:直线外一点到这条直线的垂线段的长度,
叫做点到直线的距离。
C
A
B
F
E
D
G
H
垂线段CF的长度,称为点C 到直线 AB 的距离。
*线段、射线的垂线应怎么画呢?学.科.网
A
B
P
Q
O
A
注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线.
画一条线段或射线的垂线,就是画它们所在直线的垂线
2、垂直
典型例题
例1 如图,污水处理厂要从A处把处理过的水引入排水沟PQ,应如何铺设排水管道,才能使用料最省?试画出铺设管道的路线?并说明理由。
解:从点A向PQ作垂线段AB,垂
足为B,则线段AB就是铺设管
道的路线。
A
Q
P
B
理由:垂线段最短。
例2 如图,P是∠AOB的边OB上一点。
(1)过点P画OB的垂线,交OA于点C;
(2)过点P画OA的垂线,垂足为H。
比较PH与PC、PC与CO的长短,并说明理由。
典型例题
O
P
B
C
H
A
解:PH<PC,PC<CO
理由:垂线段最短。
例3 如图,点O是直线AB上一点,∠AOC=40°,OD平分∠AOC,∠COE=70°.
(1)请你说明DO⊥OE;
(2)OE平分∠BOC吗?为什么?
解(1) ∵OD平分∠AOC
∴ ∠DOC=∠AOC= 20°
∵∠COE=70°
∴∠DOE=90°
∴ DO⊥OE
典型例题
(2)OE平分∠BOC.
∵∠AOC+∠COE+∠BOE=180°
又∵∠AOC=40°,∠COE=70°
∴∠BOE=70°
∴∠BOE=∠COE
∴OE平分∠BOC
例4 一副直角三角板叠放如图①,现将含45°角的三角板ADE 固定不动,把含30°角的三角板ABC绕顶点A顺时针旋转角α(α=∠BAD且0°<α<180°),使两块三角板至少有一组对应边(所在的直线)垂直.
(1)如图②,α= °时,BC⊥AE;
(2)请你在备用图中画一种符合要求的图形,用符号表示出垂直的边,并计算出旋转角α.
典型例题
15
典型例题
使两块三角板至少有一组对应边(所在的直线)垂直.
用符号表示出垂直的边,并计算出旋转角α(∠BAD)
BC⊥AE
α=15°
AC⊥AE
α= °
AC⊥AD
α= °
AB⊥AE
α= °
105
60
135
记作:AB∥CD 读作AB平行于CD
1.在同一平面内不相交的两条直线叫做平行线。
作法:一放、二靠、三移、四画
归纳小结
过直线外一点有且只有一条直线与已知直线平行。
2.过直线外一点做已知直线的平行线
3. 平行线的性质
平行
A
B
C
D
记作:AB⊥CD 读作AB垂直于CD
1.如果两条直线相交成直角,那么这两条直线互相垂直。
其中一条直线叫做另一条直线的垂线。两条直线的交点叫做垂足。
作法:一放、二移、三画
归纳小结
(1)过一点有且只有一条直线与已知直线垂直。
(2)连接直线外一点与直线上各点的所有线段中,垂线段最短。
*这条垂线段的长度叫做点到直线的距离。
2.过一点做已知直线的垂线
3. 垂线的性质
垂直
A
B
C
D
O
?
?
?
?
谢
谢
再
见
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
