苏科版数学七下 8.1 同底数幂的乘法 课件(23张)
文档属性
| 名称 | 苏科版数学七下 8.1 同底数幂的乘法 课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 761.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 09:22:14 | ||
图片预览








文档简介
(共23张PPT)
同底数幂的乘法
高斯(数学王子)说:“数学是科学之王!”
无限风光在险峰
光在真空中的速度约是3×105km/s,光在真空中穿行1年的距离称为1光年.如果1年以3×107s来计算的话,那么1光年=_______________km.
光年:
(3×105 ) ×(3×107)
=(3×3)×(105×107)
那么
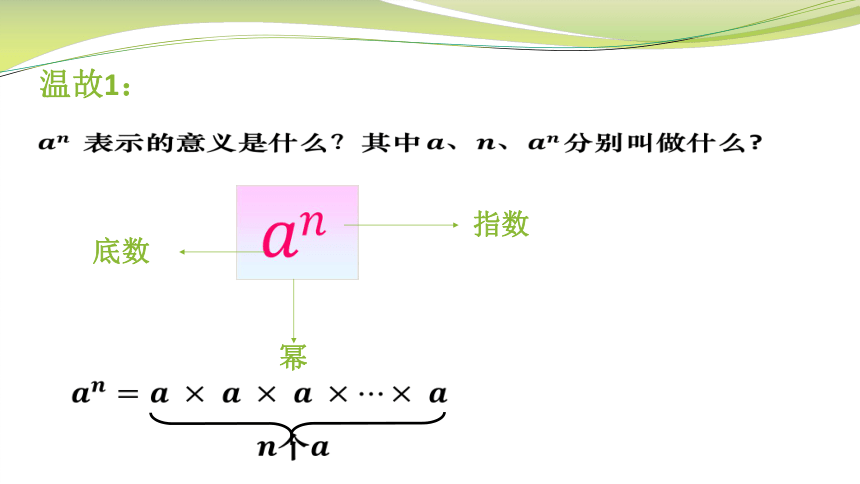
表示的意义是什么?其中分别叫做什么?
底数
幂
指数
温故1:
个
25表示什么?
10×10×10×10×10 可以写成什么形式?
温故2:
25 = .
2×2×2×2×2
105
10×10×10×10×10 = .
1.式子103×102的意义是什么?
思考:
103与102 的积
底数相同
2.这个式子中的两个因式有何特点?
请同学们先根据自己的理解,解答下列各题.
103 ×102 =
(10×10×10)×(10×10)
=10(5)
= 10×10×10×10×10
104×105 =
(10×10×10×10)×(10×10×10×10×10)
= 10×10×10×10×10×10×10×10×10
= 10(9)
105×107
=10(12)
2.怎样计算
探索活动
3.当是正整数时, 等于什么?
呢?
探索活动
猜想: (当都是正整数)
=
个
个
=
=
个
即
(当都是正整数)
()
· ()
(乘方的意义)
(乘法结合律)
(乘方的意义)
同底数幂相乘,底数不变,指数相加.
同底数幂的乘法运算性质
是正整数,你会计算吗?
(2)
(3)
例1.计算
(1)
(4)
注:幂的底数不仅仅是单独字母或数字,也可以是某个单项式或多项式.
指数是“1”
(5)
例题讲解
1.计算(口答)
(1)
(2)
(3)
(4)
随堂练习
2.下面的计算是否正确?若有错误,应该怎样改正?
(1)
(2)
(3)
(4)
(5)
(6)
随堂练习
例2 计算:
;
34×9×81(结果用幂的形式表示)
解:
先转化为同底数的幂的形式再进行计算.
34×9×81
= 34×32×34
= 34+2+4
=310;
例题讲解
例 2 计算:
解
,(为偶数)
,(为奇数)
例题讲解
3.计算
(1)
(2)
4.填空
(1)=
5
(2)=
随堂练习
(1)
(2)
计算
能力拓展
例3 (1)已知,,求的值.
解:∵,
又
∴ .
(2)已知3+1=81,求.
=3
例题讲解
计算:
; ;
; ;
练一练
计算:
(5) 103×10+100×102; (6)8×2×16;
(7) 9×27-3×34; (8) .
练一练
计算: (-2)2012-22011 .
解:原式=22012-22011
=2×22011-22011
=(2-1)×22011
=22011 .
深度思维
同底数幂相乘,底数 指数
(正整数)
我的收获
知识
方法
特殊 → 一般 → 特殊
例子 公式 应用
不变,
相加.
→
→
通过这节课的学习,我学到了:
总结与回顾
谢 谢
同底数幂的乘法
高斯(数学王子)说:“数学是科学之王!”
无限风光在险峰
光在真空中的速度约是3×105km/s,光在真空中穿行1年的距离称为1光年.如果1年以3×107s来计算的话,那么1光年=_______________km.
光年:
(3×105 ) ×(3×107)
=(3×3)×(105×107)
那么
表示的意义是什么?其中分别叫做什么?
底数
幂
指数
温故1:
个
25表示什么?
10×10×10×10×10 可以写成什么形式?
温故2:
25 = .
2×2×2×2×2
105
10×10×10×10×10 = .
1.式子103×102的意义是什么?
思考:
103与102 的积
底数相同
2.这个式子中的两个因式有何特点?
请同学们先根据自己的理解,解答下列各题.
103 ×102 =
(10×10×10)×(10×10)
=10(5)
= 10×10×10×10×10
104×105 =
(10×10×10×10)×(10×10×10×10×10)
= 10×10×10×10×10×10×10×10×10
= 10(9)
105×107
=10(12)
2.怎样计算
探索活动
3.当是正整数时, 等于什么?
呢?
探索活动
猜想: (当都是正整数)
=
个
个
=
=
个
即
(当都是正整数)
()
· ()
(乘方的意义)
(乘法结合律)
(乘方的意义)
同底数幂相乘,底数不变,指数相加.
同底数幂的乘法运算性质
是正整数,你会计算吗?
(2)
(3)
例1.计算
(1)
(4)
注:幂的底数不仅仅是单独字母或数字,也可以是某个单项式或多项式.
指数是“1”
(5)
例题讲解
1.计算(口答)
(1)
(2)
(3)
(4)
随堂练习
2.下面的计算是否正确?若有错误,应该怎样改正?
(1)
(2)
(3)
(4)
(5)
(6)
随堂练习
例2 计算:
;
34×9×81(结果用幂的形式表示)
解:
先转化为同底数的幂的形式再进行计算.
34×9×81
= 34×32×34
= 34+2+4
=310;
例题讲解
例 2 计算:
解
,(为偶数)
,(为奇数)
例题讲解
3.计算
(1)
(2)
4.填空
(1)=
5
(2)=
随堂练习
(1)
(2)
计算
能力拓展
例3 (1)已知,,求的值.
解:∵,
又
∴ .
(2)已知3+1=81,求.
=3
例题讲解
计算:
; ;
; ;
练一练
计算:
(5) 103×10+100×102; (6)8×2×16;
(7) 9×27-3×34; (8) .
练一练
计算: (-2)2012-22011 .
解:原式=22012-22011
=2×22011-22011
=(2-1)×22011
=22011 .
深度思维
同底数幂相乘,底数 指数
(正整数)
我的收获
知识
方法
特殊 → 一般 → 特殊
例子 公式 应用
不变,
相加.
→
→
通过这节课的学习,我学到了:
总结与回顾
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
