苏科版数学七下 8.2 幂的乘方与积的乘方(1) 课件(23张)
文档属性
| 名称 | 苏科版数学七下 8.2 幂的乘方与积的乘方(1) 课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 878.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
幂的乘方与积的乘方(1)
填空:
1. =_____,依据________________.
2. =____ ,依据_______________________.
3. 若=8,=30,则=_______.
合并同类项法则
同底数幂乘法的法则
240
知识回顾
请一位同学在黑板上写下100个104的乘积,谁能有简便的写法呢?
根据乘方的定义,100个104相乘,
可以写成 (104)100 .你会计算吗?
做一做
先说出下列各式的意义,再计算下列各式:
(23)2表示____________;
()3表示____________;
()5表示____________;
上面各式括号中都是 的形式,
然后再 .
你能给这种运算起个名字吗?
幂
乘方
26
2个23相乘
3个相乘
5个相乘
做一做
幂的乘方
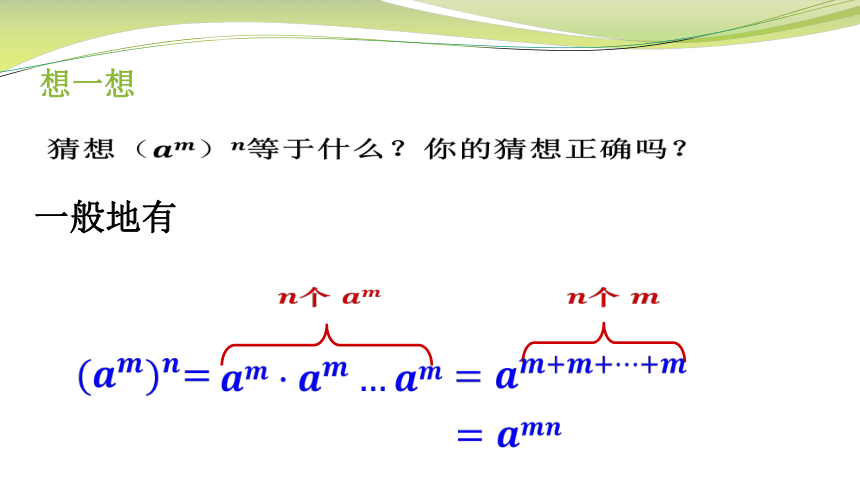
猜想等于什么?你的猜想正确吗?
一般地有
个
个
想一想
幂的乘方,底数不变,指数相乘。
幂的乘方法则:
注意:
1.公式中的底数可以是具体的数,也可以是代数式.
2.注意幂的乘方中指数相乘,
而同底数幂的乘法中是指数相加.
,其中是正整数
(4)
解:
(3)
(5)
(6)
(1)
(2)
注意符号
(1) (2) (3)
(4) (5) (6)
例 1? 计算:
思考: (为正整数),对吗?
当为奇数时, (为正整数)
当为偶数时, (为正整数)
1.计算 (102)3 (5)5 ()3 -()
106
2.计算 (104)2 (5)4 -(2)5 (-23)20
3.下面的计算是否正确?如有错误请改正.
(1) (2)
108
260
练一练
5.下列计算中正确的个数有(?? )个
①.?????????②.
③.???????????④.
(A)1个 (B)2个 (C)3个 (D)以上答案都不对
D
4.填空:
(1)108=( )2; (2)( );
(3)=( ); (4)=( )2.
104
9
(2)
例 2?计算:
(1)
(2)
解:(1)
例2 计算:
; (是正整数).
解: (3)原式
(4)原式
---①幂的乘方
---② 同底数幂相乘
---③合并同类项
幂的乘方公式逆用:
⑴ 215×25=
⑵ 215×8=
⑶ 215×85=
215+5=220
215×23
=218
215×(23)5
=215×215
=230
解法二:原式=(23)5×85
=85×85
=810
计算(结果用幂的形式表示)
=(23)10
=230
转化为同底数幂
=(23)10
=810
转化为同指数幂
解:∵230=23×10
例3.比较230与320的大小
=(23)10
320=32×10
=(32)10
又∵23=8,32=9
而8<9
∴230<320
幂的乘方公式逆用:
比较3555、4444、5333的大小,
解:∵3555=35×111=(35)111=243111,
4444=44×111=(44)111=256111,
5333=53×111=(53)111=125111,
又256>243>125,
∴ 5333<3555<4444
深度思维
解: ∵,
∴
例4.若,,求的值.
=33×52
=675.
幂的乘方公式逆用:
1、计算
(1) (2)
解(1)原式
(2)原式
(3)(-32)3(-33)2 (4)
(3)解:原式= -3636
= -312
(4)解:原式
练一练
2、下列计算是否正确,如有错误,请改正.
⑴;
⑵;
⑶;
⑷;
⑸(是正整数);
⑹(是正整数).
√
无法计算
练一练
(1)若,求
(2)若 , , 求
练一练
3、解答
(3)比较2100与375的大小.
(4)已知求的值.
这节课,我的收获是---
小结与回顾
知识
能力
计算和推理能力
逆向思维
比较的方法
特殊到一般的方法
知识树
幂的乘方
思想方法
例题4
第4题
公式应用
例题1、2
这节课,我的收获是---
方程的思想
化归的思想
例3
谢 谢
幂的乘方与积的乘方(1)
填空:
1. =_____,依据________________.
2. =____ ,依据_______________________.
3. 若=8,=30,则=_______.
合并同类项法则
同底数幂乘法的法则
240
知识回顾
请一位同学在黑板上写下100个104的乘积,谁能有简便的写法呢?
根据乘方的定义,100个104相乘,
可以写成 (104)100 .你会计算吗?
做一做
先说出下列各式的意义,再计算下列各式:
(23)2表示____________;
()3表示____________;
()5表示____________;
上面各式括号中都是 的形式,
然后再 .
你能给这种运算起个名字吗?
幂
乘方
26
2个23相乘
3个相乘
5个相乘
做一做
幂的乘方
猜想等于什么?你的猜想正确吗?
一般地有
个
个
想一想
幂的乘方,底数不变,指数相乘。
幂的乘方法则:
注意:
1.公式中的底数可以是具体的数,也可以是代数式.
2.注意幂的乘方中指数相乘,
而同底数幂的乘法中是指数相加.
,其中是正整数
(4)
解:
(3)
(5)
(6)
(1)
(2)
注意符号
(1) (2) (3)
(4) (5) (6)
例 1? 计算:
思考: (为正整数),对吗?
当为奇数时, (为正整数)
当为偶数时, (为正整数)
1.计算 (102)3 (5)5 ()3 -()
106
2.计算 (104)2 (5)4 -(2)5 (-23)20
3.下面的计算是否正确?如有错误请改正.
(1) (2)
108
260
练一练
5.下列计算中正确的个数有(?? )个
①.?????????②.
③.???????????④.
(A)1个 (B)2个 (C)3个 (D)以上答案都不对
D
4.填空:
(1)108=( )2; (2)( );
(3)=( ); (4)=( )2.
104
9
(2)
例 2?计算:
(1)
(2)
解:(1)
例2 计算:
; (是正整数).
解: (3)原式
(4)原式
---①幂的乘方
---② 同底数幂相乘
---③合并同类项
幂的乘方公式逆用:
⑴ 215×25=
⑵ 215×8=
⑶ 215×85=
215+5=220
215×23
=218
215×(23)5
=215×215
=230
解法二:原式=(23)5×85
=85×85
=810
计算(结果用幂的形式表示)
=(23)10
=230
转化为同底数幂
=(23)10
=810
转化为同指数幂
解:∵230=23×10
例3.比较230与320的大小
=(23)10
320=32×10
=(32)10
又∵23=8,32=9
而8<9
∴230<320
幂的乘方公式逆用:
比较3555、4444、5333的大小,
解:∵3555=35×111=(35)111=243111,
4444=44×111=(44)111=256111,
5333=53×111=(53)111=125111,
又256>243>125,
∴ 5333<3555<4444
深度思维
解: ∵,
∴
例4.若,,求的值.
=33×52
=675.
幂的乘方公式逆用:
1、计算
(1) (2)
解(1)原式
(2)原式
(3)(-32)3(-33)2 (4)
(3)解:原式= -3636
= -312
(4)解:原式
练一练
2、下列计算是否正确,如有错误,请改正.
⑴;
⑵;
⑶;
⑷;
⑸(是正整数);
⑹(是正整数).
√
无法计算
练一练
(1)若,求
(2)若 , , 求
练一练
3、解答
(3)比较2100与375的大小.
(4)已知求的值.
这节课,我的收获是---
小结与回顾
知识
能力
计算和推理能力
逆向思维
比较的方法
特殊到一般的方法
知识树
幂的乘方
思想方法
例题4
第4题
公式应用
例题1、2
这节课,我的收获是---
方程的思想
化归的思想
例3
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
