苏科版数学七下8.2 幂的乘方与积的乘方(2) 课件(28张)
文档属性
| 名称 | 苏科版数学七下8.2 幂的乘方与积的乘方(2) 课件(28张) |  | |
| 格式 | zip | ||
| 文件大小 | 924.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 09:11:27 | ||
图片预览




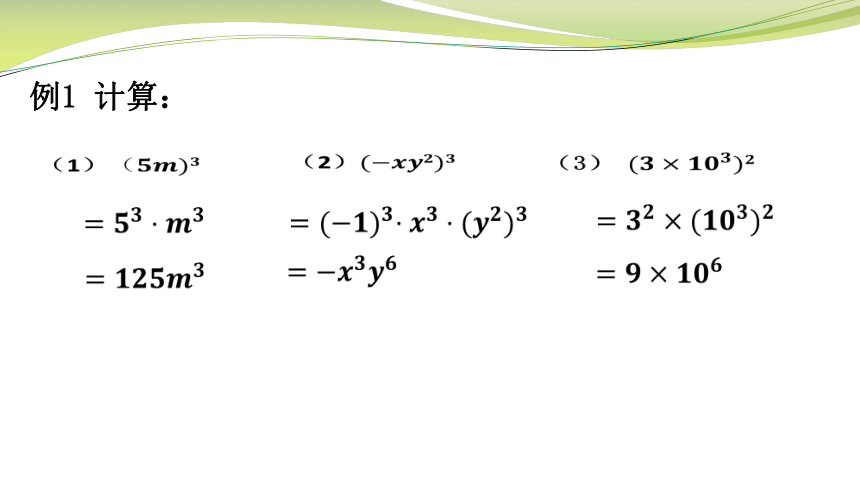


文档简介
(共28张PPT)
幂的乘方与积的乘方(2)
① ( )
② ______( )
③ ( )
同底数幂相乘
幂的乘方
乘法交换律、结合律
正确写出得数,并说出是属于哪一种幂的运算。
知识回顾
思考题:
1、若,则=_____.
2、若,,
则=_______, =_______.
8
6
72
动脑筋!
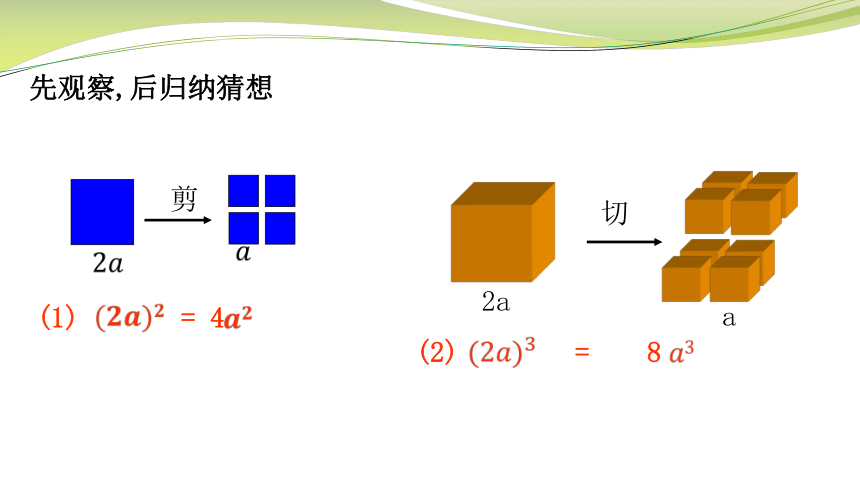
先观察,后归纳猜想
切
(1) = 4
a
2a
剪
(2) = 8
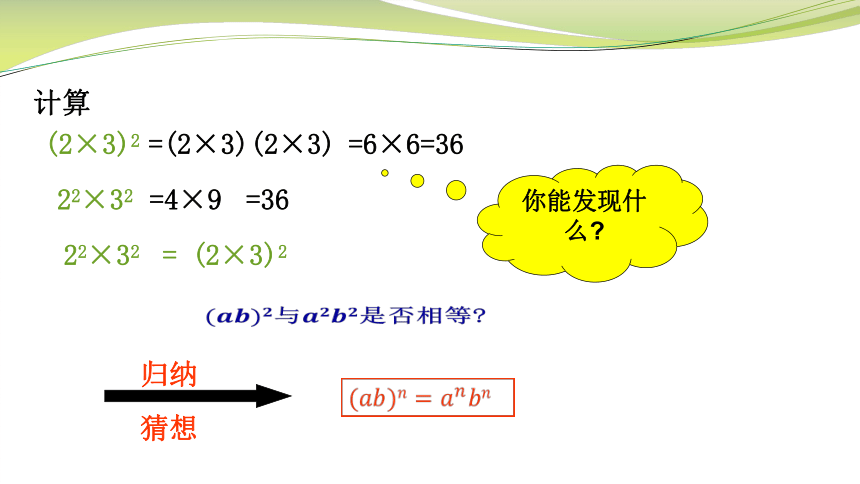
计算
22×32
=4×9
=36
(2×3)2
=(2×3)(2×3)
=6×6=36
你能发现什么?
22×32
= (2×3)2
与是否相等?
归纳
猜想
公式证明
个
(乘方的意义)
(单项式的乘法法则)
个
个
(乘方的意义)
即
你能用语言表述
积的乘方法则吗?
积的乘方法则:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘。
拓展 当三个或三个以上因式的积乘方时, 也具有这一性质
例如
例1 计算:
(1)
(2)
(3)
1、口答:(1) =( ) (2)=( )
(3)=( ) (4)= ( )
(5)=( ) (6)=( )
(7)=( ) (8) =( )
2、下面的计算对不对?如果不对,应怎样改正?
(1); (2);
(3); (4);
(5)
×
×
×
×
√
练一练
3、以下三组运算正确的是:
A. B.
C. D.
A. B.
C. D.
A. B.
C. D.
例2 计算:
解法1:原式
解法2:原式
原来积的乘方法则可以逆用
即
巧学巧用
公式的反向使用
(都是正整数)
反向使用:
(1) 28×58
(2) (-5)16 ×(-2)15
(3) 24 ×44×(-0.125)4
= (2×5)8
= 108
=(-5)×(-5)15×(-2)15
=(-5)×[(-5)×(-2)]15
= -5×1015
=[2×4×(-0.125)]4
=14
=1
公式反向使用的前提:指数相同
我也来试试
二、计算:
一、脱口而出:
(1) ; (2)
例3 (1)在手工课上,小军制作了一个正方形的模具,其边长是,问该模具的体积是多少?
解:(4×103)3
= 43×(103 )3
= 64×109
= 6.4×1010
答:该模具的体积为6.4×1010㎝3
生活中的应用
例3 (2)地球可以近视地看作是球体,如果用V、r表示球的体积和半径,那么V=,地球半径是6×103千米,它的体积大约是多少立方千米?(π取3.14)
解: V=
答:地球的体积大约是9.04×1011立方千米。
1、计算:
(-3n)3 ; (2) (5xy)3 ;
(3) –a3 +(–4a)2 a (4) a5a3+(–2a2)3
2、下面的计算是否正确?如果有错误,请改正.
( )
( )
随堂练习
(3)请用简便的方法计算下列各题:
随堂练习
(4)若, , 求的值.
幂运算中的易错点
1.注意符号问题
2.注意幂的性质的混淆和错误
3. 注意幂的运算法则逆用
1.注意符号问题
例1 判断下列等式是否成立:
① ,
② ,
③ ,
④ ,
⑤ ,
⑥ .
√
√
√
√
×
×
2.注意幂的性质的混淆和错误
3. 注意幂的运算法则逆用
(为正整数),
(1)巧算
计算:
1、(-4)2007×0.252008
2、22006-22005-22004-…-2-1
(2)比较实数的大小
比较750与4825的大小.
(3)求代数式的值
1、已知,.求的值.
2、已知,,
求的值。
在数学活动中,小明为了求的值,
设计如图(1)所示的几何图形。
(1)请你利用这个几何图形求 的值为 。
图(1)
动手合作:
本节课你学到了什么?
{
幂的意义:
a·a· … ·a
n个
an
=
同底数幂的乘法运算法则:
am · an=am+n
幂的乘方运算法则: (ab)n=anbn
积的乘方= .
反向使用am · an =am+n、(am)n =amn 可使某些计算简捷。
每个因式分别乘方后的积
谢 谢
幂的乘方与积的乘方(2)
① ( )
② ______( )
③ ( )
同底数幂相乘
幂的乘方
乘法交换律、结合律
正确写出得数,并说出是属于哪一种幂的运算。
知识回顾
思考题:
1、若,则=_____.
2、若,,
则=_______, =_______.
8
6
72
动脑筋!
先观察,后归纳猜想
切
(1) = 4
a
2a
剪
(2) = 8
计算
22×32
=4×9
=36
(2×3)2
=(2×3)(2×3)
=6×6=36
你能发现什么?
22×32
= (2×3)2
与是否相等?
归纳
猜想
公式证明
个
(乘方的意义)
(单项式的乘法法则)
个
个
(乘方的意义)
即
你能用语言表述
积的乘方法则吗?
积的乘方法则:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘。
拓展 当三个或三个以上因式的积乘方时, 也具有这一性质
例如
例1 计算:
(1)
(2)
(3)
1、口答:(1) =( ) (2)=( )
(3)=( ) (4)= ( )
(5)=( ) (6)=( )
(7)=( ) (8) =( )
2、下面的计算对不对?如果不对,应怎样改正?
(1); (2);
(3); (4);
(5)
×
×
×
×
√
练一练
3、以下三组运算正确的是:
A. B.
C. D.
A. B.
C. D.
A. B.
C. D.
例2 计算:
解法1:原式
解法2:原式
原来积的乘方法则可以逆用
即
巧学巧用
公式的反向使用
(都是正整数)
反向使用:
(1) 28×58
(2) (-5)16 ×(-2)15
(3) 24 ×44×(-0.125)4
= (2×5)8
= 108
=(-5)×(-5)15×(-2)15
=(-5)×[(-5)×(-2)]15
= -5×1015
=[2×4×(-0.125)]4
=14
=1
公式反向使用的前提:指数相同
我也来试试
二、计算:
一、脱口而出:
(1) ; (2)
例3 (1)在手工课上,小军制作了一个正方形的模具,其边长是,问该模具的体积是多少?
解:(4×103)3
= 43×(103 )3
= 64×109
= 6.4×1010
答:该模具的体积为6.4×1010㎝3
生活中的应用
例3 (2)地球可以近视地看作是球体,如果用V、r表示球的体积和半径,那么V=,地球半径是6×103千米,它的体积大约是多少立方千米?(π取3.14)
解: V=
答:地球的体积大约是9.04×1011立方千米。
1、计算:
(-3n)3 ; (2) (5xy)3 ;
(3) –a3 +(–4a)2 a (4) a5a3+(–2a2)3
2、下面的计算是否正确?如果有错误,请改正.
( )
( )
随堂练习
(3)请用简便的方法计算下列各题:
随堂练习
(4)若, , 求的值.
幂运算中的易错点
1.注意符号问题
2.注意幂的性质的混淆和错误
3. 注意幂的运算法则逆用
1.注意符号问题
例1 判断下列等式是否成立:
① ,
② ,
③ ,
④ ,
⑤ ,
⑥ .
√
√
√
√
×
×
2.注意幂的性质的混淆和错误
3. 注意幂的运算法则逆用
(为正整数),
(1)巧算
计算:
1、(-4)2007×0.252008
2、22006-22005-22004-…-2-1
(2)比较实数的大小
比较750与4825的大小.
(3)求代数式的值
1、已知,.求的值.
2、已知,,
求的值。
在数学活动中,小明为了求的值,
设计如图(1)所示的几何图形。
(1)请你利用这个几何图形求 的值为 。
图(1)
动手合作:
本节课你学到了什么?
{
幂的意义:
a·a· … ·a
n个
an
=
同底数幂的乘法运算法则:
am · an=am+n
幂的乘方运算法则: (ab)n=anbn
积的乘方= .
反向使用am · an =am+n、(am)n =amn 可使某些计算简捷。
每个因式分别乘方后的积
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
