人教新课标版高中物理必修二达标作业 平抛运动 Word版含解析
文档属性
| 名称 | 人教新课标版高中物理必修二达标作业 平抛运动 Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 185.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-30 10:45:31 | ||
图片预览



文档简介
1.决定平抛物体落地点与抛出点间水平距离的因素是( )
A.初速度
B.抛出时物体的高度
C.抛出时物体的高度和初速度
D.物体的质量和初速度
[解析] 物体做平抛运动,水平方向上有x=v0t,竖直方向上有h=gt2,解得x=v0,所以落地点与抛出点间水平距离由抛出时物体的高度和初速度决定,选项C正确.
[答案] C
2.某人站在平台上平抛一小球,球离手时的速度为v1,落地时的速度为v2,不计空气阻力,图中能表示出速度矢量演变过程的是( )
[解析] 做平抛运动的物体加速度恒为g,则速度的变化量Δv=gΔt,方向始终竖直向下,故选项C正确.
[答案] C
3.如图所示,滑板运动员以速度v0从离地高h处的平台末端水平飞出,落在水平地面上.忽略空气阻力,运动员和滑板可视为质点,下列表述正确的是( )
A.v0越大,运动员在空中运动的时间越长
B.v0越大,运动员落地的瞬时速度越大
C.运动员落地的瞬时速度与高度h无关
D.运动员落地的位置与v0大小无关
[解析] 运动员从平台水平飞出后做平抛运动,故在竖直方向做自由落体运动,在空中运动的时间t=,只与高度有关,与初速度v0无关,A项错误;运动员落地时的瞬时速度是由初速度和落地时竖直方向上的分速度合成的,合速度v=,初速度越大,合速度越大,B项正确;运动员落地瞬间在竖直方向上的分速度vy=,高度越高,落地时竖直方向上的分速度越大,合速度越大,C项错误;运动员在水平方向上做匀速直线运动,落地的水平位移x=v0t=v0,故落地的位置与初速度v0有关,D项错误.
[答案] B
4.(多选)关于斜上抛运动,下列说法中正确的是( )
A.物体抛出后,速度增大,加速度减小
B.物体抛出后,速度先减小,再增大
C.物体抛出后,加速度始终沿着切线方向
D.斜上抛运动的物体做匀变速曲线运动
[解析] 斜上抛运动的加速度为重力加速度,大小方向不变,速度先减小再增大,选项B、D正确.
[答案] BD
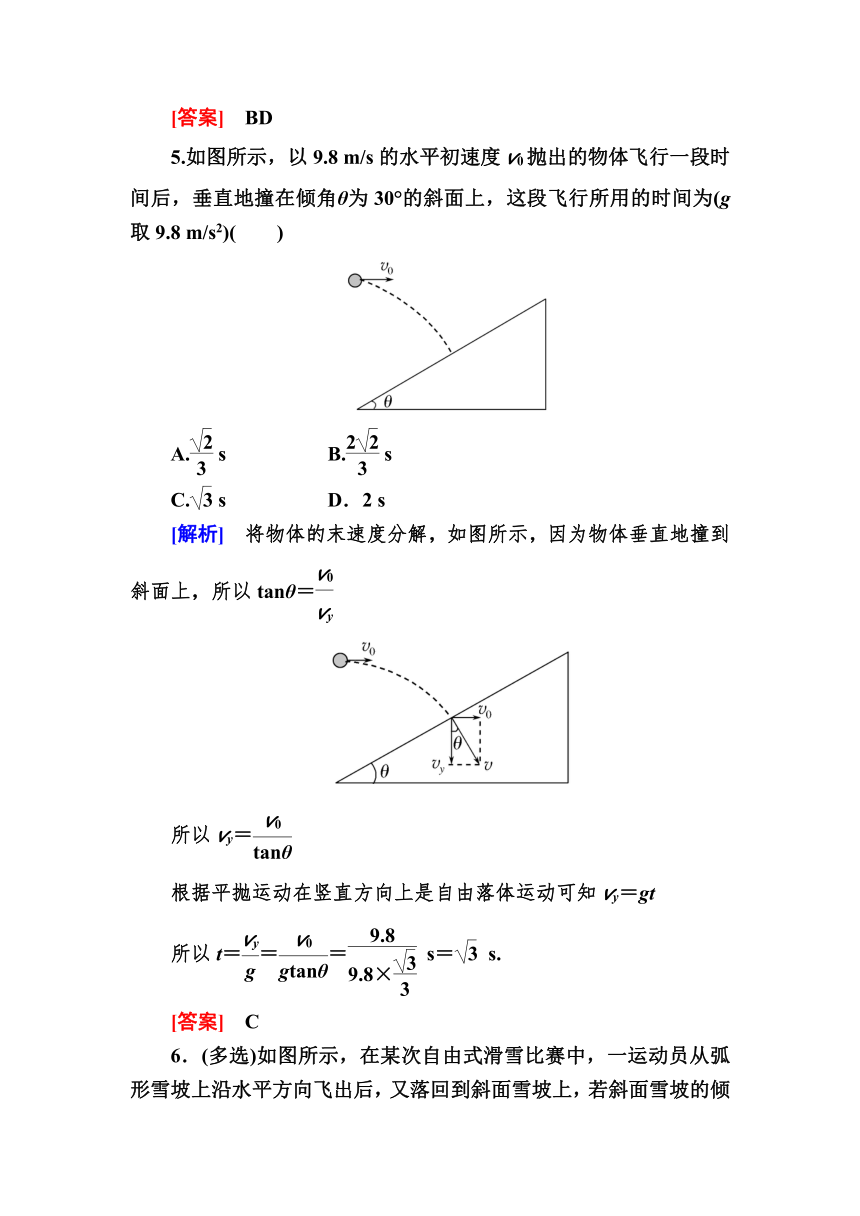
5.如图所示,以9.8 m/s的水平初速度v0抛出的物体飞行一段时间后,垂直地撞在倾角θ为30°的斜面上,这段飞行所用的时间为(g取9.8 m/s2)( )
A. s B. s
C. s D.2 s
[解析] 将物体的末速度分解,如图所示,因为物体垂直地撞到斜面上,所以tanθ=
所以vy=
根据平抛运动在竖直方向上是自由落体运动可知vy=gt
所以t=== s= s.
[答案] C
6.(多选)如图所示,在某次自由式滑雪比赛中,一运动员从弧形雪坡上沿水平方向飞出后,又落回到斜面雪坡上,若斜面雪坡的倾角为θ,飞出时的速度大小为v0,不计空气阻力,运动员飞出后在空中的姿势保持不变,重力加速度为g,则( )
A.如果v0不同,则该运动员落到雪坡时的速度方向也就不同
B.不论v0多大,该运动员落到雪坡时的速度方向都是相同的
C.运动员落到雪坡时的速度大小是
D.运动员在空中经历的时间是
[解析] 如果v0不同,则该运动员落到雪坡时的位置不同,但位移方向均沿斜坡,即位移方向与水平方向的夹角均为θ,设落到雪坡时速度方向与水平方向的夹角为φ,则tanφ=2tanθ,得速度方向与水平方向的夹角均为φ,故A错误,B正确;将运动员落到雪坡时的速度沿水平和竖直方向分解,求出运动员落到雪坡时的速度大小为,故C错误;由几何关系得tanθ=,解出运动员在空中经历的时间t=,故D正确.
[答案] BD
[拓展提升]
7.(多选)如图所示,从某高度水平抛出一小球,经过时间t小球到达地面时,速度与水平方向的夹角为θ,不计空气阻力,重力加速度为g.下列说法正确的是( )
A.小球水平抛出时的初速度大小为gttanθ
B.小球着地时速度大小为
C.小球在t时间内的位移方向与水平方向的夹角为
D.若小球初速度增大,则θ减小
[解析] 将小球着地时的速度进行分解,如图所示:
可知tanθ=,所以v0=,选项A错误.着地时速度大小v==,选项B正确.设t时间内的位移方向与水平方向的夹角为α,则tanα====tanθ,选项C错误.tanθ=,t不变,当初速度v0增大时,tanθ变小,θ变小,选项D正确.
[答案] BD
8.如图所示,从倾角为θ的足够长的斜面顶端P处以水平速度v0抛出一个小球,小球落在斜面上某处Q点,落在斜面上的速度方向与斜面间的夹角为α,若把小球初速度变为原来的倍,则下列说法正确的是( )
A.小球在空中运动时间变为原来的2倍
B.落在斜面上的速度方向与斜面间的夹角大于α
C.抛出点到落到斜面上的点的距离一定等于PQ的4倍
D.落在斜面上的速度方向与斜面间的夹角等于α
[解析] 由tanθ===可知,小球在空中运动时间变为原来的倍,抛出点到落到斜面上的点的距离为PQ的2倍,水平速度与竖直速度的比值不变,故合速度方向不变,可得落在斜面上的速度方向与斜面间的夹角等于α,故D正确,A、B、C错误.
[答案] D
9.如图所示,一小球自平台上水平抛出,恰好落在临近平台的一倾角为α=53°的光滑斜面顶端,并刚好沿光滑斜面下滑,已知斜面顶端与平台的高度差h=0.2 m,重力加速度g取10 m/s2,sin53°=0.8,cos53°=0.6,求:
(1)小球水平抛出的初速度v0是多少?
(2)斜面顶端与平台边缘的水平距离x是多少?
[解析] (1)由题意可知,小球落到斜面上并沿斜面下滑,说明此时小球速度方向与斜面平行,否则小球会弹起,则
vy=v0tan53°
v=2gh
代入数据,得vy=2 m/s,v0=1.5 m/s.
(2)由vy=gt1得t1=0.2 s
x=v0t1=1.5×0.2 m=0.3 m.
[答案] (1)1.5 m/s (2)0.3 m
10.如图所示,光滑斜面长为L=10 m,倾角为30°,一小球从斜面的顶端以v0=10 m/s的初速度水平射入,求:(g取10 m/s2)
(1)小球沿斜面运动到底端时的水平位移x;
(2)小球到达斜面底端时的速度大小.
[解析] (1)小球在斜面上沿v0方向做匀速直线运动,沿垂直于v0方向做初速度为零、加速度为a的匀加速直线运动.根据牛顿第二定律有mgsin30°=ma,又L=at2,解得t= ,所以水平位移x=v0t=v0 =20 m.
(2)设小球运动到斜面底端时的速度为v,则有
vx=v0=10 m/s,v=2aL=2gsin30°·L=gL=100 m2/s2
故v==10 m/s.
[答案] (1)20 m (2)10 m/s
[强力纠错]
11.(多选)将一个物体从h高处以水平初速度v0抛出,物体落地时的速度为v,竖直分速度为vy,下列公式能用来表示该物体在空中运动时间的是( )
A. B.
C. D.
[解析] 平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动,设物体从抛出到落地经历的时间为t.
水平方向位移为x=v0t
竖直方向位移为h=gt2,竖直分速度为vy=gt
则竖直方向的位移为h=t
合速度与分速度大小关系为v=v2-v
由以上各式可知,选项A、C、D正确.
[答案] ACD
12.(多选)从正在高空水平匀速飞行的飞机上每隔1 s释放1个小球,先后共释放5个,不计空气阻力,则( )
A.这5个小球在空中处在同一条竖直线上
B.这5个小球在空中处在同一条抛物线上
C.在空中,第1、2两球间的距离保持不变
D.相邻两球的落地间距相等
[解析] 释放的每个小球都做平抛运动,水平速度与飞机的飞行速度相等,每个小球落地前都位于飞机的正下方,即处在同一条竖直线上,如图所示.
第1、2两球在空中的间距为
Δh=g(t+1)2-gt2=g(2t+1)
可见,Δh随时间的增加而增大.
相邻两球落地时的间距为
Δx=v0(t+1)-v0t=v0
可见,Δx与下落时间无关.综上所述,本题正确选项为A、D.
[答案] AD
