苏科版数学七下 9.4 乘法公式(2) 课件(23张)
文档属性
| 名称 | 苏科版数学七下 9.4 乘法公式(2) 课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
乘法公式(2)
学习目标
能推导平方差公式,了解公式的几何背景,并能利用公式进行简单计算;
经历探索平方差公式的过程,进一步感悟数与形的关系,感悟数形结合的思想。
完全平方公式:
(a b)2=a2 +b2
(a b)2=a2 +b2
公式再现
计算:(a+b+c)2
2ab
2ab
+
+
-
-
( a + b )2= a2 + 2 a b + b2
( + )2 = 2 + 2· · + 2
?
?
?
?
?
?
c
c
c
a+b
a+b
a+b
= [(a+b) +c]2
= a2+2ab+b2+2ac+2bc+c2
= (a+b)2+2·(a+b)·c+c2
= a2+b2+c2+2ab+2bc+2ac
计算:(a+b+c)2
(a+b+c)2=(a+b+c)(a+b+c)
= a2+b2+c2+2ab+2bc+2ac
代数方法:多项式×多项式
= a2+ab+ac
+ab+b2+bc
+ac+bc+c2
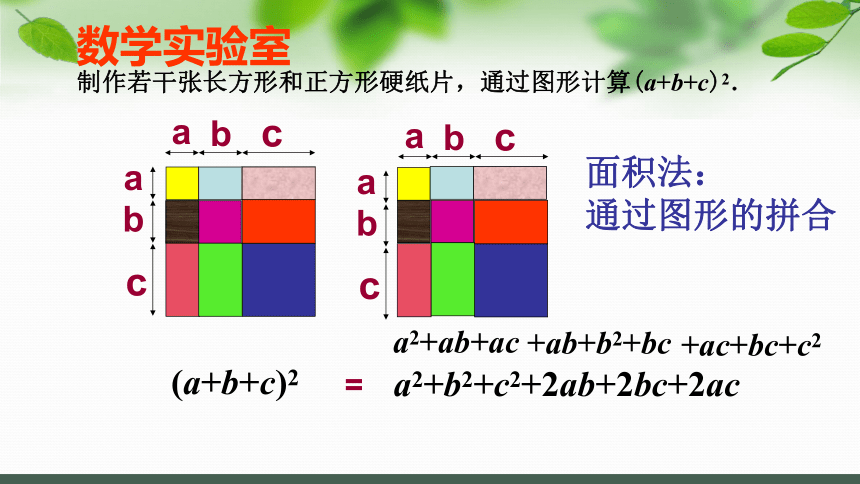
面积法:
通过图形的拼合
a
b
c
c
b
a
=
制作若干张长方形和正方形硬纸片,通过图形计算(a+b+c)2.
数学实验室
(a+b+c)2
a2+b2+c2+2ab+2bc+2ac
a2+ab+ac
+ab+b2+bc
+ac+bc+c2
a
b
c
c
b
a
完全平方公式:(a b)2=a2 +b2
(a b)2=a2 +b2
公式再现
2ab
2ab
+
+
-
-
(a+b+c)2= a2+b2+c2+2ab+2bc+2ac
练习:(m+n-t)2
=m2+n2+t2+2mn-2mt-2nt
计算 (1) (x+y) (x-y)
(2) (a+1) (a-1)
(3) (mn+a) (mn-a)
练一练
(x+y) (x-y) =x2﹣y2
(a+1) (a-1) =a2﹣1
(mn+a) (mn-a) =m2n2 ﹣a2
=x2 ﹣xy +xy - y2
=x2﹣y2
=a2﹣a +a - 1
=a2﹣1
= m2n2 ﹣mna +mna - a2
=m2n2﹣a2
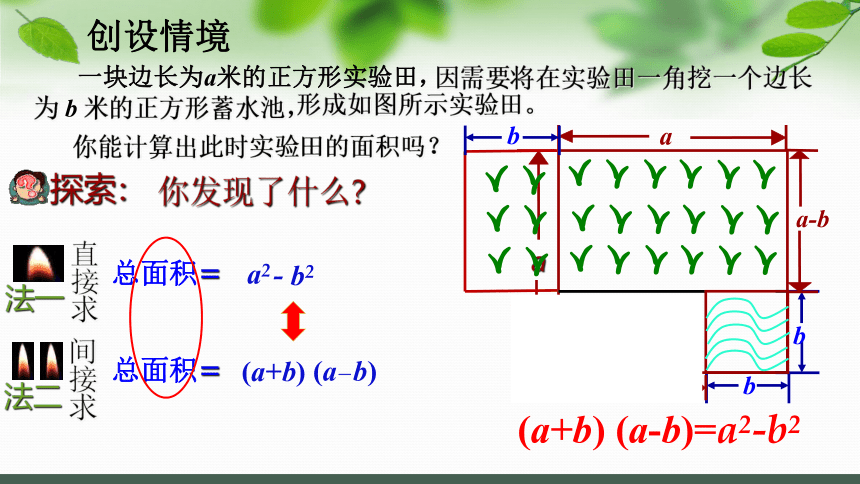
一块边长为a米的正方形实验田,
a
因需要将在实验田一角挖一个边长为 b 米的正方形蓄水池,
形成如图所示实验田。
你能计算出此时实验田的面积吗?
a
b
b
法一
直
接
求
总面积=
法二
间
接
求
总面积=
(a+b) (a-b)=a2-b2
你发现了什么?
探索:
a2
- b2
创设情境
(a-b)
(a+b)
a-b
b
a-b
a
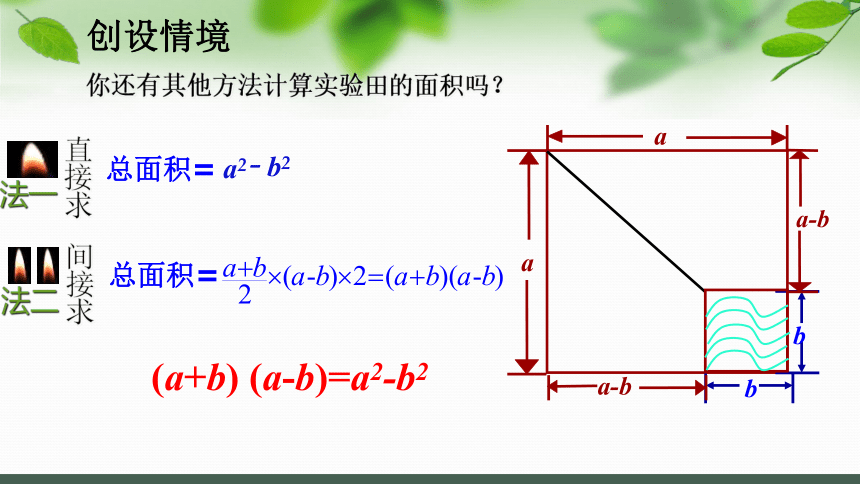
你还有其他方法计算实验田的面积吗?
a
b
b
法一
直
接
求
总面积=
法二
间
接
求
总面积=
a2
﹣b2
创设情境
a-b
a-b
(a+b) (a-b)=a2-b2
(a+b) (a-b) =a2 - b2
(a+b) (a-b) =
推证 ?
a2-ab+
ab-b2
= a2
- b2
上面的等式是利用面积的不同表示形式得到的,你还有其他方法吗?
探索
左边是:
的积;
右边是:
两个数和与
a
a
两个数的平方差
几
何
背景
两个数的和与这两个数的差的积等于这两个数的平方差.
两个数差
b
b
(a+b)(a?b)/2
(a+b) (a?b)
= a2?b2
初识 平方差公式
(a+b) (a-b) =a2 - b2
(a+b)(a?b)/2
说说这个公式的特点:
文字表述:
用自己的语言叙述上面的公式
平方差公式
(a+b) (a-b)=a2-b2
公式的文字表述:
两个数的和与这两个数的差的积等于这两个数的平方差.
新知
(y+5) (-y-5)
(5-y) (5+y)
?
?
(a+b) (a-b)=a2-b2
(?+?) (?-?) =?2-?2
( + ) ( - )
下列各式具有可以利用平方差公式计算的特征吗?
(1) (x+2y) (2x-y)
(2) (m-n) (n+m)
(3) (c+d) (-d-c)
(4) (2a+b) (2a-c)
辩一辩
( + ) ( - )
利用平方差公式计算,第一步先 明确是哪个数是a、哪个数是b ;第二步准确代入公式;第三步化简。
例1 用平方差公式计算:
(1) ( 5x + y ) ( 5x - y) (2) (m+2n) (2n-m )
解: (1) ( 5x + y ) ( 5x - y)
=25x2 - y2
典型例题
= ( 5x )2 - y2
(2) (m+2n) (2n-m )
=4n2 -m2
= (2n)2 -m2
=(2n+m) (2n-m )
这里的( )相当于公式里的 a,( )相当于b
(a+b) (a-b)=a2-b2
(?+?) (?-?) =?2-?2
利用平方差公式计算,第一步先 明确是哪个数是a、哪个数是b ;第二步准确代入公式;第三步化简。
例1 用平方差公式计算:
(1) ( 5x + y ) ( 5x - y) (2) (m+2n) (2n-m )
典型例题
这里的( )相当于公式里的 a,( )相当于b
注意:①公式中的a与b可以是数也可以是单项式、多项式或其他代数式。
②正确判断哪个数为a,哪个数为b(与位置、自身的性质符号无关,两因式中的两对数是否有一个数完全相同,而另一个数是相反数)。
(a+b) (a-b)=a2-b2
(?+?) (?-?) =?2-?2
例2 计算:
(1) (3y - x ) (- x -3 y) (2) (m2 +n) (n-m2 )
解: (1) (3y - x ) (- x -3 y)
=x2 -9 y2
典型例题
= (- x )2 - (3y)2
(2) (m2 +n) (n-m2 )
=n2 –m4
=n2 - (m2) 2
=(n+m2) (n-m2 )
=(- x +3y) (- x -3 y)
这里的( )相当于公式里的 a,( )相当于b
(a+b) (a-b)=a2-b2
(?+?) (?-?) =?2-?2
例3 计算: 102×98
运用平方差公式可以起到简便运算的作用。
典型例题
解:(1) 102×98
=(100+2) × (100-2)
=1002-22
=10000-4
=9996
练一练:19×20
=(20 - )(20 )
=202 -()2
=400 -
=399
1.下面的计算是否正确?如有错误,请改正:
(1) (x+2) (x-2) =x2-2;
(2) (a+b) (b-a) =a2 -b2;
(3) (-3x+2) (3x-2) =9x2?4.
解: (1) 错误. 第二个数没有平方;
应改为: (x+2) (x-2) =x2-4;
(2) 错误. 公式中的a与b确认错误;
应改为: (a+b) (b-a) =b2 -a2;
(3) 错误. 这不是平方差公式,而是完全平方公式
应改为: (-3x+2) (3x-2) =-(3x-2) (3x-2) =-(3x-2) 2
= -(9x2?12x+4 )= -9x2+12x?4.
巩固练习
2.填空:
(1) (x+3) (x-3) = ;
(2) (+a) (a - ) = ;
(3) (x+ ) (x- ) =x2?36 ;
(4) (m+ ) (m- ) =m2?25n2 ;
(5) (a +b) ( ) =b2?a2 ;
(6) ( ) (1+x2) =x4?1.
巩固练习
3.如果(x+5) (x- a) = x2? b,则a = ,b= .
x2?9
a2 ?
6
6
5n
5n
b?a
x2?1
5
25
(a+b) (a-b)=a2-b2
4.用平方差公式计算:
(1) (1+x) (1-x); (2) (-a +3b) (-a -3b) ;
(3) (2a+3) (3-2a) ; (4) (x - 2y) (- x - 2y).
巩固练习
解: (1) (1+x ) (1-x)
=12 - x2
= 1 - x2
(3) (2a+3) (3-2a)
= 32- (2a)2
= 9 -4a2
(2) (-a +3b) (-a -3b)
= (-a) 2 - (3b)2
= a2 -9b2
(4) (x - 2y) (- x - 2y)
= (-2y )2 - ( x)2
=4y2 -x2
5. 计算:
(1) 49×51;
(2) (a +2) (a -2) -(a +5) (a -1) ;
(3) (x +3)2 +(x +1) (x -1).
拓展练习
解: (1) 49×51
=(50-1 ) (50+1)
= 502 - 12
=2500 – 1
=2499
(3) (x +3)2 +(x +1) (x -1)
= x2 +6x+9+ x2- 1
= 2x2 +6x+8
(2) (a +2) (a -2) -(a +5) (a -1)
=a2 – 22 – (a2 – a+5a –5 )
= a2 – 4 – a2 + a–5a +5
= –4a+1
课堂小结
平方差公式 (a+b) (a-b)=a2-b2
①熟记公式,弄清公式的特征
②关键是如何判断a、b
完全平方公式
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
乘法公式
再见
乘法公式(2)
学习目标
能推导平方差公式,了解公式的几何背景,并能利用公式进行简单计算;
经历探索平方差公式的过程,进一步感悟数与形的关系,感悟数形结合的思想。
完全平方公式:
(a b)2=a2 +b2
(a b)2=a2 +b2
公式再现
计算:(a+b+c)2
2ab
2ab
+
+
-
-
( a + b )2= a2 + 2 a b + b2
( + )2 = 2 + 2· · + 2
?
?
?
?
?
?
c
c
c
a+b
a+b
a+b
= [(a+b) +c]2
= a2+2ab+b2+2ac+2bc+c2
= (a+b)2+2·(a+b)·c+c2
= a2+b2+c2+2ab+2bc+2ac
计算:(a+b+c)2
(a+b+c)2=(a+b+c)(a+b+c)
= a2+b2+c2+2ab+2bc+2ac
代数方法:多项式×多项式
= a2+ab+ac
+ab+b2+bc
+ac+bc+c2
面积法:
通过图形的拼合
a
b
c
c
b
a
=
制作若干张长方形和正方形硬纸片,通过图形计算(a+b+c)2.
数学实验室
(a+b+c)2
a2+b2+c2+2ab+2bc+2ac
a2+ab+ac
+ab+b2+bc
+ac+bc+c2
a
b
c
c
b
a
完全平方公式:(a b)2=a2 +b2
(a b)2=a2 +b2
公式再现
2ab
2ab
+
+
-
-
(a+b+c)2= a2+b2+c2+2ab+2bc+2ac
练习:(m+n-t)2
=m2+n2+t2+2mn-2mt-2nt
计算 (1) (x+y) (x-y)
(2) (a+1) (a-1)
(3) (mn+a) (mn-a)
练一练
(x+y) (x-y) =x2﹣y2
(a+1) (a-1) =a2﹣1
(mn+a) (mn-a) =m2n2 ﹣a2
=x2 ﹣xy +xy - y2
=x2﹣y2
=a2﹣a +a - 1
=a2﹣1
= m2n2 ﹣mna +mna - a2
=m2n2﹣a2
一块边长为a米的正方形实验田,
a
因需要将在实验田一角挖一个边长为 b 米的正方形蓄水池,
形成如图所示实验田。
你能计算出此时实验田的面积吗?
a
b
b
法一
直
接
求
总面积=
法二
间
接
求
总面积=
(a+b) (a-b)=a2-b2
你发现了什么?
探索:
a2
- b2
创设情境
(a-b)
(a+b)
a-b
b
a-b
a
你还有其他方法计算实验田的面积吗?
a
b
b
法一
直
接
求
总面积=
法二
间
接
求
总面积=
a2
﹣b2
创设情境
a-b
a-b
(a+b) (a-b)=a2-b2
(a+b) (a-b) =a2 - b2
(a+b) (a-b) =
推证 ?
a2-ab+
ab-b2
= a2
- b2
上面的等式是利用面积的不同表示形式得到的,你还有其他方法吗?
探索
左边是:
的积;
右边是:
两个数和与
a
a
两个数的平方差
几
何
背景
两个数的和与这两个数的差的积等于这两个数的平方差.
两个数差
b
b
(a+b)(a?b)/2
(a+b) (a?b)
= a2?b2
初识 平方差公式
(a+b) (a-b) =a2 - b2
(a+b)(a?b)/2
说说这个公式的特点:
文字表述:
用自己的语言叙述上面的公式
平方差公式
(a+b) (a-b)=a2-b2
公式的文字表述:
两个数的和与这两个数的差的积等于这两个数的平方差.
新知
(y+5) (-y-5)
(5-y) (5+y)
?
?
(a+b) (a-b)=a2-b2
(?+?) (?-?) =?2-?2
( + ) ( - )
下列各式具有可以利用平方差公式计算的特征吗?
(1) (x+2y) (2x-y)
(2) (m-n) (n+m)
(3) (c+d) (-d-c)
(4) (2a+b) (2a-c)
辩一辩
( + ) ( - )
利用平方差公式计算,第一步先 明确是哪个数是a、哪个数是b ;第二步准确代入公式;第三步化简。
例1 用平方差公式计算:
(1) ( 5x + y ) ( 5x - y) (2) (m+2n) (2n-m )
解: (1) ( 5x + y ) ( 5x - y)
=25x2 - y2
典型例题
= ( 5x )2 - y2
(2) (m+2n) (2n-m )
=4n2 -m2
= (2n)2 -m2
=(2n+m) (2n-m )
这里的( )相当于公式里的 a,( )相当于b
(a+b) (a-b)=a2-b2
(?+?) (?-?) =?2-?2
利用平方差公式计算,第一步先 明确是哪个数是a、哪个数是b ;第二步准确代入公式;第三步化简。
例1 用平方差公式计算:
(1) ( 5x + y ) ( 5x - y) (2) (m+2n) (2n-m )
典型例题
这里的( )相当于公式里的 a,( )相当于b
注意:①公式中的a与b可以是数也可以是单项式、多项式或其他代数式。
②正确判断哪个数为a,哪个数为b(与位置、自身的性质符号无关,两因式中的两对数是否有一个数完全相同,而另一个数是相反数)。
(a+b) (a-b)=a2-b2
(?+?) (?-?) =?2-?2
例2 计算:
(1) (3y - x ) (- x -3 y) (2) (m2 +n) (n-m2 )
解: (1) (3y - x ) (- x -3 y)
=x2 -9 y2
典型例题
= (- x )2 - (3y)2
(2) (m2 +n) (n-m2 )
=n2 –m4
=n2 - (m2) 2
=(n+m2) (n-m2 )
=(- x +3y) (- x -3 y)
这里的( )相当于公式里的 a,( )相当于b
(a+b) (a-b)=a2-b2
(?+?) (?-?) =?2-?2
例3 计算: 102×98
运用平方差公式可以起到简便运算的作用。
典型例题
解:(1) 102×98
=(100+2) × (100-2)
=1002-22
=10000-4
=9996
练一练:19×20
=(20 - )(20 )
=202 -()2
=400 -
=399
1.下面的计算是否正确?如有错误,请改正:
(1) (x+2) (x-2) =x2-2;
(2) (a+b) (b-a) =a2 -b2;
(3) (-3x+2) (3x-2) =9x2?4.
解: (1) 错误. 第二个数没有平方;
应改为: (x+2) (x-2) =x2-4;
(2) 错误. 公式中的a与b确认错误;
应改为: (a+b) (b-a) =b2 -a2;
(3) 错误. 这不是平方差公式,而是完全平方公式
应改为: (-3x+2) (3x-2) =-(3x-2) (3x-2) =-(3x-2) 2
= -(9x2?12x+4 )= -9x2+12x?4.
巩固练习
2.填空:
(1) (x+3) (x-3) = ;
(2) (+a) (a - ) = ;
(3) (x+ ) (x- ) =x2?36 ;
(4) (m+ ) (m- ) =m2?25n2 ;
(5) (a +b) ( ) =b2?a2 ;
(6) ( ) (1+x2) =x4?1.
巩固练习
3.如果(x+5) (x- a) = x2? b,则a = ,b= .
x2?9
a2 ?
6
6
5n
5n
b?a
x2?1
5
25
(a+b) (a-b)=a2-b2
4.用平方差公式计算:
(1) (1+x) (1-x); (2) (-a +3b) (-a -3b) ;
(3) (2a+3) (3-2a) ; (4) (x - 2y) (- x - 2y).
巩固练习
解: (1) (1+x ) (1-x)
=12 - x2
= 1 - x2
(3) (2a+3) (3-2a)
= 32- (2a)2
= 9 -4a2
(2) (-a +3b) (-a -3b)
= (-a) 2 - (3b)2
= a2 -9b2
(4) (x - 2y) (- x - 2y)
= (-2y )2 - ( x)2
=4y2 -x2
5. 计算:
(1) 49×51;
(2) (a +2) (a -2) -(a +5) (a -1) ;
(3) (x +3)2 +(x +1) (x -1).
拓展练习
解: (1) 49×51
=(50-1 ) (50+1)
= 502 - 12
=2500 – 1
=2499
(3) (x +3)2 +(x +1) (x -1)
= x2 +6x+9+ x2- 1
= 2x2 +6x+8
(2) (a +2) (a -2) -(a +5) (a -1)
=a2 – 22 – (a2 – a+5a –5 )
= a2 – 4 – a2 + a–5a +5
= –4a+1
课堂小结
平方差公式 (a+b) (a-b)=a2-b2
①熟记公式,弄清公式的特征
②关键是如何判断a、b
完全平方公式
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
乘法公式
再见
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
