人教版七年级数学下册9.1.2不等式的性质 (3)(共33张PPT)
文档属性
| 名称 | 人教版七年级数学下册9.1.2不等式的性质 (3)(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 00:00:00 | ||
图片预览







文档简介
(共33张PPT)
不等式的性质
用“<”或“>”填空,并找一找其中的规律.
(2)-1<3 , -1+2____3+2 , -1-3____3-3 ;
(1)5>3, 5+2____3+2 , 5-2____3-2 ;
不等式两边加(或减)同一个数 (或式子),不等号的方向______.
不变
>
>
<
<
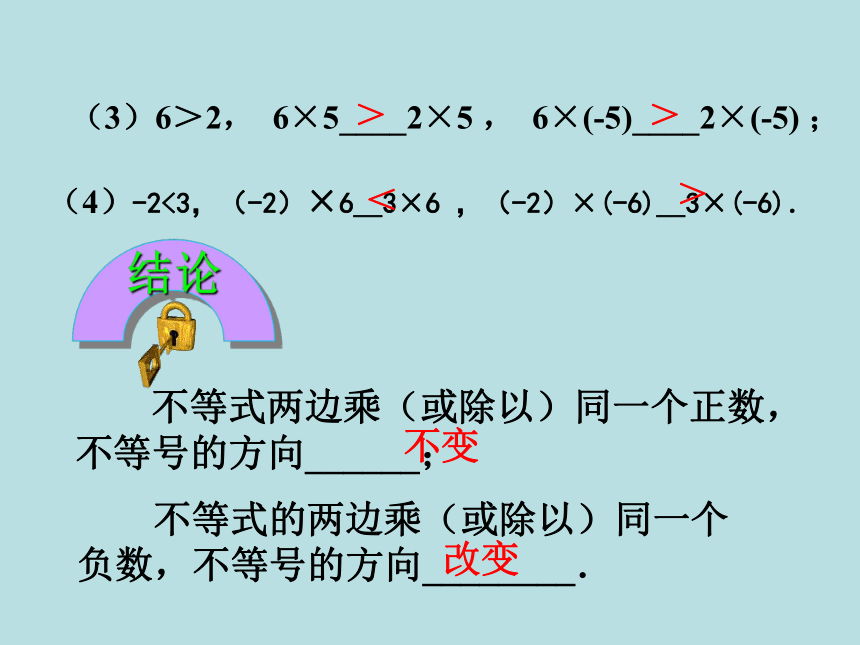
不等式的两边乘(或除以)同一个负数,不等号的方向________.
(3)6>2, 6×5____2×5 , 6×(-5)____2×(-5) ;
(4)-2<3,(-2)×6__3×6 ,(-2)×(-6)__3×(-6).
不等式两边乘(或除以)同一个正数,不等号的方向______;
不变
改变
>
>
>
<
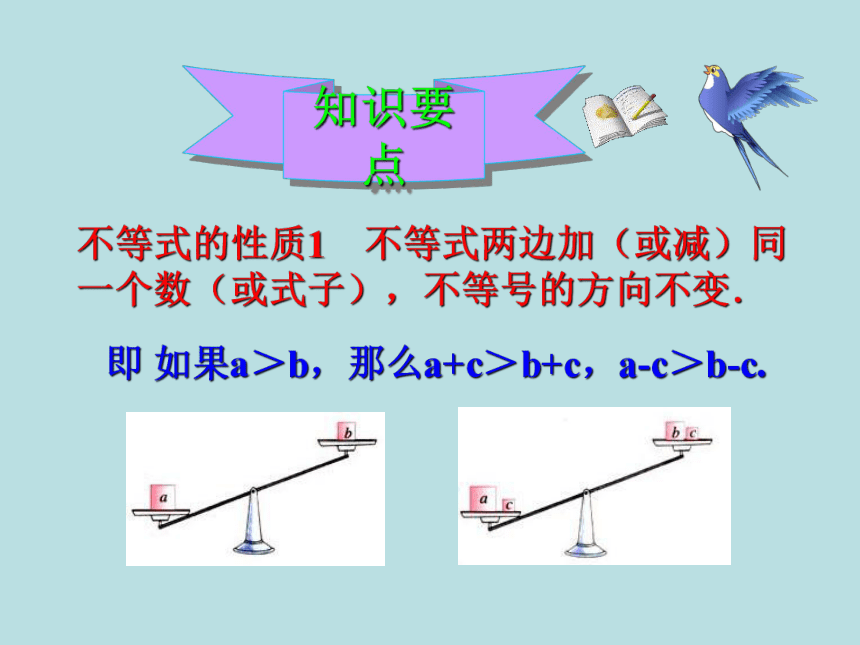
不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变.
即 如果a>b,那么a+c>b+c,a-c>b-c.
知识要点
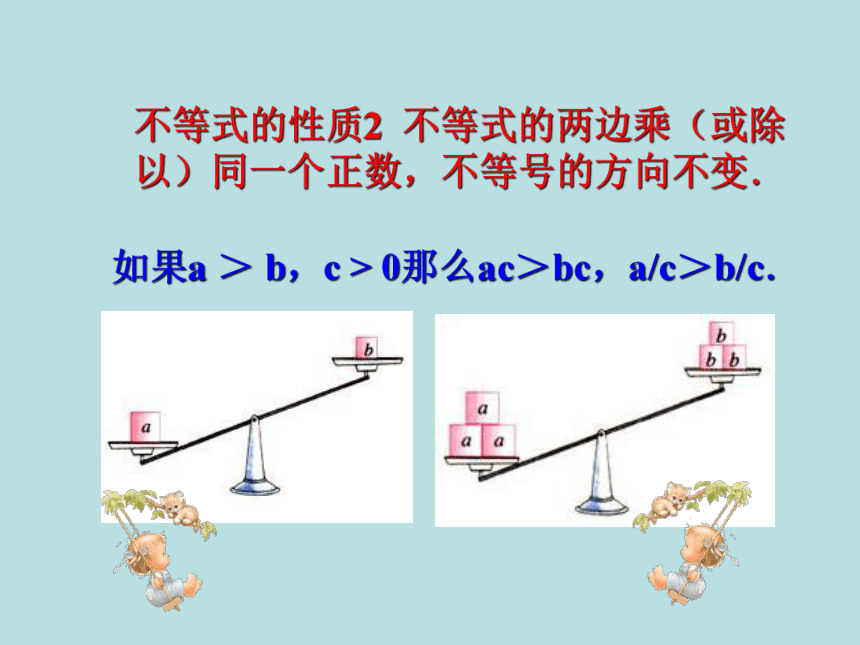
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a > b,c > 0那么ac>bc,a/c>b/c.
不等式的性质3 不等式两边乘(或除以)
同一个负数,不等号的方向改变.
如果 a > b ,c < 0 那么 ac < bc,a/c < b/c.
如果a>b,且c>d,那么a+c>b+d .
如果a>b,那么bb .
如果a>b,且b>c,那么a>c.
不等式的对称性:
不等式的传递性:
课堂检测:
1、若a>b,用“<”或“>”填空。
(1)a+1 b+1; (2) a-5 b-5; (3) -3a -3b; (4) 6-a 6-b;
小试牛刀
(1)3a 3b;
(2)a-8 b-8
(3)-2a -2b
(4)2a-5 2b-5
(5)-3.5a+1 -3.5b+1
设a>b,用“>”或“<”填空:
>
>
<
>
<
2.判断正误:
(1)∵a+8>4 ∴a>-4 ( )
(2)∵3>2 ∴3a>2a( )
(3)∵-1>-2 ∴a-1>a-2 ( )
(4)∵ab>0 ∴a>0,b> 0( )
×
×
√
√
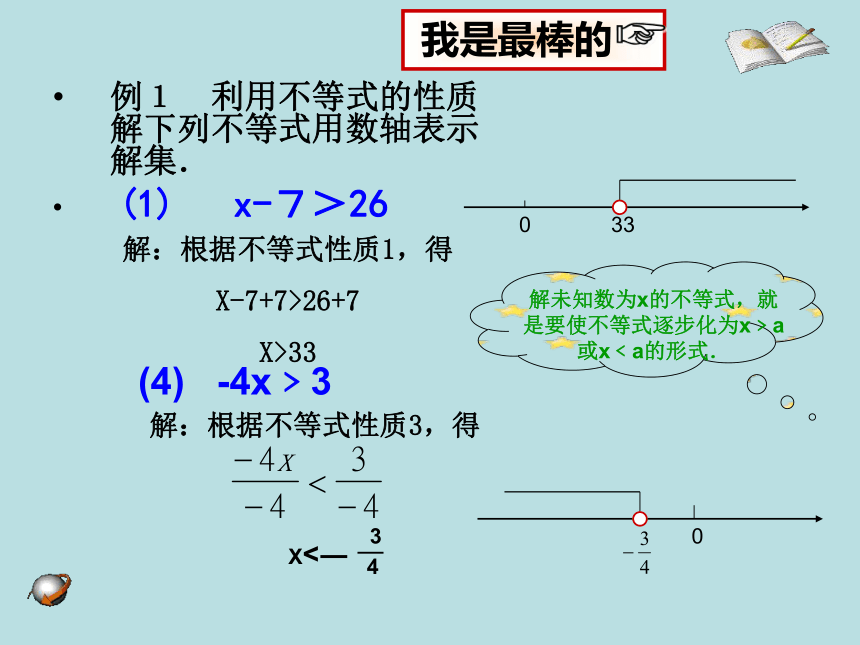
例1 利用不等式的性质解下列不等式用数轴表示解集.
(1) x-7>26
解:根据不等式性质1,得
X-7+7>26+7
X>33
(4) -4x﹥3
解:根据不等式性质3,得
(2) 3x<2x+1
3x-2x﹤2x+1-2x x﹤1
这个不等式的解在数轴上的表示
注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.
解:根据不等式性质1,得
3x-2x﹤1
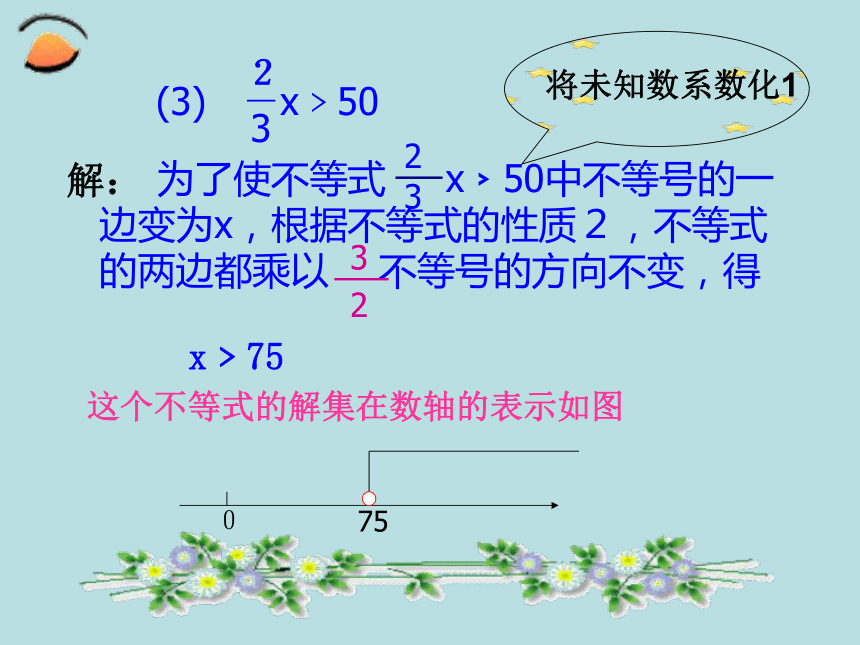
x﹥75
这个不等式的解集在数轴的表示如图
解:
例1 某长方体形状的容器长5cm,宽3cm,
高10cm。容器内原有水的高度为3cm,
现准备向它继续注水。用V(单位: )
表示新注入水的体积,写出V的取值范围。
解:新注入水的体积V与原有水的体积的和不能
超过容器的容积,即
V+3×5×3≤3×5×10
解得 V≤105
又由于新注入水的体积不能是负数,因此,
V的取值范围是
V≥0并且V≤105
在数轴上表示V的取值范围如图
0
105
课堂练习
课本第119练习题1,2
例2 已知a<0 ,试比较2a与a的大小.
解法一:∵2>1,a<0,
∴2a<a(不等式的性质3)
解法二: 在数轴上分别表示2a和a的点(a<0),如图:2a位于a的左边,所以2a<a.
解法三:∵ 2a-a=a, 又∵ a<0,
∴ 2a-a<0,
∴2a 例3 放鞭炮时,如果导火索燃烧的速度是0.8 cm/s,人跑开的速度是每秒4m,为了使点导火索的人在鞭炮燃放时跑到100 m以外的安全区域,这个导火索的长度应大于多少㎝?
解:设导火索的长度是x cm .根据题意,得
答:导火索的长度应大于20 cm.
解得: x≥20
例4 试证明三角形中任意两边之差小于第三边.
三角形中任意两边之差小于第三边.
证明:如图,设a,b,c为任意一个三角形的三条边的长,则
a+b>c, b+c>a, c+a>b.
由式子a+b>c 移项可得
a>c-b, b>c-a .
类似地,由式子b+c>a及c+a>b移项可得
c>a-b, b>a-c 及 c>b-a, a>b-c
例5 我国于2001年12月11日正式加入世界贸易组织(WTO).加入前,产品A的进口税超过产品B的进口税的1倍以上;加入后,这两种产品的进口税都下调了15%.你认为加入后产品A的进口税仍超过产品B的进口税的1倍以上吗?请说明理由.
解:设加入前产品A,B的进口税分别为a,b.由题意,得
a>2b.
加入后A,B两种产品的进口税分别为:
(1-15%)a,(1-15%)b,
∵ 1-15%>0
∴(1-15%)a>2 (1-15%)b
由不等式的基本性质3,
即表示产品A的进口税仍超过产品B的进口税的1倍以上.
解:不等式x+3 <7的两边都减去3,得:
x+3 -3<7-3
∴x<4
而满足x<3的正整数有1,2,3,
所以不等式的正整数解为1,2,3.
例6 求不等式x+3<7的正整数解.
解一元一次不等式的一般步骤:
(1)去分母:各项都乘以分母的最小公倍数;
(2)去括号:注意符号问题;
(3)移项:移项要变号;
(4)合并同类项:系数相加,字母及字母的指
数不变;
(5)系数化为1:不等式两边同除以未知数的系
数.(或同乘以未知数系数的倒数)
解 :去分母,得
去括号,得
移项、得
合并同类项,得
两边都除以5,得
3(x-3) ≥2(8-x)
3x-9≥16-2x
3x+2x≥16+9
5x≥25
x≥5
解:
移项得:
5x-4x>-4-10
合并得
x>-14
例8 解不等式 5(x+2)>4x-4.
去括号得:
5x+10>4x-4
解:
移项得:
2x-3x<-9-6
合并得:
-x<-15
例9 解不等式 2(x+3)<3(x-3).
去括号得:
2x+6<3x-9
x>15
系数化为1得:
解:去分母,得
3(2x+1) <2(13x-2) -4(6x+4)
去括号,得
6x+3<26x-4-24x-16
移项,得
6x-26x+24x<-4-16-3
合并,得
4x<-23
一元一次不等式ax>b和ax(其中a、b都是已知数)的解集是
条件
解集
类型
a>0 a=0
a<0
b>0 b=0 b>0
ax>b {x︱x>b/a} 空集 空集 R {x︱xaxb/a}
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
在(1)与(5)这两步若乘以(或除以)负数,要把不等号方向改变
两边同时除以未知数的系数
一般只有一个解
一般解集含有无数个解
一元一次方程与一元一次不等式的解法步骤比较
一元一次方程 一元一次不等式
解法步骤
解的情况
不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.
解一元一次不等式的一般步骤:
(1)去分母:各项都乘以分母的最小公倍数;
(2)去括号:注意符号问题;
(3)移项:移项要变号;
(4)合并同类项:系数相加,字母及字母的指数不变;
(5)系数化为1:不等式两边同除以未知数的系数.(或同乘以未知数系数的倒数)
>
>
<
5 >1
x≥2
7. 解不等式3-x<2x+6并把它的解集表示在
数轴上.
解:两边都加上x,得 3<2x+6+x
合并同类项,得 3<3x+6
两边都减去6,得 3-6<3x+6-6
合并同类项,得 -3<3x
两边都除以3,得 -1即 x>-1
这个不等式的解集在数轴上表示如下图:
8. m取何值时,关于x的方程
解:解这个方程
根据题意,得
解得 m>1
9.如果不等式3x-m≤0的正整数解是1、2、3,
则m的取值范围是__________.
分析:不等式3x-m≤0的解为:x≤
可得: 3 ≤ <4
9≤m<12
不等式的性质
用“<”或“>”填空,并找一找其中的规律.
(2)-1<3 , -1+2____3+2 , -1-3____3-3 ;
(1)5>3, 5+2____3+2 , 5-2____3-2 ;
不等式两边加(或减)同一个数 (或式子),不等号的方向______.
不变
>
>
<
<
不等式的两边乘(或除以)同一个负数,不等号的方向________.
(3)6>2, 6×5____2×5 , 6×(-5)____2×(-5) ;
(4)-2<3,(-2)×6__3×6 ,(-2)×(-6)__3×(-6).
不等式两边乘(或除以)同一个正数,不等号的方向______;
不变
改变
>
>
>
<
不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变.
即 如果a>b,那么a+c>b+c,a-c>b-c.
知识要点
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a > b,c > 0那么ac>bc,a/c>b/c.
不等式的性质3 不等式两边乘(或除以)
同一个负数,不等号的方向改变.
如果 a > b ,c < 0 那么 ac < bc,a/c < b/c.
如果a>b,且c>d,那么a+c>b+d .
如果a>b,那么b
如果a>b,且b>c,那么a>c.
不等式的对称性:
不等式的传递性:
课堂检测:
1、若a>b,用“<”或“>”填空。
(1)a+1 b+1; (2) a-5 b-5; (3) -3a -3b; (4) 6-a 6-b;
小试牛刀
(1)3a 3b;
(2)a-8 b-8
(3)-2a -2b
(4)2a-5 2b-5
(5)-3.5a+1 -3.5b+1
设a>b,用“>”或“<”填空:
>
>
<
>
<
2.判断正误:
(1)∵a+8>4 ∴a>-4 ( )
(2)∵3>2 ∴3a>2a( )
(3)∵-1>-2 ∴a-1>a-2 ( )
(4)∵ab>0 ∴a>0,b> 0( )
×
×
√
√
例1 利用不等式的性质解下列不等式用数轴表示解集.
(1) x-7>26
解:根据不等式性质1,得
X-7+7>26+7
X>33
(4) -4x﹥3
解:根据不等式性质3,得
(2) 3x<2x+1
3x-2x﹤2x+1-2x x﹤1
这个不等式的解在数轴上的表示
注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.
解:根据不等式性质1,得
3x-2x﹤1
x﹥75
这个不等式的解集在数轴的表示如图
解:
例1 某长方体形状的容器长5cm,宽3cm,
高10cm。容器内原有水的高度为3cm,
现准备向它继续注水。用V(单位: )
表示新注入水的体积,写出V的取值范围。
解:新注入水的体积V与原有水的体积的和不能
超过容器的容积,即
V+3×5×3≤3×5×10
解得 V≤105
又由于新注入水的体积不能是负数,因此,
V的取值范围是
V≥0并且V≤105
在数轴上表示V的取值范围如图
0
105
课堂练习
课本第119练习题1,2
例2 已知a<0 ,试比较2a与a的大小.
解法一:∵2>1,a<0,
∴2a<a(不等式的性质3)
解法二: 在数轴上分别表示2a和a的点(a<0),如图:2a位于a的左边,所以2a<a.
解法三:∵ 2a-a=a, 又∵ a<0,
∴ 2a-a<0,
∴2a
解:设导火索的长度是x cm .根据题意,得
答:导火索的长度应大于20 cm.
解得: x≥20
例4 试证明三角形中任意两边之差小于第三边.
三角形中任意两边之差小于第三边.
证明:如图,设a,b,c为任意一个三角形的三条边的长,则
a+b>c, b+c>a, c+a>b.
由式子a+b>c 移项可得
a>c-b, b>c-a .
类似地,由式子b+c>a及c+a>b移项可得
c>a-b, b>a-c 及 c>b-a, a>b-c
例5 我国于2001年12月11日正式加入世界贸易组织(WTO).加入前,产品A的进口税超过产品B的进口税的1倍以上;加入后,这两种产品的进口税都下调了15%.你认为加入后产品A的进口税仍超过产品B的进口税的1倍以上吗?请说明理由.
解:设加入前产品A,B的进口税分别为a,b.由题意,得
a>2b.
加入后A,B两种产品的进口税分别为:
(1-15%)a,(1-15%)b,
∵ 1-15%>0
∴(1-15%)a>2 (1-15%)b
由不等式的基本性质3,
即表示产品A的进口税仍超过产品B的进口税的1倍以上.
解:不等式x+3 <7的两边都减去3,得:
x+3 -3<7-3
∴x<4
而满足x<3的正整数有1,2,3,
所以不等式的正整数解为1,2,3.
例6 求不等式x+3<7的正整数解.
解一元一次不等式的一般步骤:
(1)去分母:各项都乘以分母的最小公倍数;
(2)去括号:注意符号问题;
(3)移项:移项要变号;
(4)合并同类项:系数相加,字母及字母的指
数不变;
(5)系数化为1:不等式两边同除以未知数的系
数.(或同乘以未知数系数的倒数)
解 :去分母,得
去括号,得
移项、得
合并同类项,得
两边都除以5,得
3(x-3) ≥2(8-x)
3x-9≥16-2x
3x+2x≥16+9
5x≥25
x≥5
解:
移项得:
5x-4x>-4-10
合并得
x>-14
例8 解不等式 5(x+2)>4x-4.
去括号得:
5x+10>4x-4
解:
移项得:
2x-3x<-9-6
合并得:
-x<-15
例9 解不等式 2(x+3)<3(x-3).
去括号得:
2x+6<3x-9
x>15
系数化为1得:
解:去分母,得
3(2x+1) <2(13x-2) -4(6x+4)
去括号,得
6x+3<26x-4-24x-16
移项,得
6x-26x+24x<-4-16-3
合并,得
4x<-23
一元一次不等式ax>b和ax
条件
解集
类型
a>0 a=0
a<0
b>0 b=0 b>0
ax>b {x︱x>b/a} 空集 空集 R {x︱xaxb/a}
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1
在(1)与(5)这两步若乘以(或除以)负数,要把不等号方向改变
两边同时除以未知数的系数
一般只有一个解
一般解集含有无数个解
一元一次方程与一元一次不等式的解法步骤比较
一元一次方程 一元一次不等式
解法步骤
解的情况
不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.
解一元一次不等式的一般步骤:
(1)去分母:各项都乘以分母的最小公倍数;
(2)去括号:注意符号问题;
(3)移项:移项要变号;
(4)合并同类项:系数相加,字母及字母的指数不变;
(5)系数化为1:不等式两边同除以未知数的系数.(或同乘以未知数系数的倒数)
>
>
<
5 >1
x≥2
7. 解不等式3-x<2x+6并把它的解集表示在
数轴上.
解:两边都加上x,得 3<2x+6+x
合并同类项,得 3<3x+6
两边都减去6,得 3-6<3x+6-6
合并同类项,得 -3<3x
两边都除以3,得 -1
这个不等式的解集在数轴上表示如下图:
8. m取何值时,关于x的方程
解:解这个方程
根据题意,得
解得 m>1
9.如果不等式3x-m≤0的正整数解是1、2、3,
则m的取值范围是__________.
分析:不等式3x-m≤0的解为:x≤
可得: 3 ≤ <4
9≤m<12
