人教版八年级数学下册18.1.2平行四边形的判定(第二课时)---三角形中位线课件(共19张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.1.2平行四边形的判定(第二课时)---三角形中位线课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 198.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 13:28:52 | ||
图片预览




文档简介
(共19张PPT)
人教版八年级数学
第十八章 平行四边形
18.1.2平行四边形的判定(第二课时)
------------三角形中位线
课标解读
1.理解三角形中位线的概念,能够运用平行四边形的知识得出三角形中位线的性质定理
2.掌握三角形中位线定理,并能灵活运用这个定理解决问题。
3.通过探索三角形中位线的性质,进一步培养识图能力和推理论证能力。
知识梳理
1.三角形的中位线的概念
连接三角形两边中点的线段叫做三角形的中位线
温馨提示;任意一个三角形都有三条中位线。
B
A
F
E
D
C
2.三角形的中位线定理
内容:三角形的中位线平行于第三边,并且等于第三边的一半。
推理格式:∵DE分别是AB,AC的中点,
∴DE//BC, DE= BC
A
E
D
C
B
作用:(1)位置关系:可以证明两条直线平行
(2)数量关系:可以证明线段的相等或倍分
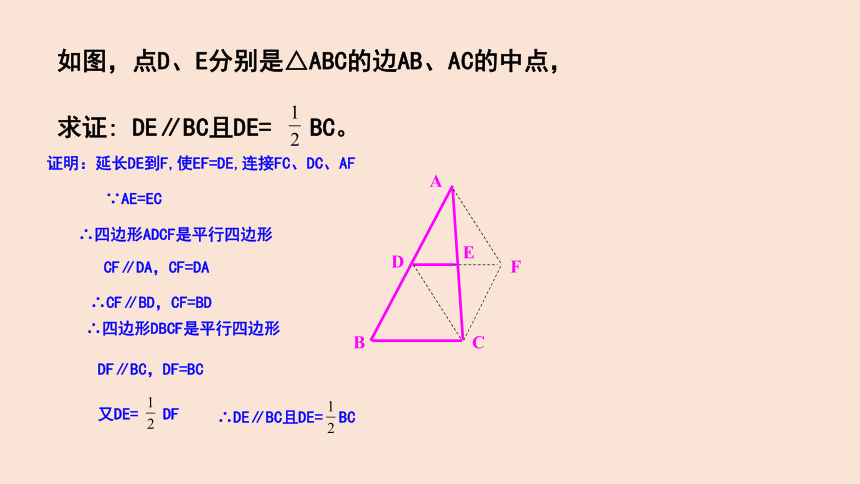
如图,点D、E分别是△ABC的边AB、AC的中点,
求证: DE∥BC且DE= BC。
B
C
A
D
E
F
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC
CF∥DA,CF=DA
∴CF∥BD,CF=BD
DF∥BC,DF=BC
又DE= DF
∴DE∥BC且DE= BC
题型一:一条中位线的问题
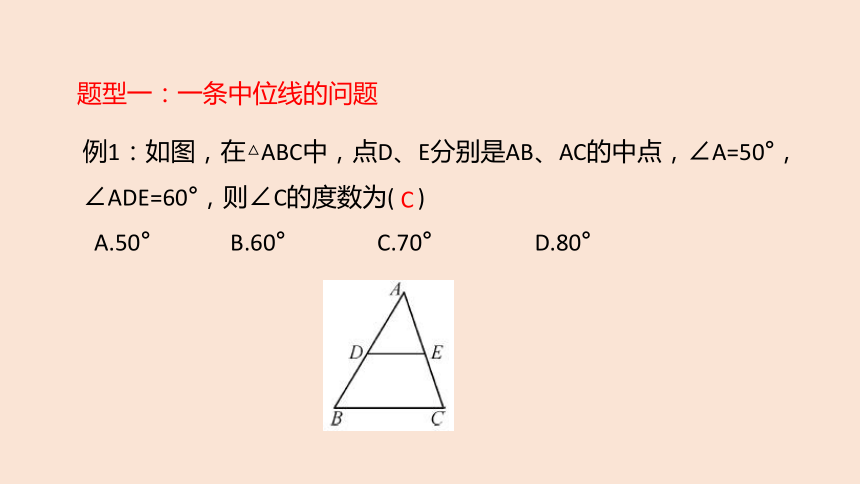
例1:如图,在△ABC中,点D、E分别是AB、AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
C
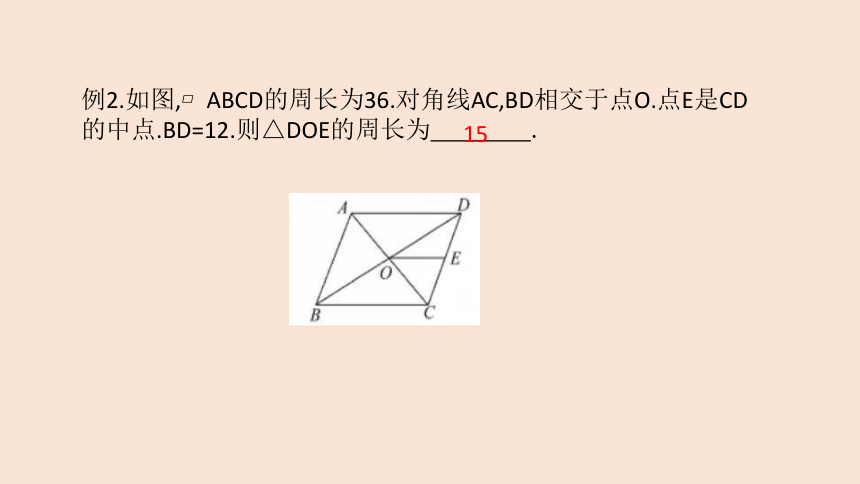
例2.如图,?ABCD的周长为36.对角线AC,BD相交于点O.点E是CD的中点.BD=12.则△DOE的周长为 .
15
【解析】∵?ABCD的周长为36,
∴BC+CD=18. ∵四边形ABCD为平行四边形, ∴O是BD的中点,∴OD=6, 又∵E是CD的中点, ∴OE是△BCD的中位线, ∴OE=
DE=
∴OE+DE=9, ∴△DOE的周长=OD+OE+DE=6+9=15
BC,
CD
1.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( ) A.20 B.12 C.14 D.13
C
同步练习
2.如图,EF是△ABC的中位线,BD平分∠ABC交EF于点D,若DE=2,则EB=__________.
2
题型二:多条中位线的问题
AC.
例3.已知如图,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连接AC.
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴HG∥AC,HG=
同理可得:EF∥AC,EF=
AC
∴HG∥EF且HG=EF.∴四边形EFGH是平行四边形.
1.已知,如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
温馨提示:连接AC.利用三角形中位线,得EH//FG,EH=FG,再利用一组对边平行且相等得到平行四边形
同步练习
2.如图,D 是△ABC 内一点,BD⊥CD,AD=7,BD=4,CD=3,E,F,G,H分别是 AB,BD,CD,AC 的中点,则四边形 EFGH 的周长为( )
A.12 B.14 C.24 D.21
A
题型三:与中位线定理有关的辅助线作法
(1)如果有中线可将中线延长一倍. (2)如果有线段倍分问题时可考虑作中位线. (3)如果有中点,可在同一三角形一边上取中点,作中位线,或构造一个三角形,使图形中的线段为所构造三角形的中位线.
例4.如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,求EF的长
∵AB∥CD,
∴∠C=∠A,∠CDE=∠AHE.
∵E是AC的中点,
∴AE=EC,
∴△DCE≌△HAE.
∴DE=HE,DC=AH=3.
∵F是BD的中点,
∴EF是三角形DHB的中位线
∴EF=
解:连接DE并延长交AB于H.
又∵BH=AB-AH=5-3=2 ∴EF=1.
BH
1.如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为 .
1
拓展提升
2.如图所示,在四边形ABCD中,P为对角线BD的中点,E,F分别为AB,CD的 中点,AD=BC,∠PEF=18°,则∠PFE的度数是 .
18°
3.如图,△ABC的周长是32,以它的三边中点为顶点组成第2个三角形,再以第2 个三角形的三边中点为顶点组成第3个三角形,…,则第n个三角形的周长为 .
26-n
人教版八年级数学
第十八章 平行四边形
18.1.2平行四边形的判定(第二课时)
------------三角形中位线
课标解读
1.理解三角形中位线的概念,能够运用平行四边形的知识得出三角形中位线的性质定理
2.掌握三角形中位线定理,并能灵活运用这个定理解决问题。
3.通过探索三角形中位线的性质,进一步培养识图能力和推理论证能力。
知识梳理
1.三角形的中位线的概念
连接三角形两边中点的线段叫做三角形的中位线
温馨提示;任意一个三角形都有三条中位线。
B
A
F
E
D
C
2.三角形的中位线定理
内容:三角形的中位线平行于第三边,并且等于第三边的一半。
推理格式:∵DE分别是AB,AC的中点,
∴DE//BC, DE= BC
A
E
D
C
B
作用:(1)位置关系:可以证明两条直线平行
(2)数量关系:可以证明线段的相等或倍分
如图,点D、E分别是△ABC的边AB、AC的中点,
求证: DE∥BC且DE= BC。
B
C
A
D
E
F
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∴四边形ADCF是平行四边形
∴四边形DBCF是平行四边形
∵AE=EC
CF∥DA,CF=DA
∴CF∥BD,CF=BD
DF∥BC,DF=BC
又DE= DF
∴DE∥BC且DE= BC
题型一:一条中位线的问题
例1:如图,在△ABC中,点D、E分别是AB、AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
C
例2.如图,?ABCD的周长为36.对角线AC,BD相交于点O.点E是CD的中点.BD=12.则△DOE的周长为 .
15
【解析】∵?ABCD的周长为36,
∴BC+CD=18. ∵四边形ABCD为平行四边形, ∴O是BD的中点,∴OD=6, 又∵E是CD的中点, ∴OE是△BCD的中位线, ∴OE=
DE=
∴OE+DE=9, ∴△DOE的周长=OD+OE+DE=6+9=15
BC,
CD
1.如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( ) A.20 B.12 C.14 D.13
C
同步练习
2.如图,EF是△ABC的中位线,BD平分∠ABC交EF于点D,若DE=2,则EB=__________.
2
题型二:多条中位线的问题
AC.
例3.已知如图,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连接AC.
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴HG∥AC,HG=
同理可得:EF∥AC,EF=
AC
∴HG∥EF且HG=EF.∴四边形EFGH是平行四边形.
1.已知,如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
温馨提示:连接AC.利用三角形中位线,得EH//FG,EH=FG,再利用一组对边平行且相等得到平行四边形
同步练习
2.如图,D 是△ABC 内一点,BD⊥CD,AD=7,BD=4,CD=3,E,F,G,H分别是 AB,BD,CD,AC 的中点,则四边形 EFGH 的周长为( )
A.12 B.14 C.24 D.21
A
题型三:与中位线定理有关的辅助线作法
(1)如果有中线可将中线延长一倍. (2)如果有线段倍分问题时可考虑作中位线. (3)如果有中点,可在同一三角形一边上取中点,作中位线,或构造一个三角形,使图形中的线段为所构造三角形的中位线.
例4.如图,AB∥CD,E,F分别为AC,BD的中点,若AB=5,CD=3,求EF的长
∵AB∥CD,
∴∠C=∠A,∠CDE=∠AHE.
∵E是AC的中点,
∴AE=EC,
∴△DCE≌△HAE.
∴DE=HE,DC=AH=3.
∵F是BD的中点,
∴EF是三角形DHB的中位线
∴EF=
解:连接DE并延长交AB于H.
又∵BH=AB-AH=5-3=2 ∴EF=1.
BH
1.如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为 .
1
拓展提升
2.如图所示,在四边形ABCD中,P为对角线BD的中点,E,F分别为AB,CD的 中点,AD=BC,∠PEF=18°,则∠PFE的度数是 .
18°
3.如图,△ABC的周长是32,以它的三边中点为顶点组成第2个三角形,再以第2 个三角形的三边中点为顶点组成第3个三角形,…,则第n个三角形的周长为 .
26-n
