鲁教版(五四制)山东省东平县实验中学2019-2020学年六年级下册数学第七章相交线与平行线质量检测(word版有答案)
文档属性
| 名称 | 鲁教版(五四制)山东省东平县实验中学2019-2020学年六年级下册数学第七章相交线与平行线质量检测(word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 251.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 13:02:36 | ||
图片预览


文档简介
东平县实验中学2019-2020学年六年级下册第七章相交线与平行线质量检测
(时间:60分钟 满分100分)
一、选择题(每小题3分,共36分)
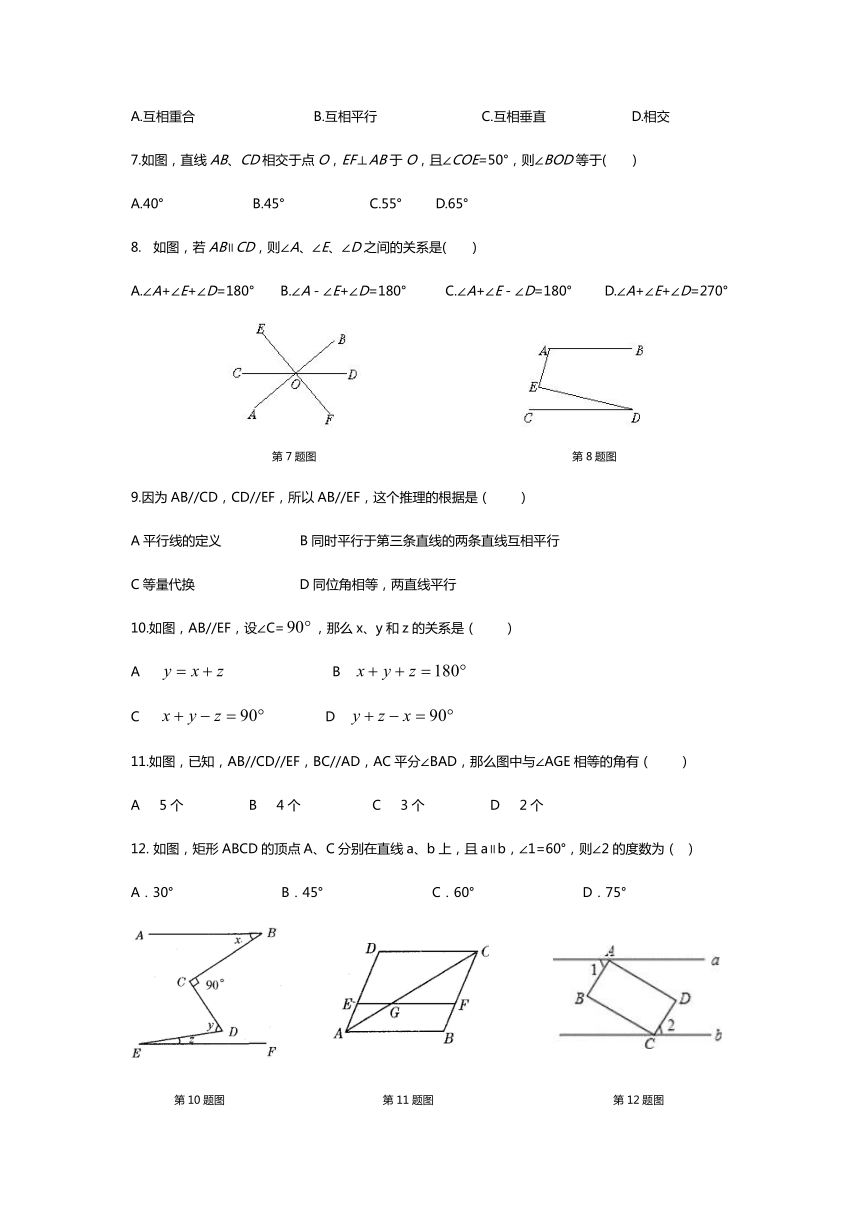
1.如图,下列四个条件中,能判定DE∥AC的是( )
A.∠3=∠4 B.∠1=∠2 C.∠EDC=∠EFC D.∠ACD=∠AFE
2.如图,AB∥CD,EF∥GH,∠1=60°,则∠2补角的度数是( )
第1题图 第2题图 第3题图
A.60° B.100° C.110° D.120°
3. 如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则
∠GHC等于( )
A.112° B.110° C.108° D.106°
4.下列图形中,由AB∥CD,能得到∠1=∠2的是( )
A. B.C. D.
5.一辆汽午在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
A.第一次右拐第二次左拐 B.第一次左拐,第二次右拐
C.第一次左拐第二次左拐 D.第一次右拐,第二次右拐
6.两平行直线被第三条直线所截,同位角的平分线( )
A.互相重合 B.互相平行 C.互相垂直 D.相交
7.如图,直线AB、CD相交于点O,EF⊥AB于O,且∠COE=50°,则∠BOD等于( )
A.40° B.45° C.55° D.65°
8. 如图,若AB∥CD,则∠A、∠E、∠D之间的关系是( )
A.∠A+∠E+∠D=180° B.∠A-∠E+∠D=180° C.∠A+∠E-∠D=180° D.∠A+∠E+∠D=270°
第7题图 第8题图
9.因为AB//CD,CD//EF,所以AB//EF,这个推理的根据是( )
A平行线的定义 B同时平行于第三条直线的两条直线互相平行
C等量代换 D同位角相等,两直线平行
10.如图,AB//EF,设∠C=,那么x、y和z的关系是( )
A B
C D
11.如图,已知,AB//CD//EF,BC//AD,AC平分∠BAD,那么图中与∠AGE相等的角有( )
A 5个 B 4个 C 3个 D 2个
12. 如图,矩形ABCD的顶点A、C分别在直线a、b上,且a∥b,∠1=60°,则∠2的度数为( )
A.30° B.45° C.60° D.75°
第10题图 第11题图 第12题图
2、选择题(每小题3分,共12分)
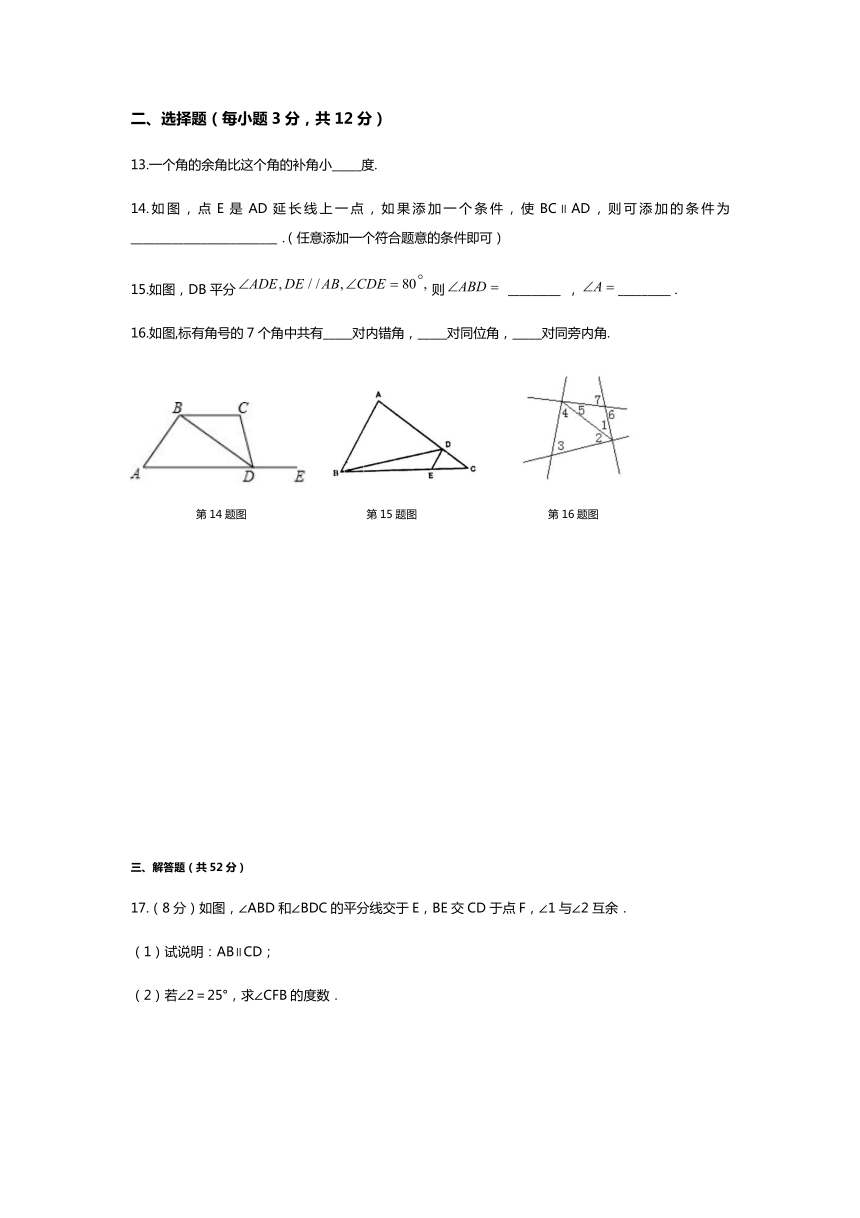
13.一个角的余角比这个角的补角小_____度.
14.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为_________________________.(任意添加一个符合题意的条件即可)
15.如图,DB平分则 _________ ,_________ .
16.如图,标有角号的7个角中共有_____对内错角,_____对同位角,_____对同旁内角.
第14题图 第15题图 第16题图
3、解答题(共52分)
17.(8分)如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1与∠2互余.
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠CFB的度数.
18.(12分)如图:完成下列推理过程.
①∵AB//CD(已知),∴∠ABC=__________( )____________=______________(两直线平行,内错角相等),∴∠BCD+____________=( )
②∵∠3=∠4(已知),∴____________∥____________( )
③∵∠FAD=∠FBC(已知),∴_____________∥____________( )
第18题图 第19题图
19.(10分)如图,AB//CD,BEFGD是折线,那么∠B+∠F+∠D=∠E+∠G吗?简述你的理由.
20.(10分)如图,已知AD⊥BC,EF⊥BC,∠4=∠C,那么∠1=∠2.谈谈你的理由.
21.(12分)已知E、D分别在∠AOB的边OA、OB上,C为平面内一点,DE、DF分别是∠CDO、∠CDB的平分线.
(1)如图1,若点C在OA上,且FD∥AO,求证:DE⊥AO;
(2)如图2,若点C在∠AOB的内部,且∠DEO=∠DEC,请猜想∠DCE、∠AEC、∠CDB之间的数量关系,并证明;
(3)若点C在∠AOB的外部,且∠DEO=∠DEC,请根据图3、图4分别写出∠DCE、∠AEC、∠CDB之间的数量关系(不需证明).
附:参考答案
1~12:ADDBB BACBC AC
13. 90
14. 略
15. 500 800
16. 4 2 4
17.解:(1)∵∠ABD和∠BDC的平分线交于E,BE交CD于点F,
∴∠ABD=2∠1,∠BDC=2∠2,
∵∠1与∠2互余,
∴∠1+∠2=90°,
∴∠ABD+∠BDC=180°,
∴AB∥CD;
(2)∵∠2=25°,∠1+∠2=90°,
∴∠1=65°,
∵∠ABD的角平分线是BF,
∴∠ABF=65°,
∵AB∥CD,
∴∠CFB=180°﹣∠ABF=180°﹣65°=115°.
18.①∠ABC=∠DCE,(两直线平行,同位角相等),∠1=∠2,∠BCD+∠ABC(两直线平行,同旁内角互补).
②AD∥BC,(内错角相等,两直线平行).
③AD∥BC,(同位角相等,两直线平行).
19.提示:过E、F、G作AB的平行线.
20.解:∵AD⊥BC(已知),EF⊥BC(已知),
∴AD∥EF(垂直于同一条直线的两直线平行),
∴∠1=∠3(两直线平行,同位角相等).
又∵∠4=∠C(已知).
∴AC∥GD(同位角相等,两直线平行).
∴∠2=∠3(两直线平行,内错角相等).
∴∠1=∠2(等量代换).
21.解:(1)如图1,∵DE、DF分别是∠CDO、∠CDB的平分线,
∴∠CDF=∠CDB,∠CDE=∠CDO,
∴∠EDF=(∠CDB+∠CDO)=90°,
又∵DF∥AO,
∴∠AED=90°,
∴DE⊥AO;
(2)如图2,连接OC,
∵∠DEO=∠DEC,∠EDO=∠EDC,
∴∠DOE=∠DCE,
∵∠CDB是△COD的外角,∠AEC是△COE的外角,
∴∠CDB=∠COD+∠OCD,∠AEC=∠EOC+∠ECO,
∴∠CDB+∠AEC=∠COD+∠OCD+∠EOC+∠ECO=2∠DCE;
(3)图3中,∠CDB=∠AEC+2∠DCE;图4中,∠AEC=∠CDB+2∠DCE.理由:
如图3,∵∠DEO=∠DEC,∠EDO=∠EDC,
∴∠DOE=∠DCE,
∵∠CDB是△ODG的外角,
∴∠CDB=∠DOG+∠DGO,
∵∠DGO是△CEG的外角,
∴∠DGO=∠AEC+∠C,
∴∠CDB=∠DOG+∠AEC+∠C=∠AEC+2∠DCE;
如图4,∵∠DEO=∠DEC,∠EDO=∠EDC,
∴∠DOE=∠DCE,
∵∠AEC是△OEH的外角,
∴∠AEC=∠DOE+∠OHE,
∵∠OHE是△CDH的外角,
∴∠OHE=∠CDB+∠C,
∴∠AEC=∠DOE+∠CDB+∠C=∠CDB+2∠DCE.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
