上海(沪教版)八年级下数学辅导讲义-第14讲-三角形、梯形的中位线教师版
文档属性
| 名称 | 上海(沪教版)八年级下数学辅导讲义-第14讲-三角形、梯形的中位线教师版 |

|
|
| 格式 | zip | ||
| 文件大小 | 291.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-28 00:00:00 | ||
图片预览



文档简介
学员姓名: 学科教师: 年 级: 辅导科目:
授课日期 ××年××月××日 时 间 A / B / C / D / E / F段
主 题 三角形、梯形的中位线
教学内容
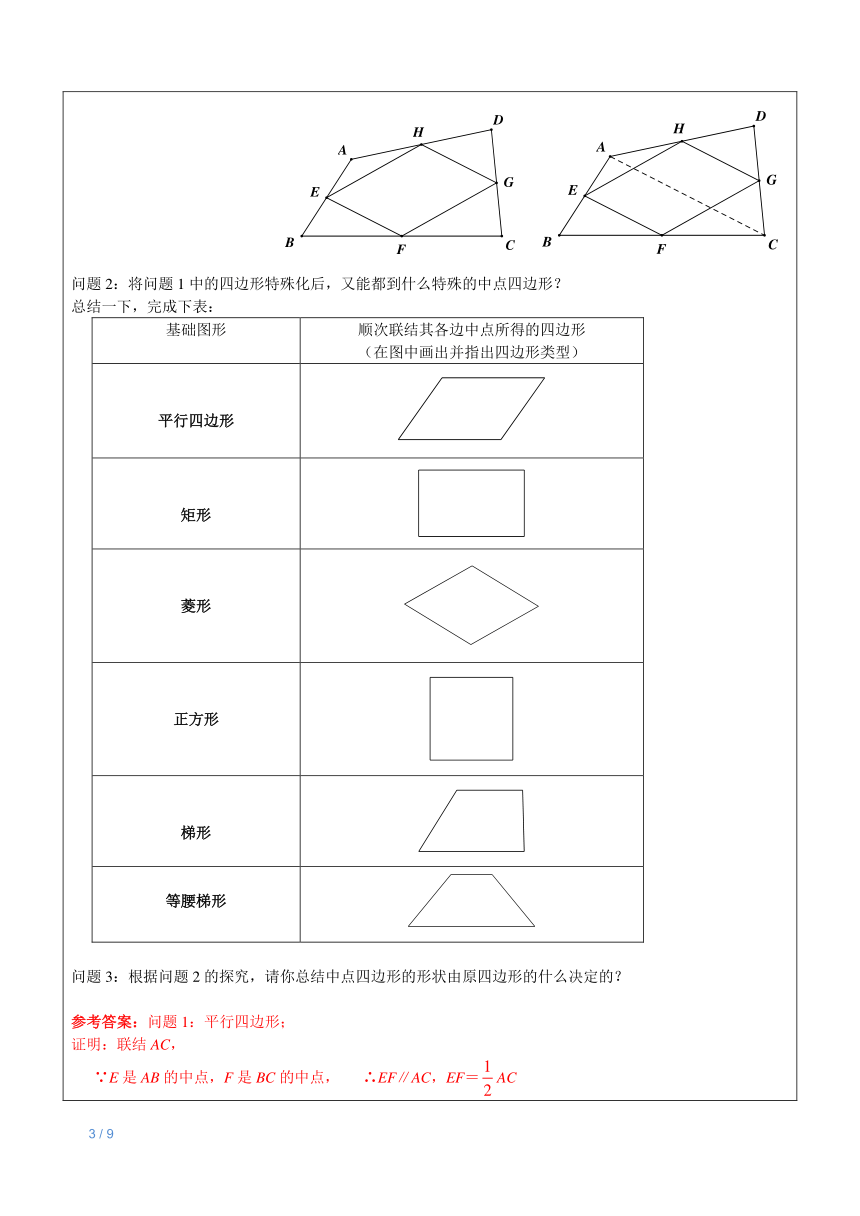
1.理解三角形、梯形的中位线概念; 2.掌握三角形、梯形中位线的性质定理,并能用其进行计算和论证; 3. 能综合运用三角形、梯形、以及其他特殊四边行有关知识进行计算与证明. (此环节设计时间在10-15分钟) 教法说明:首先回顾上次课的预习思考内容,建议让学生回顾证明三角形、梯形中位线的方法. 1.三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半; 2.梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半. 练习: 1.已知梯形的中位线长为9cm,上底长5cm,那么下底的长是 cm; 2.梯形的中位线长为20cm,高为4cm,则其面积为 cm?; 3.若梯形的中位线被它的两条对角线三等分,则梯形的上底a与下底b(a 问题3:根据问题2的探究,请你总结中点四边形的形状由原四边形的什么决定的? 参考答案:问题1:平行四边形; 证明:联结AC, ∵E是AB的中点,F是BC的中点, ∴EF∥AC,EF=AC 同理:HG∥AC,HG=AC ∴EF∥HG,EF=HG, ∴四边形EFGH是平行四边形. 问题2:略; 问题3:中点四边形的形状是由原四边形对角线的数量和位置关系决定的,当原四边形对角线相等时为菱形,对角线垂直时为矩形,对角线相等且垂直时为正方形. 例题3:如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC内,CE⊥AE,点F在边AB上,EF∥BC. (1)求证:四边形BDEF是平行四边形; (2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论. 参考答案:(1)证明:延长CE交AB于点G, ∵AE⊥CE,∴∠AEG=∠AEC=90?, 又∵∠GAE=∠CAE,AE=AE,∴△AGE≌△ACE. ∴GE=EC. ∵BD=CD,∴DE//AB. ∵EF//BC,∴四边形BDEF是平行四边形. (2)解:∵四边形BDEF是平行四边形,∴BF=DE. ∵D、E分别是BC、GC的中点,∴BG =2BF=2DE. ∵△AGE≌△ACE,∴AG=AC, ∴2BF=AB–AG=AB–AC. 例题4:如图,在梯形ABCD中,AB//CD,AD=BC,对角线AC、BD的交点O,∠AOB=60°,又S、P、Q分别是DO、AO、BC的中点. 求证:△SPQ是等边三角形. 参考答案: 证明:联结CS,BP. ∵四边形ABCD是等腰梯形,且AC与BD相交于O, ∴可得出:△CAB≌△DBA, ∴∠CAB=∠DBA, 同理可得出:∠ACD=∠BDC, ∴AO=BO,CO=DO. ∵∠AOB =60°, ∴△OCD与△OAB均为等边三角形. ∵S是OD的中点, ∴CS⊥DO. 在Rt△BSC中,Q为BC中点,SQ是斜边BC的中线, ∴SQ=BC. 同理BP⊥AC. 在Rt△BPC中,PQ=BC. 又∵SP是△OAD的中位线, ∴SP=AD=BC. ∴SP=PQ=SQ. 故△SPQ为等边三角形 ※例题5:如图在△ABC中,D、E分别为AB、AC上的点,且BD=CE,M、N分别是BE、CD的中点.过 MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么? 答案:AP=AQ, 理由:取BC的中点H,联结MH,NH. ∵M,H为BE,BC的中点, ∴MH∥EC,且MH=EC.
同理:NH∥BD,且NH=BD.
∵BD=CE,∴MH=NH.∴∠HMN=∠HNM;
∵MH∥EC,∴∠HMN=∠PQA,
同理∠HNM=∠QPA.
∴∠APQ=∠AQP, ∴AP=AQ 此环节设计时间在30分钟左右(20分钟练习+10分钟互动讲解)。 1.若顺次联结四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是 的四边形; 2.如图,在梯形ABCD中,已知AD//CB,对角线AC⊥BD,且AC=5cm,BD=12cm,则梯形的中位线长 为 cm; 3.已知:如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,求ED. 4.如图,AD平分∠BAC,交BC于点D,过C作AD的垂线,交AD的延长线于点E,F为BC中点,联结EF; 求证:EF//AB . 参考答案:1.对角线垂直; 2.; 3. ED=1,提示:延长BE,交AC于F点; 4.提示:延长AB和CE交于G点即可. 补充类试题: 已知:如图,在四边形ABCD中,AD=BC,E、F分别是DC、AB边的中点,FE的延长线分别与AD、BC 的延长线交于H、G点. 求证:∠AHF=∠BGF. 参考答案:联结AC,取AC的中点M,再分别联结ME、MF, ∵E、F分别是DC、AB边的中点,∴ME∥AD, EM=AD, MF∥BC,MF=BC. ∵AD=BC, ∴EM=MF, ∴∠MEF=∠MFE. ∵EM∥AH,∴∠MEF=∠AHF ∵FM∥BG,∴∠MFE=∠BGF ∴∠AHF=∠BGF (此环节设计时间在5-10分钟内) 让学生回顾本节课所学的重点知识,以学生自我总结为主,学科教师引导为辅,为本次课做一个总结回顾 【巩固练习】 1.如图,梯形ABCD中,E、F分别为腰AB 、CD的中点,若 ∠ABC和∠DCB的平分线相交与线段EF上的一点P,当EF=3时,则梯形ABCD的周长为 ; 2.等腰梯形的对角线互相垂直,若连接该等腰梯形各边中点,则所得图形是( ) A、平行四边形 B、矩形 C、菱形 D、正方形 3.如图,在梯形ABCD中,AD//BC,E、F、M分别为AB、DC、BC的中点,且ME = MF. 求证:梯形ABCD是等腰梯形. 4.如图,已知BE、CD分别是△ABC的角平分线,并且AE⊥BE于E点,AD⊥DC于D点.
求证:(1)DE∥BC;(2)DE=(AB+AC?BC). 参考答案:1.12; 2.D; 3.联结AC,BD, ∵E、F、M分别为AB、DC、BC的中点, ∴EM=AC,MF=BD, ∵ME = MF, ∴AC=BD, ∴梯形ABCD是等腰梯形 4.证明:(1)延长AD、AE,交BC于F、G; ∵BE⊥AG, ∴∠AEB=∠BEG=90°; ∵BE平分∠ABG,∴∠ABE=∠GBE; ∴∠BAE=∠BGE; ∴△ABG是等腰三角形; ∴AB=BG,即E是AG中点; 同理可得:D是AF中点; ∴DE是△AFG的中位线; ∴DE∥BC. (2)由(1)知DE是△AFG的中位线,∴DE=FG; ∵FG=BG+CF-BC,且AB=BG,AC=CF; ∴FG=AB+AC-BC,即DE=(AB+AC-BC) 【预习思考】 1.菱形的两条对角线之比是2:3,面积是27,则两条对角线的长分别是 和 . 2.如图,已知梯形ABCD的中位线为EF,且△AEF的面积为6cm2,则梯形ABCD的面积为( ) A、 12 cm2 B、 18 cm2 C、 24 cm2 D、30 cm2 3.已知四边形ABCD是平行四边形,下列结论中不正确的是( ) A、当AB=BC时,它是菱形; B、当AC⊥BD时,它是菱形; C、当AC=BD时,它是正方形; D、当∠ABC=900时,它是矩形. 4.下列说法:①一组对边平行,另一组对边相等的四边形是平行四边形或等腰梯形。 ②一组对边平行,一组对角相等的四边形是平行四边形。 ③两组对角分别相等的四边形是平行四边形。 ④顺次联结等腰梯形各边中点所得到的四边形是菱形。其中正确的是( ) A、①② B、①②③ C、②③④ D、①②③④
1
7 / 9
授课日期 ××年××月××日 时 间 A / B / C / D / E / F段
主 题 三角形、梯形的中位线
教学内容
1.理解三角形、梯形的中位线概念; 2.掌握三角形、梯形中位线的性质定理,并能用其进行计算和论证; 3. 能综合运用三角形、梯形、以及其他特殊四边行有关知识进行计算与证明. (此环节设计时间在10-15分钟) 教法说明:首先回顾上次课的预习思考内容,建议让学生回顾证明三角形、梯形中位线的方法. 1.三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半; 2.梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半. 练习: 1.已知梯形的中位线长为9cm,上底长5cm,那么下底的长是 cm; 2.梯形的中位线长为20cm,高为4cm,则其面积为 cm?; 3.若梯形的中位线被它的两条对角线三等分,则梯形的上底a与下底b(a
同理:NH∥BD,且NH=BD.
∵BD=CE,∴MH=NH.∴∠HMN=∠HNM;
∵MH∥EC,∴∠HMN=∠PQA,
同理∠HNM=∠QPA.
∴∠APQ=∠AQP, ∴AP=AQ 此环节设计时间在30分钟左右(20分钟练习+10分钟互动讲解)。 1.若顺次联结四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是 的四边形; 2.如图,在梯形ABCD中,已知AD//CB,对角线AC⊥BD,且AC=5cm,BD=12cm,则梯形的中位线长 为 cm; 3.已知:如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,求ED. 4.如图,AD平分∠BAC,交BC于点D,过C作AD的垂线,交AD的延长线于点E,F为BC中点,联结EF; 求证:EF//AB . 参考答案:1.对角线垂直; 2.; 3. ED=1,提示:延长BE,交AC于F点; 4.提示:延长AB和CE交于G点即可. 补充类试题: 已知:如图,在四边形ABCD中,AD=BC,E、F分别是DC、AB边的中点,FE的延长线分别与AD、BC 的延长线交于H、G点. 求证:∠AHF=∠BGF. 参考答案:联结AC,取AC的中点M,再分别联结ME、MF, ∵E、F分别是DC、AB边的中点,∴ME∥AD, EM=AD, MF∥BC,MF=BC. ∵AD=BC, ∴EM=MF, ∴∠MEF=∠MFE. ∵EM∥AH,∴∠MEF=∠AHF ∵FM∥BG,∴∠MFE=∠BGF ∴∠AHF=∠BGF (此环节设计时间在5-10分钟内) 让学生回顾本节课所学的重点知识,以学生自我总结为主,学科教师引导为辅,为本次课做一个总结回顾 【巩固练习】 1.如图,梯形ABCD中,E、F分别为腰AB 、CD的中点,若 ∠ABC和∠DCB的平分线相交与线段EF上的一点P,当EF=3时,则梯形ABCD的周长为 ; 2.等腰梯形的对角线互相垂直,若连接该等腰梯形各边中点,则所得图形是( ) A、平行四边形 B、矩形 C、菱形 D、正方形 3.如图,在梯形ABCD中,AD//BC,E、F、M分别为AB、DC、BC的中点,且ME = MF. 求证:梯形ABCD是等腰梯形. 4.如图,已知BE、CD分别是△ABC的角平分线,并且AE⊥BE于E点,AD⊥DC于D点.
求证:(1)DE∥BC;(2)DE=(AB+AC?BC). 参考答案:1.12; 2.D; 3.联结AC,BD, ∵E、F、M分别为AB、DC、BC的中点, ∴EM=AC,MF=BD, ∵ME = MF, ∴AC=BD, ∴梯形ABCD是等腰梯形 4.证明:(1)延长AD、AE,交BC于F、G; ∵BE⊥AG, ∴∠AEB=∠BEG=90°; ∵BE平分∠ABG,∴∠ABE=∠GBE; ∴∠BAE=∠BGE; ∴△ABG是等腰三角形; ∴AB=BG,即E是AG中点; 同理可得:D是AF中点; ∴DE是△AFG的中位线; ∴DE∥BC. (2)由(1)知DE是△AFG的中位线,∴DE=FG; ∵FG=BG+CF-BC,且AB=BG,AC=CF; ∴FG=AB+AC-BC,即DE=(AB+AC-BC) 【预习思考】 1.菱形的两条对角线之比是2:3,面积是27,则两条对角线的长分别是 和 . 2.如图,已知梯形ABCD的中位线为EF,且△AEF的面积为6cm2,则梯形ABCD的面积为( ) A、 12 cm2 B、 18 cm2 C、 24 cm2 D、30 cm2 3.已知四边形ABCD是平行四边形,下列结论中不正确的是( ) A、当AB=BC时,它是菱形; B、当AC⊥BD时,它是菱形; C、当AC=BD时,它是正方形; D、当∠ABC=900时,它是矩形. 4.下列说法:①一组对边平行,另一组对边相等的四边形是平行四边形或等腰梯形。 ②一组对边平行,一组对角相等的四边形是平行四边形。 ③两组对角分别相等的四边形是平行四边形。 ④顺次联结等腰梯形各边中点所得到的四边形是菱形。其中正确的是( ) A、①② B、①②③ C、②③④ D、①②③④
1
7 / 9
