上海(沪教版)八年级下数学辅导讲义-第18讲-概率初步教师版
文档属性
| 名称 | 上海(沪教版)八年级下数学辅导讲义-第18讲-概率初步教师版 |
|
|
| 格式 | zip | ||
| 文件大小 | 321.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-28 00:00:00 | ||
图片预览





文档简介
学员姓名: 学科教师: 年 级: 辅导科目:
授课日期 ××年××月××日 时 间 A / B / C / D / E / F段
主 题 概率初步
教学内容
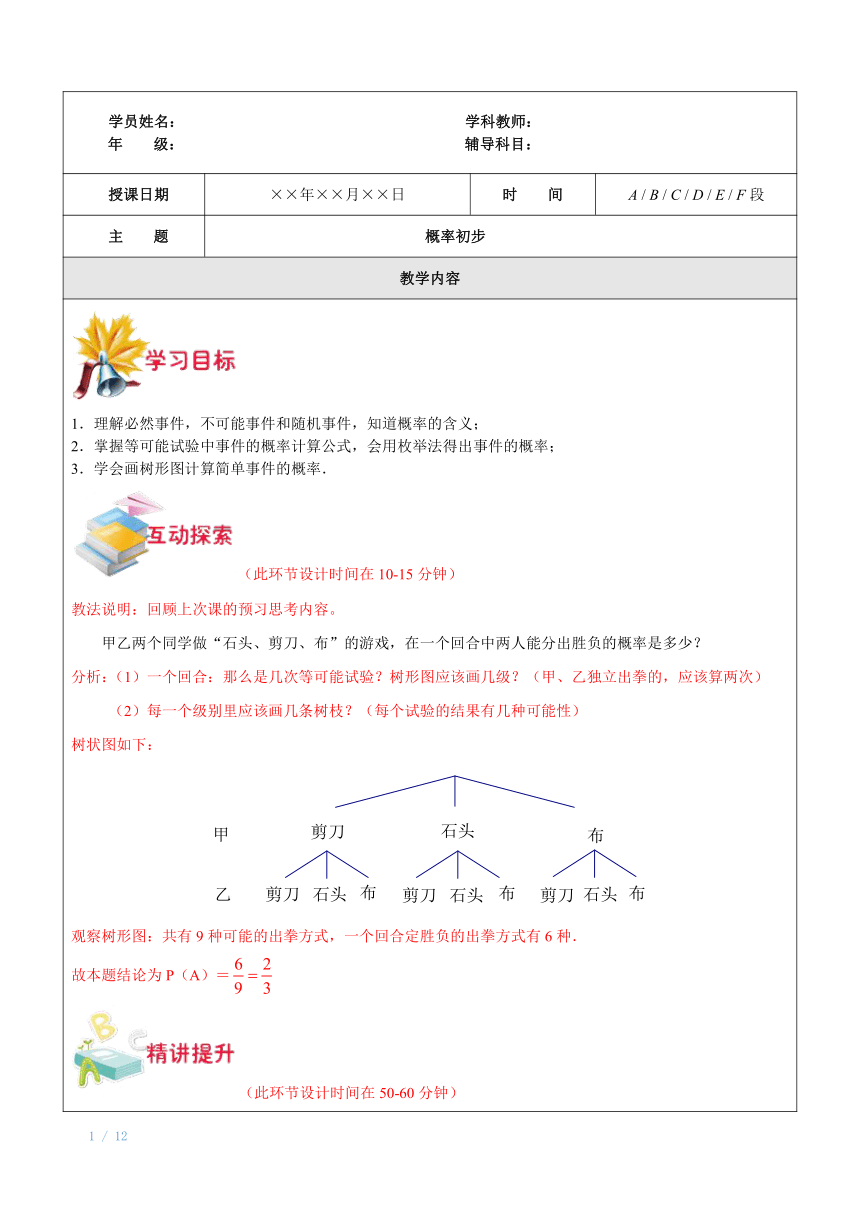
1.理解必然事件,不可能事件和随机事件,知道概率的含义; 2.掌握等可能试验中事件的概率计算公式,会用枚举法得出事件的概率; 3.学会画树形图计算简单事件的概率. (此环节设计时间在10-15分钟) 教法说明:回顾上次课的预习思考内容。 甲乙两个同学做“石头、剪刀、布”的游戏,在一个回合中两人能分出胜负的概率是多少? 分析:(1)一个回合:那么是几次等可能试验?树形图应该画几级?(甲、乙独立出拳的,应该算两次) (2)每一个级别里应该画几条树枝?(每个试验的结果有几种可能性) 树状图如下: 观察树形图:共有9种可能的出拳方式,一个回合定胜负的出拳方式有6种. 故本题结论为P(A)= (此环节设计时间在50-60分钟) 知识点1:随机事件、必然事件、不可能事件 在一定条件下必定出现的现象叫做必然事件;如果用U表示,则概率为1: P(U)=1; 在一定条件下必定不出现的现象叫做不可能事件;如果用V表示,则概率为0: P(V)=0; 在一定条件下可能出现也可能不出现的现象叫做随机事件(不确定事件);一般用A表示,则概率P(A)介于0到1之间;P(A)——纯小数、真分数、百分数等表示. 例题1:下列语句正确的是( ) A、“上海冬天最低气温低于-5℃”,这是必然事件; B、“在去掉大小王的52张扑克牌中抽13张牌,其中有4张黑桃”,这是必然事件; C、“电视打开时正在播放广告”,这是不可能事件; D、“从由1,2,5组成的没有重复数字的三位数中任意抽取一个数,这个三位数能被4整除”,这是随机事件. 参考答案:D 试一试: 1.下列成语或词语所反映的事件中,可能性大小最小的是( ) . A、瓮中捉鳖; B、守株待兔; C、旭日东升; D、夕阳西下. 2.在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中黄球1个,红球1个,白球2个,“从中任意摸出2个球,它们的颜色相同”这一事件是( ) A.必然事件; B.不可能事件; C.随机事件; D.确定事件. 参考答案:1.B; 2.C. 知识点2:事件发生的可能性 例题2:事件“钟面上时针与分针成一直线”发生的可能性( ) A、不可能; B、可能性很小; C、可能性很大; D、以上都不对. 参考答案:B 试一试: 1.投掷一枚普通的六面体骰子,有下列事件: ①掷得的点数是6;②掷得的点数是奇数;③掷得的点数不大于4;④掷得的点数不小于2;这些事件发生的可能性由大到小排列正确的是( ) A、①②③④; B、④③②①; C、③④②①; D、②③①④. 2.木盒里有10个红球,3个黄球和1个白球,这些球只是颜色不同,大小一样;从木盒中任意摸出1个球,①摸出1个黄球;②摸出1个白球;③摸出1个绿球;④摸出一个红球;⑤摸出一个球颜色是黄色或者白色;这些事情发生可能性的大小从大到小排列为 . 参考答案:1.B; 2.④⑤①②③. 知识点3:概率的理解 例题3:气象台预报“本市明天降水概率是80%”,对此信息,下面的几种说法正确的是( ) A、本市明天将有80%的地区降水; B、本市明天将有80%的时间降水; C、明天肯定下雨; D、明天降水的可能性比较大. 参考答案:D 试一试: 1.下列说法正确的是( ) A.“明天的降水概率为30%”是指明天下雨的可能性是30%; B.连续抛一枚硬币50次,出现正面朝上的次数一定是25次; C.连续三次掷一颗骰子都出现了奇数,则第四次出现的数一定是偶数; D.某地发行一种福利彩票,中奖概率为1%,买这种彩票100张一定会中奖. 2.下列事件中,概率接近于1的是( ) A、大晴天出门遇到下冰雹; B、在1到10的十个整数中任取一个数恰是偶数; C、自然数1是素数; D、买了一张福利彩票,但没有中奖. 参考答案:1.A; 2.D. 知识点4:频率与概率的关系 例题4:甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( ) A、掷一枚正六面体的骰子,出现1点的概率; B、抛一枚硬币,出现正面的概率; C、任意写一个整数,它能2被整除的概率; D、从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率. 参考答案:D 试一试: 1.在一个不透明的盒子里装着若干个白球,小明想估计其中的白球数,于是他放入10个黑球,搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,得到如下数据: 摸球的次数n20406080120160200摸到白球的次数m1533496397128158摸到白球的频率0.750.830.820.790.810.800.79
估算盒子里白球的个数为( ) A、8个; B、40个; C、80个; D、无法估计. 2.下列说法正确的有( ) A、在一次抛掷硬币的试验中,甲同学说:“我只做了10次试验就得到了正面朝上的概率为30%”; B、某同学在抛掷两枚硬币的试验中做了400次,得到“一正一反”的频率为26.7%,如果再做400次,得到的频率仍然是26.7%; C、在投掷一枚均匀的正方体骰子的试验中,小明得到“1点朝上”的概率为,那么他再做300次试验,一定有50次“1点朝上”; D、在抛掷一枚硬币的试验中,小刚为了节约时间,同时抛掷5枚硬币,这样得到的结果不会受到影响. 参考答案:1.B; 2.D. 知识点5:等可能事件概率的计算 例题5: (1)从1,2,3,4,5,6中任意取一个数,取到的数是6的因数的概率是( ) A、; B、; C、; D、. (2)在一个不透明的袋子中装有2个白球,n个红球,它们除了颜色不同外,其余均相同.若从中随机摸出一个球,摸到红球的概率是,则n的值等于 . (3)同时抛掷两枚质地均匀的正方形骰子,出现“朝上两面的点数和为奇数”的概率为 . 参考答案:(1)C; (2)8; (3); 试一试: 1.在0、1、2三个数中任取两个,组成两位数,则在组成的两位数中是奇数的概率为 . 2.用0,4,5三个数字组成的三位数中能被5整除的概率是 . 参考答案:1.; 2.; 知识点6:利用树状图法或列表法求概率 例题6:如图,转盘A等分为四个扇形,号码为1、2、3、4;转盘B等分为六个扇形,号码为1、2、3、4、5、6,甲乙两位同学想这样玩游戏:甲任意转动A盘,停止时指针得到一个号码;乙任意转动B盘,停止时指针得到一个号码(当指针落在扇形边界时,统计在逆时针方向相邻的扇形内)如果两号码的积为奇数,那么甲胜;如果两号码的积为偶数,那么乙胜;判断这个游戏是否公平,如果不公平,请设计一个公平的游戏规则. 参考答案:不公平(画树状图);设计略. 试一试:在一个口袋中,装有除颜色外其他完全相同的2个红球和2个白球,从中随机摸出两个球,摸到两个球颜色不同的概率是 . 参考答案: 知识点7:转化为面积问题的概率计算 例题7:如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,矩形ABCD内的一个动点P落在阴影部分的概率是 ; 参考答案: 试一试: 1.一矩形场地内有两相邻的正方形,面积分别为2和8,(如图)小明随机地向场地进行丢石子实验,则石子落在阴影部分的概率是 ; 2.如图两块完全相同的正方形木板重叠而成的,其中一个正方形的一个顶点恰好落在另一个正方形的中心O,现有一个机器猫在上面走动,则机器猫恰好落在重叠区域的概率是 ; 参考答案:1.; 2. 此环节设计时间在30分钟左右(20分钟练习+10分钟互动讲解)。 1.如图,飞镖投一个被平均分成6份的圆形靶子,那么飞镖落在阴影部分的概率是( ). A、; B、; C、; D、. 2.有8只型号相同的杯子,其中一等品5只,二等品2只和三等品1只,从中随机抽取 1只杯子,恰好是一等品的概率是 . 3.布袋中装有3个红球和6个白球,它们除颜色外其他都相同,如果从布袋里随机摸出一个球,那么所摸到的球恰好为红球的概率是 . 4.将“定理”的英文单词theorem中的7个字母分别写在7张相同的卡片上,字面朝下随意放在桌子上,任取一张,那么取到字母e的概率为?_________?. 5.口袋里装有个白球和个黑球,从中任意取出个球,设事件A“取到的个球都是白球”和事件B“取到的个球都是黑球”的概率分别为P(A)、P(B),则( ) A、P(A)=P(B); B、P(A)>P(B);C、P(A)①打开电视,正在播广告;
②投掷一枚普通的骰子,掷得的点数小于10;
③射击运动员射击一次,命中10环;
④在一个只装有红球的袋中摸出白球. A、0; B、1; C、2; D、3 2.甲、乙两人各自投掷一个普通的正方体骰子,如果两者之积为奇数,那么甲得1分;如果两者之积为偶数,那么乙得1分,连续投掷20次,谁得分高,谁就获胜.请你用掌握的数学知识分析,谁获胜的可能性大?( ) A、甲; B、乙; C、甲、乙一样; D、不能确定 3.如图,一飞镖游戏板,其中每个小正方形的大小相等,则随意投掷一个飞镖,击中黑色区域的概率是( ) A、; B、; C、; D、 4.布袋中有两个红球和两个白球,它们除颜色外其它都相同,从布袋中一次摸出两个球,事件“一次摸出的两个球都是白球”的概率是__ ____. 5.在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上. (1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是 ; (2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图或列表法求解). 参考答案:1.C; 2.B; 3.B; 4.; 5.(1); (2); 【预习思考】 期末小测试 (测试时间30分钟,满分50分) 一、选择题(本大题共3题,每题4分,满分12分) 1.对于二项方程,当为偶数时,已知方程有两个实数根,那么下列不等式成立的是( ) (A); (B); (C); (D). 2.已知一次函数,则下列判断错误的是 ( ) (A)直线在轴上的截距为; (B)直线不经过第二象限; (C)直线在轴上方的点的横坐标的取值范围是; (D)该一次函数的函数值随自变量的值增大而增大. 3.已知四边形中,,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( ) (A); (B); (C); (D). 二、填空题(本大题共3题,每题4分,满分12分) 4.已知:正方形ABCD的边长等于8cm,那么边AB的中点M到对角线BD的距离等于 cm. 5.在梯形中,∥,,cm,cm,cm,则的长 为 cm. 6.如图,已知菱形ABCD的边长为2,∠A=45°,将菱形ABCD绕点A旋转45°,得到菱形,其中B、C、D的对应点分别是,那么点的距离为 . 7.(本题12分)如图,在□ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作AG//DB交CB的延长线于点G. (1)求证:DE∥BF; (2)若∠G=,求证:四边形DEBF是菱形. 8.(本题14分)已知: O为正方形ABCD对角线的交点,点E在边CB的延长线上,联结EO,OF⊥OE交BA延长线于点F,联结EF(如图)。 求证:EO=FO; 若正方形的边长为2, OE=2OA,求BE的长; 答案及评分标准 选择题 A; 2、C; 3、C。 二、填空题 4、; 5、2或8; 6、 三、解答题 7、证明:(1)∵□ABCD ,∴AB∥CD,AB=CD-----------------------------------2分 ∵E、F分别为AB、CD的中点,∴DF=DC,BE=AB ∴DF∥BE,DF=BE---------------------------------------------------------------------2分 ∴四边形DEBF为平行四边形 ∴DE∥BF-----------------------------------------------------------------------------------2分 (2)证明:∵AG∥BD,∴∠G=∠DBC=90°,∴DBC 为直角三角形---2分 又∵F为边CD的中点.∴BF=DC=DF------------------------------------------2分 又∵四边形DEBF为平行四边形,∴四边形DEBF是菱形----------------------2分 8、(1)证明:∵ABCD是正方形,对角线交于点O, ∴AO=BO,AC⊥BD,-----------------------------------------------------------2分 ∴ ∠OAB=∠OBA,∴∠OAF=∠OBE,--------------------------------------2分 ∵AC⊥BD,OF⊥OE,∴∠AOF==∠BOE,------------2分 ∴△AOF≌△BOE, ∴EO=FO.----------------------------------------------------------------------------1分 (2)解:∵ABCD是正方形,边长为2,∴AO=,∴OE=2OA= ∵OF⊥OE,EO=FO,∴EF=4,--------------------------------------------------2分 ∵△AOF≌△BOE,∴AF=BE,--------------------------------------------------2分 设AF=BE=x, 在Rt△EFB中,,即 解得,∵x>0,∴,即BE=---------------3分
1
11 / 12
授课日期 ××年××月××日 时 间 A / B / C / D / E / F段
主 题 概率初步
教学内容
1.理解必然事件,不可能事件和随机事件,知道概率的含义; 2.掌握等可能试验中事件的概率计算公式,会用枚举法得出事件的概率; 3.学会画树形图计算简单事件的概率. (此环节设计时间在10-15分钟) 教法说明:回顾上次课的预习思考内容。 甲乙两个同学做“石头、剪刀、布”的游戏,在一个回合中两人能分出胜负的概率是多少? 分析:(1)一个回合:那么是几次等可能试验?树形图应该画几级?(甲、乙独立出拳的,应该算两次) (2)每一个级别里应该画几条树枝?(每个试验的结果有几种可能性) 树状图如下: 观察树形图:共有9种可能的出拳方式,一个回合定胜负的出拳方式有6种. 故本题结论为P(A)= (此环节设计时间在50-60分钟) 知识点1:随机事件、必然事件、不可能事件 在一定条件下必定出现的现象叫做必然事件;如果用U表示,则概率为1: P(U)=1; 在一定条件下必定不出现的现象叫做不可能事件;如果用V表示,则概率为0: P(V)=0; 在一定条件下可能出现也可能不出现的现象叫做随机事件(不确定事件);一般用A表示,则概率P(A)介于0到1之间;P(A)——纯小数、真分数、百分数等表示. 例题1:下列语句正确的是( ) A、“上海冬天最低气温低于-5℃”,这是必然事件; B、“在去掉大小王的52张扑克牌中抽13张牌,其中有4张黑桃”,这是必然事件; C、“电视打开时正在播放广告”,这是不可能事件; D、“从由1,2,5组成的没有重复数字的三位数中任意抽取一个数,这个三位数能被4整除”,这是随机事件. 参考答案:D 试一试: 1.下列成语或词语所反映的事件中,可能性大小最小的是( ) . A、瓮中捉鳖; B、守株待兔; C、旭日东升; D、夕阳西下. 2.在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中黄球1个,红球1个,白球2个,“从中任意摸出2个球,它们的颜色相同”这一事件是( ) A.必然事件; B.不可能事件; C.随机事件; D.确定事件. 参考答案:1.B; 2.C. 知识点2:事件发生的可能性 例题2:事件“钟面上时针与分针成一直线”发生的可能性( ) A、不可能; B、可能性很小; C、可能性很大; D、以上都不对. 参考答案:B 试一试: 1.投掷一枚普通的六面体骰子,有下列事件: ①掷得的点数是6;②掷得的点数是奇数;③掷得的点数不大于4;④掷得的点数不小于2;这些事件发生的可能性由大到小排列正确的是( ) A、①②③④; B、④③②①; C、③④②①; D、②③①④. 2.木盒里有10个红球,3个黄球和1个白球,这些球只是颜色不同,大小一样;从木盒中任意摸出1个球,①摸出1个黄球;②摸出1个白球;③摸出1个绿球;④摸出一个红球;⑤摸出一个球颜色是黄色或者白色;这些事情发生可能性的大小从大到小排列为 . 参考答案:1.B; 2.④⑤①②③. 知识点3:概率的理解 例题3:气象台预报“本市明天降水概率是80%”,对此信息,下面的几种说法正确的是( ) A、本市明天将有80%的地区降水; B、本市明天将有80%的时间降水; C、明天肯定下雨; D、明天降水的可能性比较大. 参考答案:D 试一试: 1.下列说法正确的是( ) A.“明天的降水概率为30%”是指明天下雨的可能性是30%; B.连续抛一枚硬币50次,出现正面朝上的次数一定是25次; C.连续三次掷一颗骰子都出现了奇数,则第四次出现的数一定是偶数; D.某地发行一种福利彩票,中奖概率为1%,买这种彩票100张一定会中奖. 2.下列事件中,概率接近于1的是( ) A、大晴天出门遇到下冰雹; B、在1到10的十个整数中任取一个数恰是偶数; C、自然数1是素数; D、买了一张福利彩票,但没有中奖. 参考答案:1.A; 2.D. 知识点4:频率与概率的关系 例题4:甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图所示,则符合这一结果的实验可能是( ) A、掷一枚正六面体的骰子,出现1点的概率; B、抛一枚硬币,出现正面的概率; C、任意写一个整数,它能2被整除的概率; D、从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率. 参考答案:D 试一试: 1.在一个不透明的盒子里装着若干个白球,小明想估计其中的白球数,于是他放入10个黑球,搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,得到如下数据: 摸球的次数n20406080120160200摸到白球的次数m1533496397128158摸到白球的频率0.750.830.820.790.810.800.79
估算盒子里白球的个数为( ) A、8个; B、40个; C、80个; D、无法估计. 2.下列说法正确的有( ) A、在一次抛掷硬币的试验中,甲同学说:“我只做了10次试验就得到了正面朝上的概率为30%”; B、某同学在抛掷两枚硬币的试验中做了400次,得到“一正一反”的频率为26.7%,如果再做400次,得到的频率仍然是26.7%; C、在投掷一枚均匀的正方体骰子的试验中,小明得到“1点朝上”的概率为,那么他再做300次试验,一定有50次“1点朝上”; D、在抛掷一枚硬币的试验中,小刚为了节约时间,同时抛掷5枚硬币,这样得到的结果不会受到影响. 参考答案:1.B; 2.D. 知识点5:等可能事件概率的计算 例题5: (1)从1,2,3,4,5,6中任意取一个数,取到的数是6的因数的概率是( ) A、; B、; C、; D、. (2)在一个不透明的袋子中装有2个白球,n个红球,它们除了颜色不同外,其余均相同.若从中随机摸出一个球,摸到红球的概率是,则n的值等于 . (3)同时抛掷两枚质地均匀的正方形骰子,出现“朝上两面的点数和为奇数”的概率为 . 参考答案:(1)C; (2)8; (3); 试一试: 1.在0、1、2三个数中任取两个,组成两位数,则在组成的两位数中是奇数的概率为 . 2.用0,4,5三个数字组成的三位数中能被5整除的概率是 . 参考答案:1.; 2.; 知识点6:利用树状图法或列表法求概率 例题6:如图,转盘A等分为四个扇形,号码为1、2、3、4;转盘B等分为六个扇形,号码为1、2、3、4、5、6,甲乙两位同学想这样玩游戏:甲任意转动A盘,停止时指针得到一个号码;乙任意转动B盘,停止时指针得到一个号码(当指针落在扇形边界时,统计在逆时针方向相邻的扇形内)如果两号码的积为奇数,那么甲胜;如果两号码的积为偶数,那么乙胜;判断这个游戏是否公平,如果不公平,请设计一个公平的游戏规则. 参考答案:不公平(画树状图);设计略. 试一试:在一个口袋中,装有除颜色外其他完全相同的2个红球和2个白球,从中随机摸出两个球,摸到两个球颜色不同的概率是 . 参考答案: 知识点7:转化为面积问题的概率计算 例题7:如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,矩形ABCD内的一个动点P落在阴影部分的概率是 ; 参考答案: 试一试: 1.一矩形场地内有两相邻的正方形,面积分别为2和8,(如图)小明随机地向场地进行丢石子实验,则石子落在阴影部分的概率是 ; 2.如图两块完全相同的正方形木板重叠而成的,其中一个正方形的一个顶点恰好落在另一个正方形的中心O,现有一个机器猫在上面走动,则机器猫恰好落在重叠区域的概率是 ; 参考答案:1.; 2. 此环节设计时间在30分钟左右(20分钟练习+10分钟互动讲解)。 1.如图,飞镖投一个被平均分成6份的圆形靶子,那么飞镖落在阴影部分的概率是( ). A、; B、; C、; D、. 2.有8只型号相同的杯子,其中一等品5只,二等品2只和三等品1只,从中随机抽取 1只杯子,恰好是一等品的概率是 . 3.布袋中装有3个红球和6个白球,它们除颜色外其他都相同,如果从布袋里随机摸出一个球,那么所摸到的球恰好为红球的概率是 . 4.将“定理”的英文单词theorem中的7个字母分别写在7张相同的卡片上,字面朝下随意放在桌子上,任取一张,那么取到字母e的概率为?_________?. 5.口袋里装有个白球和个黑球,从中任意取出个球,设事件A“取到的个球都是白球”和事件B“取到的个球都是黑球”的概率分别为P(A)、P(B),则( ) A、P(A)=P(B); B、P(A)>P(B);C、P(A)
②投掷一枚普通的骰子,掷得的点数小于10;
③射击运动员射击一次,命中10环;
④在一个只装有红球的袋中摸出白球. A、0; B、1; C、2; D、3 2.甲、乙两人各自投掷一个普通的正方体骰子,如果两者之积为奇数,那么甲得1分;如果两者之积为偶数,那么乙得1分,连续投掷20次,谁得分高,谁就获胜.请你用掌握的数学知识分析,谁获胜的可能性大?( ) A、甲; B、乙; C、甲、乙一样; D、不能确定 3.如图,一飞镖游戏板,其中每个小正方形的大小相等,则随意投掷一个飞镖,击中黑色区域的概率是( ) A、; B、; C、; D、 4.布袋中有两个红球和两个白球,它们除颜色外其它都相同,从布袋中一次摸出两个球,事件“一次摸出的两个球都是白球”的概率是__ ____. 5.在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上. (1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是 ; (2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图或列表法求解). 参考答案:1.C; 2.B; 3.B; 4.; 5.(1); (2); 【预习思考】 期末小测试 (测试时间30分钟,满分50分) 一、选择题(本大题共3题,每题4分,满分12分) 1.对于二项方程,当为偶数时,已知方程有两个实数根,那么下列不等式成立的是( ) (A); (B); (C); (D). 2.已知一次函数,则下列判断错误的是 ( ) (A)直线在轴上的截距为; (B)直线不经过第二象限; (C)直线在轴上方的点的横坐标的取值范围是; (D)该一次函数的函数值随自变量的值增大而增大. 3.已知四边形中,,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( ) (A); (B); (C); (D). 二、填空题(本大题共3题,每题4分,满分12分) 4.已知:正方形ABCD的边长等于8cm,那么边AB的中点M到对角线BD的距离等于 cm. 5.在梯形中,∥,,cm,cm,cm,则的长 为 cm. 6.如图,已知菱形ABCD的边长为2,∠A=45°,将菱形ABCD绕点A旋转45°,得到菱形,其中B、C、D的对应点分别是,那么点的距离为 . 7.(本题12分)如图,在□ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作AG//DB交CB的延长线于点G. (1)求证:DE∥BF; (2)若∠G=,求证:四边形DEBF是菱形. 8.(本题14分)已知: O为正方形ABCD对角线的交点,点E在边CB的延长线上,联结EO,OF⊥OE交BA延长线于点F,联结EF(如图)。 求证:EO=FO; 若正方形的边长为2, OE=2OA,求BE的长; 答案及评分标准 选择题 A; 2、C; 3、C。 二、填空题 4、; 5、2或8; 6、 三、解答题 7、证明:(1)∵□ABCD ,∴AB∥CD,AB=CD-----------------------------------2分 ∵E、F分别为AB、CD的中点,∴DF=DC,BE=AB ∴DF∥BE,DF=BE---------------------------------------------------------------------2分 ∴四边形DEBF为平行四边形 ∴DE∥BF-----------------------------------------------------------------------------------2分 (2)证明:∵AG∥BD,∴∠G=∠DBC=90°,∴DBC 为直角三角形---2分 又∵F为边CD的中点.∴BF=DC=DF------------------------------------------2分 又∵四边形DEBF为平行四边形,∴四边形DEBF是菱形----------------------2分 8、(1)证明:∵ABCD是正方形,对角线交于点O, ∴AO=BO,AC⊥BD,-----------------------------------------------------------2分 ∴ ∠OAB=∠OBA,∴∠OAF=∠OBE,--------------------------------------2分 ∵AC⊥BD,OF⊥OE,∴∠AOF==∠BOE,------------2分 ∴△AOF≌△BOE, ∴EO=FO.----------------------------------------------------------------------------1分 (2)解:∵ABCD是正方形,边长为2,∴AO=,∴OE=2OA= ∵OF⊥OE,EO=FO,∴EF=4,--------------------------------------------------2分 ∵△AOF≌△BOE,∴AF=BE,--------------------------------------------------2分 设AF=BE=x, 在Rt△EFB中,,即 解得,∵x>0,∴,即BE=---------------3分
1
11 / 12
