人教版数学八年级下册18.1.2平行四边形的判定课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.1.2平行四边形的判定课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-28 10:56:34 | ||
图片预览




文档简介
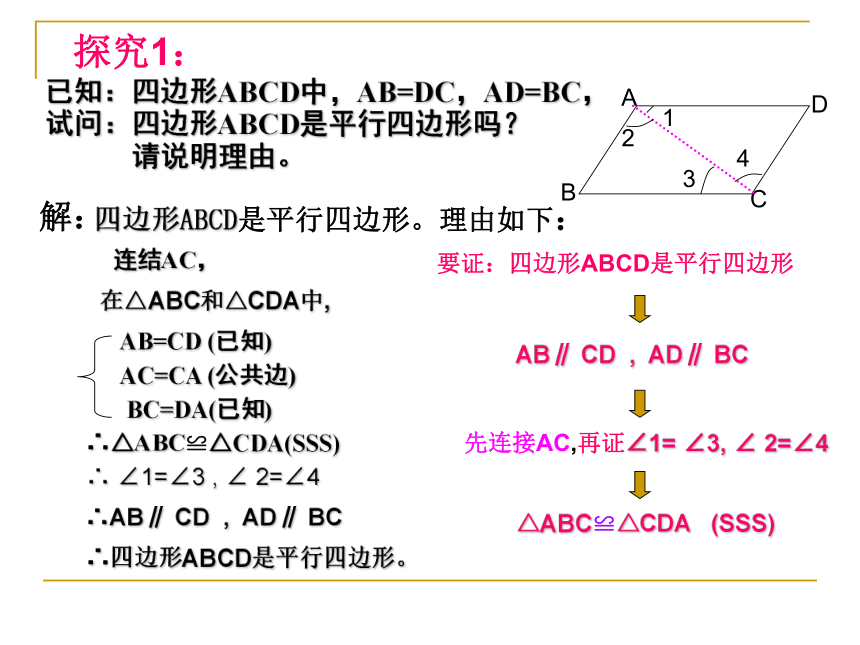
课件21张PPT。18.1.2平行四边形的判定 通过前面的学习,我们知道,平行四边形对边相等、对角相等、对角线互相平分。那么反过来,对边相等或对角相等或对角线互相平分的四边形是不是平行四边形呢?创设情境,引入新课有两组对边分别平行的四边形叫做平行四边形性质:平行四边形的对边相等平行四边形的对角相等平行四边形的对角线互相平分定义:探究1:已知:四边形ABCD中,AB=DC,AD=BC,试问:四边形ABCD是平行四边形吗?
请说明理由。要证:四边形ABCD是平行四边形AB∥ CD , AD∥ BC先连接AC,再证∠1= ∠3, ∠ 2=∠4
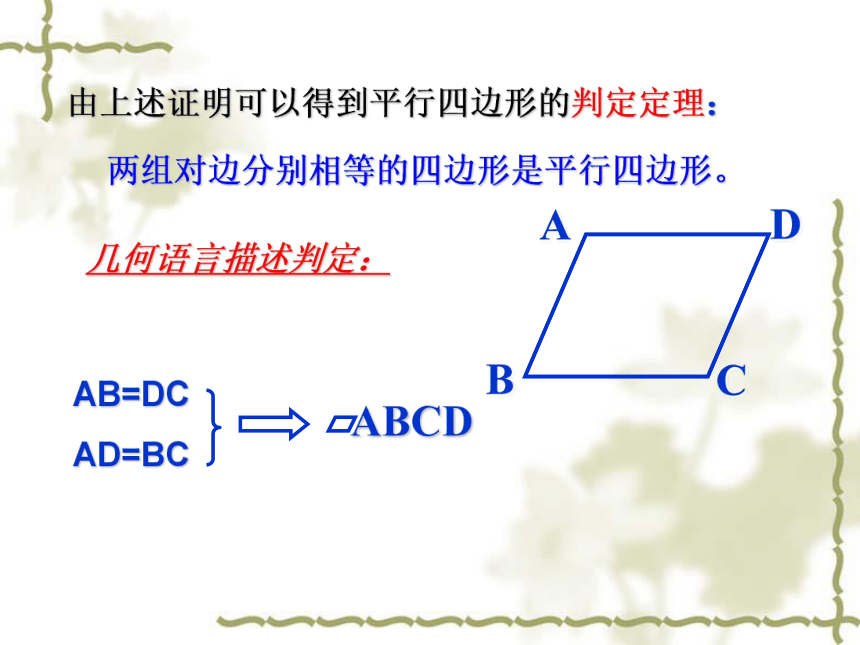
△ABC≌△CDA (SSS)解:四边形ABCD是平行四边形。理由如下:连结AC,AB=CD (已知)AC=CA (公共边)BC=DA(已知)∴△ABC≌△CDA(SSS)在△ABC和△CDA中,∴ ∠1=∠3 , ∠ 2=∠4∴AB∥ CD , AD∥ BC∴四边形ABCD是平行四边形。1234由上述证明可以得到平行四边形的判定定理:两组对边分别相等的四边形是平行四边形。几何语言描述判定:探究2已知:四边形ABCD中, ∠A=∠C ,∠B=∠D.
试问:四边 形ABCD是平行四边形吗?请说明理由。探究3已知:四边形ABCD中,OA=OC OB=OD,
试问:四边 形ABCD是平行四边形吗?请说明理由。探究2已知:四边形ABCD中, ∠A=∠C ,∠B=∠D.
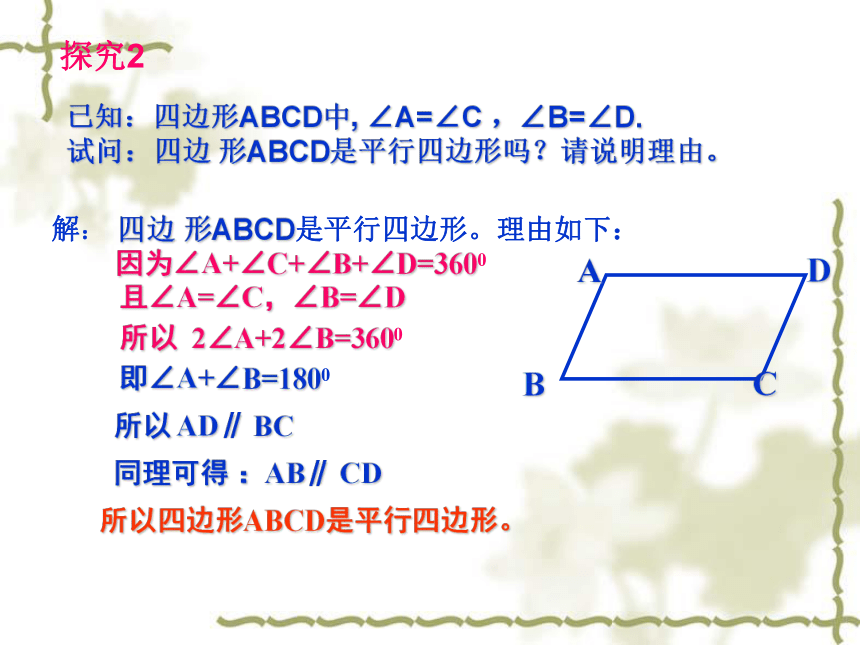
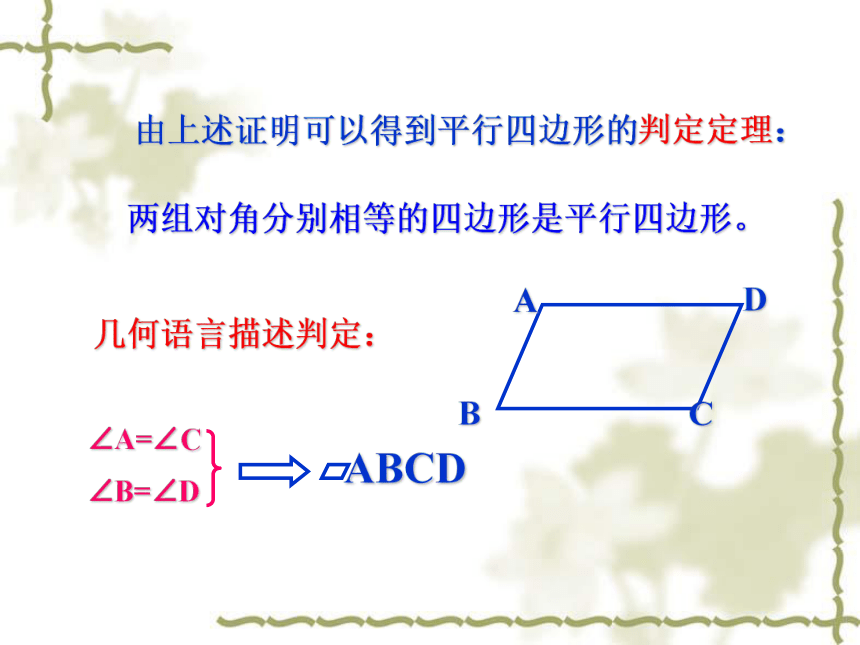
试问:四边 形ABCD是平行四边形吗?请说明理由。解:四边 形ABCD是平行四边形。理由如下:因为∠A+∠C+∠B+∠D=3600且∠A=∠C,∠B=∠D所以 2∠A+2∠B=3600即∠A+∠B=1800所以 AD∥ BC同理可得 :AB∥ CD所以四边形ABCD是平行四边形。由上述证明可以得到平行四边形的判定定理:两组对角分别相等的四边形是平行四边形。几何语言描述判定:∠A=∠C
∠B=∠D探究3已知:四边形ABCD中,OA=OC OB=OD,
试问:四边 形ABCD是平行四边形吗?
请说明理由。AB∥ CD , AD∥ BC△AOB≌△COD ,△AOD≌△COB要证:四边形ABCD是平行四边形∠ABO=∠CDO, ∠ DAO=∠BCO解:四边形ABCD是平行四边形。理由如下:在△ABO和△CDO中,AO=CO(已知)∠AOB=∠COD (对顶角相等)BO=DO(已知)所以△AOB≌△COD (SAS)所以 ∠ABO=∠CDO所以 AB∥ CD 所以四边形ABCD是平行四边形同理 AD∥ BC对角线互相平分的四边形是平行四边形。几何语言描述判定:AO=CO
BO=DO由上述证明可以得到平行四边形的判定定理:三、应用练习1、下面给出了四边形ABCD中 ∠A,∠B,∠C,∠D
的度数之比,其中能判定四边形ABCD是平行四边形的 是( )A.1:2:3:4 C.2:3:2:3 B.2:2:3:3 需要两组对角分别相等.D.2:3:3:2C 需要两组对边分别相等
或对角分别相等B 3、填空题:如图,
在四边形ABCD中,①如果AD=8cm,AB=4cm,且BC=___cm, CD=____cm,那么四边形ABCD是平行四边形。②若∠A=1200,则∠B=____0,∠C=____0,∠D=____0时,四边形ABCD是平行四边形。③如果AC=10cm,BD=12cm,且OA=___cm,0B=___cm,那么四边形ABCD是平行四边形。84点评:两组对边分别相等的四边形是平行四边形6012060点评:两组对角分别相等的四边形是平行四边形5点评:对角线互相平分的四边形是平行四边形6大显身手证明:因为四边形ABCD是平行四边形所以 AD ∥ BC且AD =BC所以 DE=BF所以四边形BFDE是平行四边形同理:BE=DF例、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形(两组对边分别相等的四边形是平行四边形)
例、已知:E、F是平行四边形ABCD对角线AC上的两点,
并且AE=CF。
求证:四边形BFDE是平行四边形.O证明:连接BD,交AC于点O.因为四边形ABCD是平行四边形 因为AE=CF
所以AO-AE=CO-CF即 EO=FO
又因为BO=DO
所以四边形BFDE是平行四边形.(对角线互相平分的四边形是平行四边形)
大显身手所以AO=CO,BO=DO1、已知:E、F是平行四边形ABCD对角线AC上的两点,当点E,F满足什么条件时,四边形BFDE是平行四边形?DOABCEF变式练习2、若E、F 移至OA、OC 的延长线上,且AE=CF,结论有改变吗?为什么?
变式练习 判定 1 定义:两组对边分别平行的四边形是平行四边形。 判定2 两组对边分别相等的四边形是平行四边形。 判定3 两组对角分别相等的四边形是平行四边形。 判定4 两条对角线互相平分的四边形是平行四边形。本节 课主要学习了平行四边形的判定定理:平行四边形的判别方法课本P50第5,P67第2题。作业布置新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!再 见
请说明理由。要证:四边形ABCD是平行四边形AB∥ CD , AD∥ BC先连接AC,再证∠1= ∠3, ∠ 2=∠4
△ABC≌△CDA (SSS)解:四边形ABCD是平行四边形。理由如下:连结AC,AB=CD (已知)AC=CA (公共边)BC=DA(已知)∴△ABC≌△CDA(SSS)在△ABC和△CDA中,∴ ∠1=∠3 , ∠ 2=∠4∴AB∥ CD , AD∥ BC∴四边形ABCD是平行四边形。1234由上述证明可以得到平行四边形的判定定理:两组对边分别相等的四边形是平行四边形。几何语言描述判定:探究2已知:四边形ABCD中, ∠A=∠C ,∠B=∠D.
试问:四边 形ABCD是平行四边形吗?请说明理由。探究3已知:四边形ABCD中,OA=OC OB=OD,
试问:四边 形ABCD是平行四边形吗?请说明理由。探究2已知:四边形ABCD中, ∠A=∠C ,∠B=∠D.
试问:四边 形ABCD是平行四边形吗?请说明理由。解:四边 形ABCD是平行四边形。理由如下:因为∠A+∠C+∠B+∠D=3600且∠A=∠C,∠B=∠D所以 2∠A+2∠B=3600即∠A+∠B=1800所以 AD∥ BC同理可得 :AB∥ CD所以四边形ABCD是平行四边形。由上述证明可以得到平行四边形的判定定理:两组对角分别相等的四边形是平行四边形。几何语言描述判定:∠A=∠C
∠B=∠D探究3已知:四边形ABCD中,OA=OC OB=OD,
试问:四边 形ABCD是平行四边形吗?
请说明理由。AB∥ CD , AD∥ BC△AOB≌△COD ,△AOD≌△COB要证:四边形ABCD是平行四边形∠ABO=∠CDO, ∠ DAO=∠BCO解:四边形ABCD是平行四边形。理由如下:在△ABO和△CDO中,AO=CO(已知)∠AOB=∠COD (对顶角相等)BO=DO(已知)所以△AOB≌△COD (SAS)所以 ∠ABO=∠CDO所以 AB∥ CD 所以四边形ABCD是平行四边形同理 AD∥ BC对角线互相平分的四边形是平行四边形。几何语言描述判定:AO=CO
BO=DO由上述证明可以得到平行四边形的判定定理:三、应用练习1、下面给出了四边形ABCD中 ∠A,∠B,∠C,∠D
的度数之比,其中能判定四边形ABCD是平行四边形的 是( )A.1:2:3:4 C.2:3:2:3 B.2:2:3:3 需要两组对角分别相等.D.2:3:3:2C 需要两组对边分别相等
或对角分别相等B 3、填空题:如图,
在四边形ABCD中,①如果AD=8cm,AB=4cm,且BC=___cm, CD=____cm,那么四边形ABCD是平行四边形。②若∠A=1200,则∠B=____0,∠C=____0,∠D=____0时,四边形ABCD是平行四边形。③如果AC=10cm,BD=12cm,且OA=___cm,0B=___cm,那么四边形ABCD是平行四边形。84点评:两组对边分别相等的四边形是平行四边形6012060点评:两组对角分别相等的四边形是平行四边形5点评:对角线互相平分的四边形是平行四边形6大显身手证明:因为四边形ABCD是平行四边形所以 AD ∥ BC且AD =BC所以 DE=BF所以四边形BFDE是平行四边形同理:BE=DF例、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形(两组对边分别相等的四边形是平行四边形)
例、已知:E、F是平行四边形ABCD对角线AC上的两点,
并且AE=CF。
求证:四边形BFDE是平行四边形.O证明:连接BD,交AC于点O.因为四边形ABCD是平行四边形 因为AE=CF
所以AO-AE=CO-CF即 EO=FO
又因为BO=DO
所以四边形BFDE是平行四边形.(对角线互相平分的四边形是平行四边形)
大显身手所以AO=CO,BO=DO1、已知:E、F是平行四边形ABCD对角线AC上的两点,当点E,F满足什么条件时,四边形BFDE是平行四边形?DOABCEF变式练习2、若E、F 移至OA、OC 的延长线上,且AE=CF,结论有改变吗?为什么?
变式练习 判定 1 定义:两组对边分别平行的四边形是平行四边形。 判定2 两组对边分别相等的四边形是平行四边形。 判定3 两组对角分别相等的四边形是平行四边形。 判定4 两条对角线互相平分的四边形是平行四边形。本节 课主要学习了平行四边形的判定定理:平行四边形的判别方法课本P50第5,P67第2题。作业布置新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!再 见
