2-5导数与三角函数交汇

专题 5 导数与三角函数的交汇
导数找到了三角函数，成为了指对跨阶的后花园，形成了指数、对数、三角
的三足鼎立之势，尤其在 2019全国新课标一卷的导数题出现了三角函数找点，
大家开始对导数和三角函数的交汇类型题进行疯狂研究，这一部分到底有什么秘
密呢？还是从高考原题开始研究，再通过一些最新模拟题寻找一个变化趋势，我
们尽量给到您展现那种可以触摸得到的简单。
第一讲 一切从切线开始
三角函数的切线方程，按照平移体系得到，当 0?x 时， xx ?sin ， 1cos ?x ；按照这个原理
来进行平移计算，当切点为 0xx ? 时，得到 00 )sin( xxxx ??? ， 1)cos( 0 ?? xx ；
例 1．（2019?新课标Ⅱ）曲线 2sin cosy x x? ? 在点 ( , 1)? ? 处的切线方程为 ( )
A． 1 0x y ?? ? ? ? B． 2 2 1 0x y ?? ? ? ? C． 2 2 1 0x y ?? ? ? ? D． 1 0x y ?? ? ? ?
解：法一：由 2sin cosy x x? ? ，得 2cos siny x x? ? ? ， | 2cos sin 2xy ? ? ??? ? ? ? ? ? ，
?曲线 2sin cosy x x? ? 在点 ( , 1)? ? 处的切线方程为 1 2( )y x ?? ? ? ? ，
即 2 2 1 0x y ?? ? ? ? ．故选：C．
法 二 ： xx ?sin? ， 1cos ?x ， 故 当 切 点 ??0x 时 ， 则 有
1)(2cossin2)cos()sin(2 ????????? ??? xxxxx ， 故 1)(2cossin2 ????? ?xxx ， 即
122 ???? ?xy ．故选：C．
法 三 ： 直 接 平 移 到 原 点 来 秒 杀 ， ( ) 2sin cos 2 1f x x x x?? ? ? ? ? ? ?? ，
( ) ( ) 2( ) 1f x f x x? ? ?? ? ? ? ? ? ? ? ．故选：C．
例 2．（2019?天津）曲线 cos
2
xy x? ? 在点 (0,1)处的切线方程为 ．
虽然切线方程可以通过求导直接得到，计算起来非常简单，但是通过切线得到的不等
式对解题的帮助至关重要。三角函数是一个求 n次导都没有终点的函数，通常，我们把
Rx ?? 0 ，使得 0)( 0 ??? xf 时的点 ))(( 00 xfx ， 叫做函数 )(xf 的拐点（ )(xf ?? 在 0xx ? 的两侧
异号），所以导致 0?x 时， xx sin? ， 0?x 时， xx sin? ，所以在一些解决三角函数恒成立
的问题时，通常都会给到限制范围。
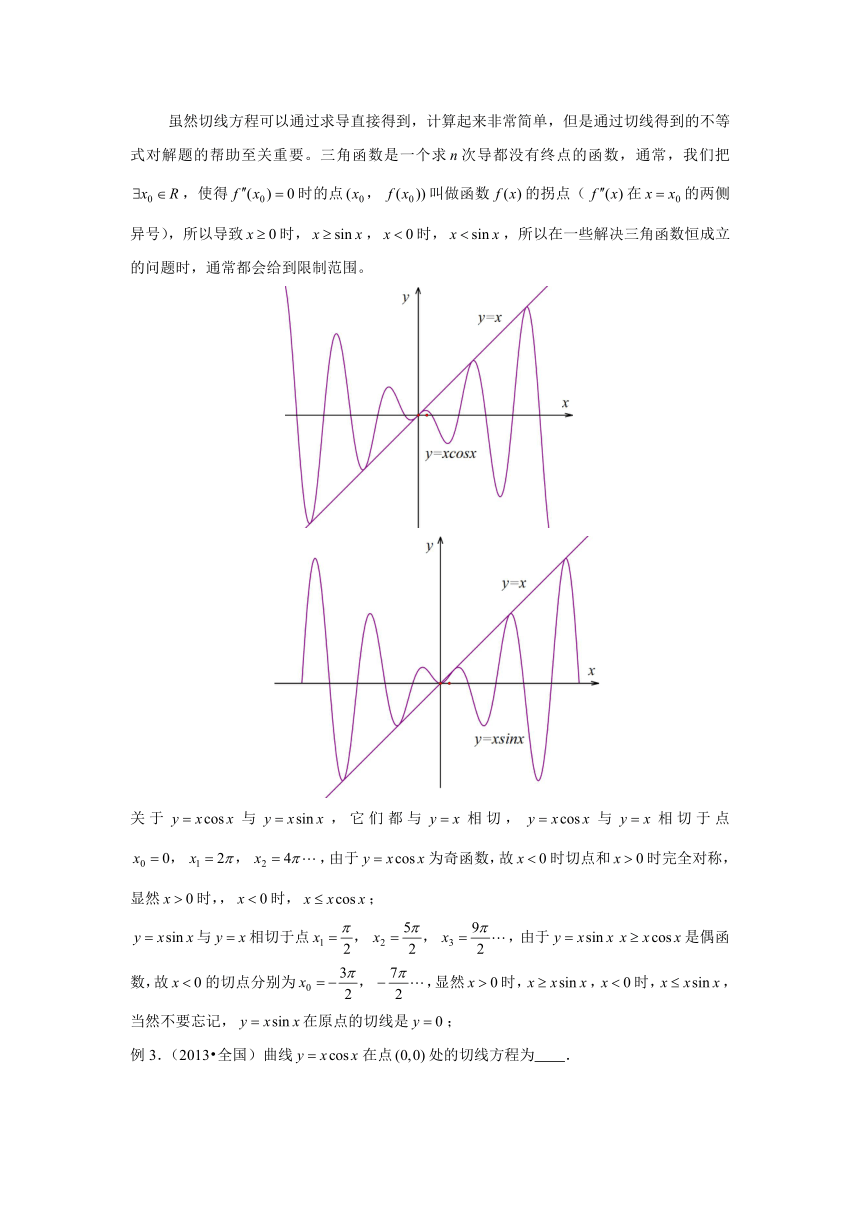
关 于 xxy cos? 与 xxy sin? ， 它 们 都 与 xy ? 相 切 ， xxy cos? 与 xy ? 相 切 于 点
??? 420 210 ??? xxx ，， ，由于 xxy cos? 为奇函数，故 0?x 时切点和 0?x 时完全对称，
显然 0?x 时，， 0?x 时， xxx cos? ；
xxy sin? 与 xy ? 相切于点 ?
2
9
2
5
2 321
???
??? xxx ，， ，由于 xxy sin? xxx cos? 是偶函
数，故 0?x 的切点分别为 ?
2
7
2
3
0
??
??? ，x ，显然 0?x 时， xxx sin? ， 0?x 时， xxx sin? ，
当然不要忘记， xxy sin? 在原点的切线是 0?y ；
例 3．（2013?全国）曲线 cosy x x? 在点 (0,0)处的切线方程为 ．
例 4．（2019?金台区月考）已知曲线 ( ) cos 3f x x x x? ? 在点 (0 ， (0))f 处的切线与直线
2 1 0ax y? ? ? 垂直，则实数 a的值为 ( )
A． 4? B． 1? C． 1
2
D．4
例 5．（2019?蚌埠期末）曲线 cosy ax x? 在
2
x ?? 处的切线与直线 2 1y x? ? 垂直，则实数 a的
值为 ( )
A． 1
?
B． 1
?
? C． 4
?
D． 4
?
?
总结：我们要的就是把这些切线的切点通过平移到原点来构造切线，先把 cosy ax x? 向左平
移
2
?
后寻找在原点位置的切线，这是一种切线的玩法。
第二讲
第三讲 三角函数中的同构式
一：找基友同构
xexh x cos)( ? ，在 )10( ， 处的切线为 1?? xy ，也可以写成 )
2
30(1cos ????? xxxe x ，
)0(1cos ??? xxxe x ；
则 xe
xxh cos)( ?? （ 如 图 ）， 它 在 )10( ， 处 的 切 线 为 1??? xy ， 也 可 以 写 成
)0
2
3(1cos ?????? xx
e
x
x ? ， )0(1
cos
???? xx
e
x
x ； xey
x cos? 与 xe
xy cos? 关于 y轴对称；
同理， xexh x sin)( ? ，在 )00( ， 处的切线为 xy ? ，也可以写成 )
4
3(sin ??? xxxe x ；
则 xe
xxh sin)( ??? （如图），它在 )00( ， 处的切线为 xy ? ，也可以写成 )
4
3(sin ???? xx
e
x
x ；
xey x sin? 与 xe
xy sin? 关于原点对称；
例 9.（2019?大理州月考）若函数 ( ) cosxf x e x? 在点 (0， (0))f 处的切线与直线 2 1 0x ay? ? ?
互相垂直，则实数 a等于 ( )
A． 2? B． 1? C．1 D．2
解：法一： ( ) cosxf x e x?? ， ( ) cos sinx xf x e x e x? ? ? ? ， 0 0(0) cos0 sin0 1f e e? ? ? ? ? ，又
函数 ( ) cosxf x e x? 在点 (0， (0))f 处的切线与直线 2 1 0x ay? ? ? 互相垂直， 21 1
a
? ? ? ? ，即
2a ? ? ．故选： A．
法二： 12)0(1cos ??????
a
xxxe x ，即 2a ? ? ．故选： A．
例 10.（2019?汉中月考）过原点作函数 sinxy e x? 的图象的切线，则切线方程是 ．
例 11.（2019?烟台期中）定义在 ( 1, )? ?? 上的函数 ( )f x 满足 ( ) cos 0f x x? ? ? ，且 (0) 1f ? ，
则不等式 ( ) sin 1f x x? ? 的解集为 ( )
A． ( ,0)?? B． ( 1,0)? C． (0, )?? D． ( 1,1)?
三．抽象函数单调性构造
关于 )(cos)('sin xxfxxf ? 或 )(sin)('cos xxfxxf ?
0)]'([sin0)(cos)('sin ???? xxfxxfxxf
当 ?
?
?
?
?
???
2
,
2
??x 0)]'([sin0)()('tan ???? xxfxfxxf
? ? ? ?( ) ( )sin cos ( ) 0 0 ; , tan ( ) 0 0
sin 2 2 sin
f x f xxf x xf x x xf x f x
x x
? ?? ?? ? ? ? ? ?? ?? ? ? ? ? ? ? ? ? ?? ?? ? ? ?? ? ? ? ? ?
当 ，
? ? ? ? ? ? ? ?
? ? ? ?
cos sin ( ) 0 cos ( ) 0 ; , tan ( ) 0 cos ( ) 0
2 2
( ) ( )cos sin ( ) 0 0 ; , tan ( ) 0 0
cos 2 2 cos
xf x xf x xf x x f x xf x xf x
f x f xxf x xf x x f x xf x
x x
? ?
? ?
? ?? ?? ?? ? ? ? ? ? ? ? ? ?? ?
? ?
? ?? ? ? ? ? ?? ?? ? ? ? ? ? ? ? ? ?? ?? ? ? ?? ? ? ? ? ?
当 ，
当 ，
口诀：正弦同号，余弦反号定理
记忆方法：看 ( )
sin
cos
x
f x
x
同号：加是乘，减是除
反号：加是除，减是乘
ì ??? ×í
???
，遇正切时化切为弦，请自己证明相
关结论．
例 15.（2019?辽源期末）定义在 (0, )
2
?
上的函数 ( )f x ， ( )f x? 是它的导函数，且恒有
( ) ( ) tanf x f x x? ? ? 成立．则有 ( )
A． 3 ( ) 2cos1 (1)
6
f f? ? ? B． 3 ( ) ( )
6 3
f f? ?? C． 2 ( ) 6 ( )
4 6
f f? ??
D． 2 ( ) ( )
4 3
f f? ??
解：当 (0, )
2
x ?? ， cos 0x ? ，则不等式 ( ) ( ) tanf x f x x? ? ? 等价为 sin( ) ( )
cos
xf x f x
x
? ? ? ，
即 cos ( ) sin ( ) 0xf x xf x? ? ? ，设 ( ) ( )cosg x f x x? ，则 ( ) cos ( ) sin ( ) 0g x xf x xf x? ? ? ? ? ，
即函数 ( )g x 在 (0, )
2
?
单调递增，因为 1
6 4 3
? ? ?
? ? ? ，所以 ( ) ( ) (1)
6 4
g g g? ?? ? ( )
3
g ?? ，
所以即
3 2( ) ( ) (1)
2 6 2 4
f f f? ?? ? 1cos1 ( )
2 3
f ?? ，即 3 ( ) 2 ( ) 2 (1)
6 4
f f f? ?? ? cos1 ( )
3
f ?? ，
故选： B．
例 16.（2019?十堰月考）设 ( )f x 是定义在 ( ,0) (0, )
2 2
? ?
? ? 上的奇函数，其导函数为 ( )f x? ，
当 (0, )
2
x ?? 时， cos( ) ( ) 0
sin
xf x f x
x
? ? ? ，则不等式
2 3( ) ( )sin
3 3
f x f x?? 的解集为 ( )
A． ( ,0) (0, )
3 3
? ?
? ? B． ( ,0) ( , )3 3 2
? ? ?
? ? C． ( , ) ( , )2 3 3 2
? ? ? ?
? ? ?
D． ( , ) (0, )
2 3 3
? ? ?
? ? ?
例 17.（2019?6 月份模拟）设奇函数 ( )f x 的定义域为 ( , )
2 2
? ?
? ，且 ( )f x 的图象是连续不间
断， ( ,0)
2
x ?? ? ? ，有 ( )cos ( )sin 0f x x f x x? ? ? ，若 ( ) 2 ( )cos
3
f m f m?? ，则m的取值范围是
( )
A． ( , )
2 3
? ?
? B． (0, )
3
? C． ( , )
2 3
? ?
? ? D． ( , )
3 2
? ?
例 18.（2020?开福区校级月考）定义在 (
2
?
? ， )
2
?
上的奇函数 ( )f x 的导函数为 ( )f x? ，且
(1)f 0? ．当 0x ? 时， ( ) tan ( ) 0f x x f x? ? ? ，则不等式 ( ) 0f x ? 的解集为 ．
第三讲 极值和最值
一．求导后需要借助辅助角公式
xbxaxf ?? cossin)( ?? ， )cossin()( cxbxaexf x ??? 或者 xe
cxbxaxf ??? cossin)( ，这类
型函数的特点就是三角函数齐次或者齐角，求完导都和辅助角公式又关联.
例 19.（2020?重庆模拟）若函数 2sin 2( ) 2cos
2
xf x x ax? ? ? 存在单调递减区间，则实数 a的
取值范團是 ( )
A． 1a B． 5a C． 1a ? D． 5a ?