冀教版六年级下册数学课件 6.3.3.可能性 (共45张PPT)
文档属性
| 名称 | 冀教版六年级下册数学课件 6.3.3.可能性 (共45张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-27 22:15:08 | ||
图片预览








文档简介
(共45张PPT)
可能性
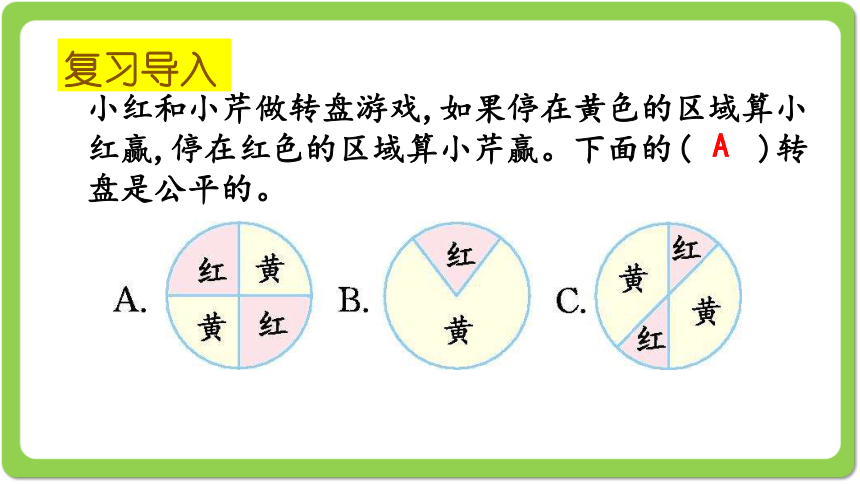
小红和小芹做转盘游戏,如果停在黄色的区域算小红赢,停在红色的区域算小芹赢。下面的( )转盘是公平的。
A
复习导入
从下面两个箱子中分别摸出1个球。
1号箱
10个红球
2号箱
5个红球,2个白球
(1)从哪个箱子中摸出的一定是红球,从哪个箱子中不一定能摸出红球?为什么?
1号箱子中全部是红球,一定能摸出红球。2号箱子有红球也有白球,可能摸出红球,也可能摸出白球。
知识梳理
从下面两个箱子中分别摸出1个球。
(2)从2号箱子中摸出哪种颜色球的可能性大?为什么?
2号箱子摸出红球的可能性大,是,白球的可能性是。
1号箱
10个红球
2号箱
5个红球,2个白球
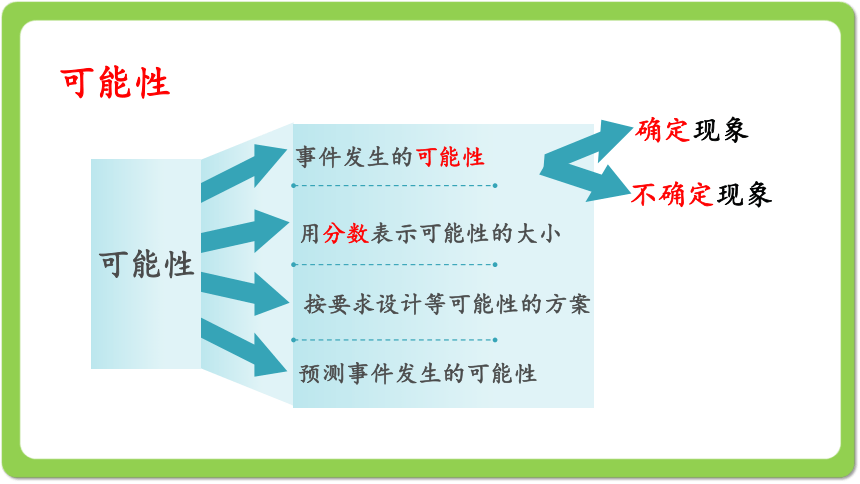
可能性
可能性
事件发生的可能性
用分数表示可能性的大小
按要求设计等可能性的方案
预测事件发生的可能性
确定现象
不确定现象
事件发生的可能性有大有小,对事件发生的可能性大小,可以用“一定”“经常”,“偶尔”
“可能”“不可能”等词语来描述。
无论在什么情况下都会发生的事件是“一定”会发生的事件;在任何情况下都不会发生的事件是“不可能”发生的事件;在某种情况下会发生,在其他情况下不会发生的事件,是“可能”发生的事件。
(1)
(2)
可能性
在可能发生的事件中,如果出现该事件的情况较多,我们就说该事件发生的可能较大;如果出现该事件的情况较少,我们就说该事件发生的可能性较小。
事件发生的可能性大小,通常用分数表示。例如,掷一枚硬币时,有正面朝上和反面朝上两种可能,那么掷一枚硬币出现正面朝上的可能性是
(1)
(2)
可能性的大小
公
平
性
游戏
公平性就是指参与游戏活动中,一个对象获胜的可能性是相等的。我们可以根据事件发生的可能性大小来设计游戏规则。当游戏双方机会均等时,游戏规则较公平;当游戏双方机会不均等时,游戏规则不公平。但当游戏双方的机会均等,游戏结果会有输赢。
游戏规则的公平性
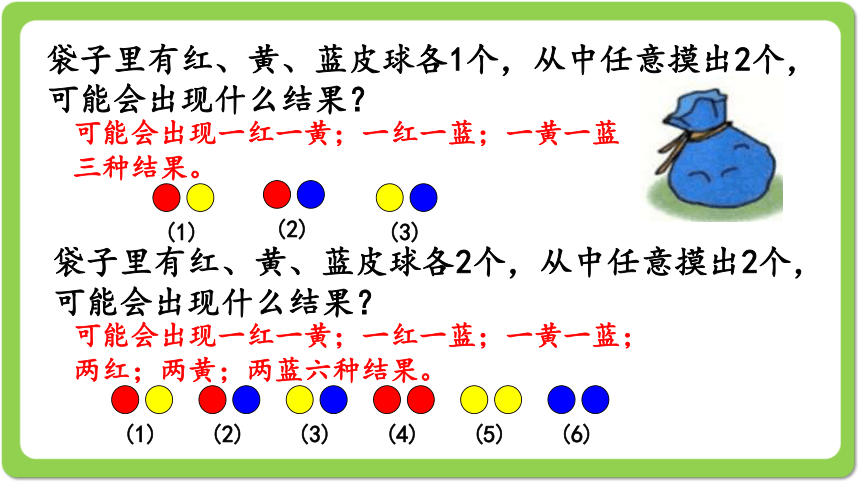
袋子里有红、黄、蓝皮球各1个,从中任意摸出2个,可能会出现什么结果?
可能会出现一红一黄;一红一蓝;一黄一蓝三种结果。
(1)
(2)
(3)
袋子里有红、黄、蓝皮球各2个,从中任意摸出2个,可能会出现什么结果?
可能会出现一红一黄;一红一蓝;一黄一蓝;两红;两黄;两蓝六种结果。
(1)
(2)
(3)
(4)
(5)
(6)
1.下列这些事情发生的可能性请选择用“可能”、“不可能”、“一定”表述。
⑴下周一会下雨。( ) ⑵太阳从西边出来。( )
⑶水在零度以下会结冰。( ) ⑷远距离投球进篮。( )
2.将扑克牌中黑桃A、红桃k、梅花A、方块J各一张放在一起,混合后从中任意取出一张,说一说:
⑴如只按字母区分,有( )种可能的结果?
⑵如只按花色区分,有( )种可能的结果?
3.学校举行篮球比赛,裁判员抛硬币来决定谁开球,出现正面的可能性与出现反面的可能性是( )的,都是( )。
可能
不可能
一定
可能
3
6
相等
任意转动指针,结果会怎样?连一连。
一定停在
涂色区域
经常停在
涂色区域
偶然停在
涂色区域
不可能停在
涂色区域
(1) (2) (3) (4)
巩固练习
在一个正八边形转盘上,按下图标出数字,在桌面上转动它。
(1)当它停止转动时,紧挨桌面的数字有几种可能?列举出来。
当它停止转动时,紧挨桌面的数字可能是1、2、3、4。
(2)哪个数字紧挨桌面的可能性最大?为什么?
在一个正八边形转盘上,按下图标出数字,在桌面上转动它。
出现3可能性大,是,出现1和2的可能性是,出现4的可能性是。
在长方形橡皮相对的面上分别标出1、2、3。抛掷橡皮,哪个面朝上的可能性最大?为什么?
提示:长方体标出1、2、3的三个面的大小不同,落地时出现的可能性大小也不同。
出现2的可能性最大。因为上下面最大且高度最矮,容易着地。
将分别标有数字1、2、3、4、5的5个小球放在盒子里。
⑴ 任意摸一个1个球,下面几种情况是“不可能发生”, 还是“一定发生”或“可能发生”?
① 球上的数是奇数; ② 球上的数小于6;
③ 球上的数大于5; ④ 球上的数不是5。
⑵ 任意摸一个球,球上的数是奇数的可能性是
摸到偶数的可能性是
1
5
4
3
2
(可能)
(一定)
(不可能)
( )
(可能)
( )。
将分别标有数字1、2、3、4、5、6的6个小球放在盒子里。
⑴ 任意摸一个1个球,下面几种情况是“不可能发生”, 还是“一定发生”或“可能发生”?
① 球上的数是奇数; ② 球上的数小于6;
③ 球上的数大于5; ④ 球上的数不是5。
1
5
4
3
2
(可能)
(可能)
6
(可能)
(可能)
⑵ 任意摸一个球,球上的数是奇数的可能性是
摸到偶数的可能性是
( )
( )。
2
2
3
3
2
2
3
3
3
3
2
2
3
3
2
2
把下面的12张牌反扣打乱,从中任意抽一张。
①抽到红桃的可能性是( )抽到其他花色的可能性是( )
②抽到“A”的可能性是( )抽到其它数字的可能性是( )
③抽到“红桃A”的可能性是( )与抽到“A”的可能性( )
2
2
3
3
2
2
3
3
3
3
2
2
3
3
2
2
按要求选牌。
①从上面的12张扑克牌中选出4张,任意抽一张,要使抽到黑桃的可能性是,可以怎样选牌?
(3张黑桃加1张其他的)
2
2
3
3
2
2
3
3
3
3
2
2
3
3
2
2
按要求选牌。
②从这些扑克牌中选出4张,任意抽一张,要使抽到梅花和方块的可能性都是 ,可以怎样选牌?
(梅花、方块各2张)
有两个相同的小正方体,它们的六个面上都分别写着1-6各数。
(1)抛掷一个小正方体,朝上的数有几种可能?
抛掷一个小正方体,朝上的数可能是1、2、3、4、5、6。
有两个相同的小正方体,它们的六个面上都分别写着1-6各数。
(2)同时抛掷两个小正方体,朝上的两个数的和最小是多少,最大是多少?
1 2 3 4 5 6
1 2
2 3
3
4
5
6
4
5
6
7
3
4
5
6
7
8
4
5
6
7
8
9
5
6
7
8
9
10
6
7
8
9
10
11
7
8
9
10
11
12
最大是12
最小是2
从结果中你发现了什么?
出现7的可能性最大,其次是6和8。
出现2和12的可能性最小。
同桌两人一起做游戏,同时抛掷两个小正方体,把两个朝上的数相加,画“正”字记录抛掷30次的结果。
两个数的和 2 3 4 5 6 7 8 9 10 11 12
出现次数
1
1
0
2
3
4
1
4
4
4
6
第6单元
第2课时 可能性
1.一枚一元的硬币掷1次,正面朝上的可能性是( ),反面朝上的可能性是( )。
一、填空题
1
2
1
2
2.在括号里填上“一定”“可能”或“不可能”。
(1)太阳( )从西边升起。
(2)明天考试小明( )得100分。
(3)三角形的内角和( )是180度。
不可能
一、填空题
可能
一定
3.盒子里装有5个红球,3个绿球,2个黄球,4个白球,任意摸一个,摸到红球的可能性是( ),摸到绿球的可能性是( ),摸到黄球的可能性是( ),摸到白球的可能性是( )。
一、填空题
5
14
3
14
1
7
2
7
4.(石家庄·期末)一副扑克牌除去大小王共有52张,任意抽取一张,抽到红桃的可能性比抽到6的可能性( )。(填“大”或“小”)
大
一、填空题
从中随机摸一个球。
二、找朋友(连一连)
1.盒子里有10个白棋子和10个黑棋子,任意摸出1个,可能是( )。
A.白棋子 B.黑棋子 C.白棋子或黑棋子
C
三、选择题
2.往下面的靶子上投飞镖,最容易投中阴影区域的是( )靶。
C
三、选择题
3.某地天气预报:明天下雨的可能性是25%,这表明( )。
A.明天不可能下雨 B.明天下雨的可能性不大
C.明天下雨的可能性较大
B
三、选择题
4.投掷一枚骰子,将其抛起落下后朝上面上的数是合数的可能性是( )。
A. B. C.
B
三、选择题
1
2
1
3
2
3
四、我会按要求涂色(任意转动指针)
【提示】 一定停在红色区域,则全涂上红色;经常停在红色区域,则红色区域涂4块或5块;偶尔停在红色区域,则红色区域涂1块或2块;不可能停在红色区域,则不涂红色。
1.这个游戏规则公平吗?为什么?
五、桌上摆着9张卡片,分别写着1~9,摸到单数佳佳赢,摸到双数悦悦赢
不公平。因为摸到单数的可能性是 ,摸到双数的可能性是 ,所以不公平。
5
9
4
9
2.佳佳一定会赢吗?
3.你能设计一个公平的游戏规则吗?
五、桌上摆着9张卡片,分别写着1~9,摸到单数佳佳赢,摸到双数悦悦赢
不一定。
去掉一个单数或增加一个双数。
六、袋子里有写着1~9的数字卡片各一张,任意摸出两张,组成一个两位数
1.如果第一张摸到5,那么组成的两位数是偶数的可能性是几分之几?是奇数的可能性是几分之几?
1
2
1
2
组成的两位数是偶数的可能性是 。
组成奇数的可能性是 。
如果第一张摸到7,那么当再摸出2或5或8时,组成的两位数是3的倍数,所以可能性是 。
六、袋子里有写着1~9的数字卡片各一张,任意摸出两张,组成一个两位数
2.如果第一张摸到7,那么组成的两位数是3的倍数的可能性是多少?
3
8
七、开动脑筋
超市为了吸引顾客,进行了一场促销活动,如图所示的是一个可以自由转动的转盘,顾客消费满100元就可获得一次转动转盘的机会。转盘停止后,指针对着哪个区域,就享受相应的打折优惠。
她享受打折的机会为 ,
七、开动脑筋
1.王阿姨消费120元,她享受打折的机会有多大?获得八折、七折的可能性分别是多少?
3
8
1
8
1
8
获得八折的可能性为 ,
获得七折的可能性为 。
因为消费满100元可获得打折机会,所以他获得打折的可能性为0。
七、开动脑筋
2.张叔叔消费95元,他获得打折的可能性是多少?
琪琪赢的可能性大
八、解决问题
1.桌子上有3张数字卡片,分别写着7,8,9,若摆出的三位数是奇数,则琪琪赢,若摆出的三位数是偶数,则悦悦赢,想一想,谁赢的可能性大?
10×9÷2=45(场)
八、解决问题
2.六(1)班共10名同学进行乒乓球比赛,若每2名同学之间都要进行一场比赛,则一共要比赛多少场?
答:一共要比赛45场。
看
谢
谢
观
可能性
小红和小芹做转盘游戏,如果停在黄色的区域算小红赢,停在红色的区域算小芹赢。下面的( )转盘是公平的。
A
复习导入
从下面两个箱子中分别摸出1个球。
1号箱
10个红球
2号箱
5个红球,2个白球
(1)从哪个箱子中摸出的一定是红球,从哪个箱子中不一定能摸出红球?为什么?
1号箱子中全部是红球,一定能摸出红球。2号箱子有红球也有白球,可能摸出红球,也可能摸出白球。
知识梳理
从下面两个箱子中分别摸出1个球。
(2)从2号箱子中摸出哪种颜色球的可能性大?为什么?
2号箱子摸出红球的可能性大,是,白球的可能性是。
1号箱
10个红球
2号箱
5个红球,2个白球
可能性
可能性
事件发生的可能性
用分数表示可能性的大小
按要求设计等可能性的方案
预测事件发生的可能性
确定现象
不确定现象
事件发生的可能性有大有小,对事件发生的可能性大小,可以用“一定”“经常”,“偶尔”
“可能”“不可能”等词语来描述。
无论在什么情况下都会发生的事件是“一定”会发生的事件;在任何情况下都不会发生的事件是“不可能”发生的事件;在某种情况下会发生,在其他情况下不会发生的事件,是“可能”发生的事件。
(1)
(2)
可能性
在可能发生的事件中,如果出现该事件的情况较多,我们就说该事件发生的可能较大;如果出现该事件的情况较少,我们就说该事件发生的可能性较小。
事件发生的可能性大小,通常用分数表示。例如,掷一枚硬币时,有正面朝上和反面朝上两种可能,那么掷一枚硬币出现正面朝上的可能性是
(1)
(2)
可能性的大小
公
平
性
游戏
公平性就是指参与游戏活动中,一个对象获胜的可能性是相等的。我们可以根据事件发生的可能性大小来设计游戏规则。当游戏双方机会均等时,游戏规则较公平;当游戏双方机会不均等时,游戏规则不公平。但当游戏双方的机会均等,游戏结果会有输赢。
游戏规则的公平性
袋子里有红、黄、蓝皮球各1个,从中任意摸出2个,可能会出现什么结果?
可能会出现一红一黄;一红一蓝;一黄一蓝三种结果。
(1)
(2)
(3)
袋子里有红、黄、蓝皮球各2个,从中任意摸出2个,可能会出现什么结果?
可能会出现一红一黄;一红一蓝;一黄一蓝;两红;两黄;两蓝六种结果。
(1)
(2)
(3)
(4)
(5)
(6)
1.下列这些事情发生的可能性请选择用“可能”、“不可能”、“一定”表述。
⑴下周一会下雨。( ) ⑵太阳从西边出来。( )
⑶水在零度以下会结冰。( ) ⑷远距离投球进篮。( )
2.将扑克牌中黑桃A、红桃k、梅花A、方块J各一张放在一起,混合后从中任意取出一张,说一说:
⑴如只按字母区分,有( )种可能的结果?
⑵如只按花色区分,有( )种可能的结果?
3.学校举行篮球比赛,裁判员抛硬币来决定谁开球,出现正面的可能性与出现反面的可能性是( )的,都是( )。
可能
不可能
一定
可能
3
6
相等
任意转动指针,结果会怎样?连一连。
一定停在
涂色区域
经常停在
涂色区域
偶然停在
涂色区域
不可能停在
涂色区域
(1) (2) (3) (4)
巩固练习
在一个正八边形转盘上,按下图标出数字,在桌面上转动它。
(1)当它停止转动时,紧挨桌面的数字有几种可能?列举出来。
当它停止转动时,紧挨桌面的数字可能是1、2、3、4。
(2)哪个数字紧挨桌面的可能性最大?为什么?
在一个正八边形转盘上,按下图标出数字,在桌面上转动它。
出现3可能性大,是,出现1和2的可能性是,出现4的可能性是。
在长方形橡皮相对的面上分别标出1、2、3。抛掷橡皮,哪个面朝上的可能性最大?为什么?
提示:长方体标出1、2、3的三个面的大小不同,落地时出现的可能性大小也不同。
出现2的可能性最大。因为上下面最大且高度最矮,容易着地。
将分别标有数字1、2、3、4、5的5个小球放在盒子里。
⑴ 任意摸一个1个球,下面几种情况是“不可能发生”, 还是“一定发生”或“可能发生”?
① 球上的数是奇数; ② 球上的数小于6;
③ 球上的数大于5; ④ 球上的数不是5。
⑵ 任意摸一个球,球上的数是奇数的可能性是
摸到偶数的可能性是
1
5
4
3
2
(可能)
(一定)
(不可能)
( )
(可能)
( )。
将分别标有数字1、2、3、4、5、6的6个小球放在盒子里。
⑴ 任意摸一个1个球,下面几种情况是“不可能发生”, 还是“一定发生”或“可能发生”?
① 球上的数是奇数; ② 球上的数小于6;
③ 球上的数大于5; ④ 球上的数不是5。
1
5
4
3
2
(可能)
(可能)
6
(可能)
(可能)
⑵ 任意摸一个球,球上的数是奇数的可能性是
摸到偶数的可能性是
( )
( )。
2
2
3
3
2
2
3
3
3
3
2
2
3
3
2
2
把下面的12张牌反扣打乱,从中任意抽一张。
①抽到红桃的可能性是( )抽到其他花色的可能性是( )
②抽到“A”的可能性是( )抽到其它数字的可能性是( )
③抽到“红桃A”的可能性是( )与抽到“A”的可能性( )
2
2
3
3
2
2
3
3
3
3
2
2
3
3
2
2
按要求选牌。
①从上面的12张扑克牌中选出4张,任意抽一张,要使抽到黑桃的可能性是,可以怎样选牌?
(3张黑桃加1张其他的)
2
2
3
3
2
2
3
3
3
3
2
2
3
3
2
2
按要求选牌。
②从这些扑克牌中选出4张,任意抽一张,要使抽到梅花和方块的可能性都是 ,可以怎样选牌?
(梅花、方块各2张)
有两个相同的小正方体,它们的六个面上都分别写着1-6各数。
(1)抛掷一个小正方体,朝上的数有几种可能?
抛掷一个小正方体,朝上的数可能是1、2、3、4、5、6。
有两个相同的小正方体,它们的六个面上都分别写着1-6各数。
(2)同时抛掷两个小正方体,朝上的两个数的和最小是多少,最大是多少?
1 2 3 4 5 6
1 2
2 3
3
4
5
6
4
5
6
7
3
4
5
6
7
8
4
5
6
7
8
9
5
6
7
8
9
10
6
7
8
9
10
11
7
8
9
10
11
12
最大是12
最小是2
从结果中你发现了什么?
出现7的可能性最大,其次是6和8。
出现2和12的可能性最小。
同桌两人一起做游戏,同时抛掷两个小正方体,把两个朝上的数相加,画“正”字记录抛掷30次的结果。
两个数的和 2 3 4 5 6 7 8 9 10 11 12
出现次数
1
1
0
2
3
4
1
4
4
4
6
第6单元
第2课时 可能性
1.一枚一元的硬币掷1次,正面朝上的可能性是( ),反面朝上的可能性是( )。
一、填空题
1
2
1
2
2.在括号里填上“一定”“可能”或“不可能”。
(1)太阳( )从西边升起。
(2)明天考试小明( )得100分。
(3)三角形的内角和( )是180度。
不可能
一、填空题
可能
一定
3.盒子里装有5个红球,3个绿球,2个黄球,4个白球,任意摸一个,摸到红球的可能性是( ),摸到绿球的可能性是( ),摸到黄球的可能性是( ),摸到白球的可能性是( )。
一、填空题
5
14
3
14
1
7
2
7
4.(石家庄·期末)一副扑克牌除去大小王共有52张,任意抽取一张,抽到红桃的可能性比抽到6的可能性( )。(填“大”或“小”)
大
一、填空题
从中随机摸一个球。
二、找朋友(连一连)
1.盒子里有10个白棋子和10个黑棋子,任意摸出1个,可能是( )。
A.白棋子 B.黑棋子 C.白棋子或黑棋子
C
三、选择题
2.往下面的靶子上投飞镖,最容易投中阴影区域的是( )靶。
C
三、选择题
3.某地天气预报:明天下雨的可能性是25%,这表明( )。
A.明天不可能下雨 B.明天下雨的可能性不大
C.明天下雨的可能性较大
B
三、选择题
4.投掷一枚骰子,将其抛起落下后朝上面上的数是合数的可能性是( )。
A. B. C.
B
三、选择题
1
2
1
3
2
3
四、我会按要求涂色(任意转动指针)
【提示】 一定停在红色区域,则全涂上红色;经常停在红色区域,则红色区域涂4块或5块;偶尔停在红色区域,则红色区域涂1块或2块;不可能停在红色区域,则不涂红色。
1.这个游戏规则公平吗?为什么?
五、桌上摆着9张卡片,分别写着1~9,摸到单数佳佳赢,摸到双数悦悦赢
不公平。因为摸到单数的可能性是 ,摸到双数的可能性是 ,所以不公平。
5
9
4
9
2.佳佳一定会赢吗?
3.你能设计一个公平的游戏规则吗?
五、桌上摆着9张卡片,分别写着1~9,摸到单数佳佳赢,摸到双数悦悦赢
不一定。
去掉一个单数或增加一个双数。
六、袋子里有写着1~9的数字卡片各一张,任意摸出两张,组成一个两位数
1.如果第一张摸到5,那么组成的两位数是偶数的可能性是几分之几?是奇数的可能性是几分之几?
1
2
1
2
组成的两位数是偶数的可能性是 。
组成奇数的可能性是 。
如果第一张摸到7,那么当再摸出2或5或8时,组成的两位数是3的倍数,所以可能性是 。
六、袋子里有写着1~9的数字卡片各一张,任意摸出两张,组成一个两位数
2.如果第一张摸到7,那么组成的两位数是3的倍数的可能性是多少?
3
8
七、开动脑筋
超市为了吸引顾客,进行了一场促销活动,如图所示的是一个可以自由转动的转盘,顾客消费满100元就可获得一次转动转盘的机会。转盘停止后,指针对着哪个区域,就享受相应的打折优惠。
她享受打折的机会为 ,
七、开动脑筋
1.王阿姨消费120元,她享受打折的机会有多大?获得八折、七折的可能性分别是多少?
3
8
1
8
1
8
获得八折的可能性为 ,
获得七折的可能性为 。
因为消费满100元可获得打折机会,所以他获得打折的可能性为0。
七、开动脑筋
2.张叔叔消费95元,他获得打折的可能性是多少?
琪琪赢的可能性大
八、解决问题
1.桌子上有3张数字卡片,分别写着7,8,9,若摆出的三位数是奇数,则琪琪赢,若摆出的三位数是偶数,则悦悦赢,想一想,谁赢的可能性大?
10×9÷2=45(场)
八、解决问题
2.六(1)班共10名同学进行乒乓球比赛,若每2名同学之间都要进行一场比赛,则一共要比赛多少场?
答:一共要比赛45场。
看
谢
谢
观
