人教版九年级数学下册 27.2.2 相似三角形的性质 同步练习(含答案)
文档属性
| 名称 | 人教版九年级数学下册 27.2.2 相似三角形的性质 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 246.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-28 06:57:42 | ||
图片预览

文档简介
27.2.2相似三角形的性质
同步练习
选择题
1.把一个三角形改成和它相似的三角形,如果面积扩大到原来的100倍,那么边长扩大到原来的( )
A.10000倍 B.10倍 C.100倍 D.1000倍
如图,已知DE//BC,CD和BE相交于点O,,则AE:EC为( )
?A. B. C. D.
3.已知两个五边形相似,其中一个五边形的周长为36,最短边长为4,另一个五边形的最短边长为3,则它的周长为( )
A.21 B.27 C.30 D.48
4.在△ABC中,D,E分别为边AB,AC的中点,则△ADE与△ABC的面积之比为( )
A. B. C. D.
5.如图,在?ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为,则下列结论中正确的是( )
A.m=5 B.m=4 C.m=3 D.m=10
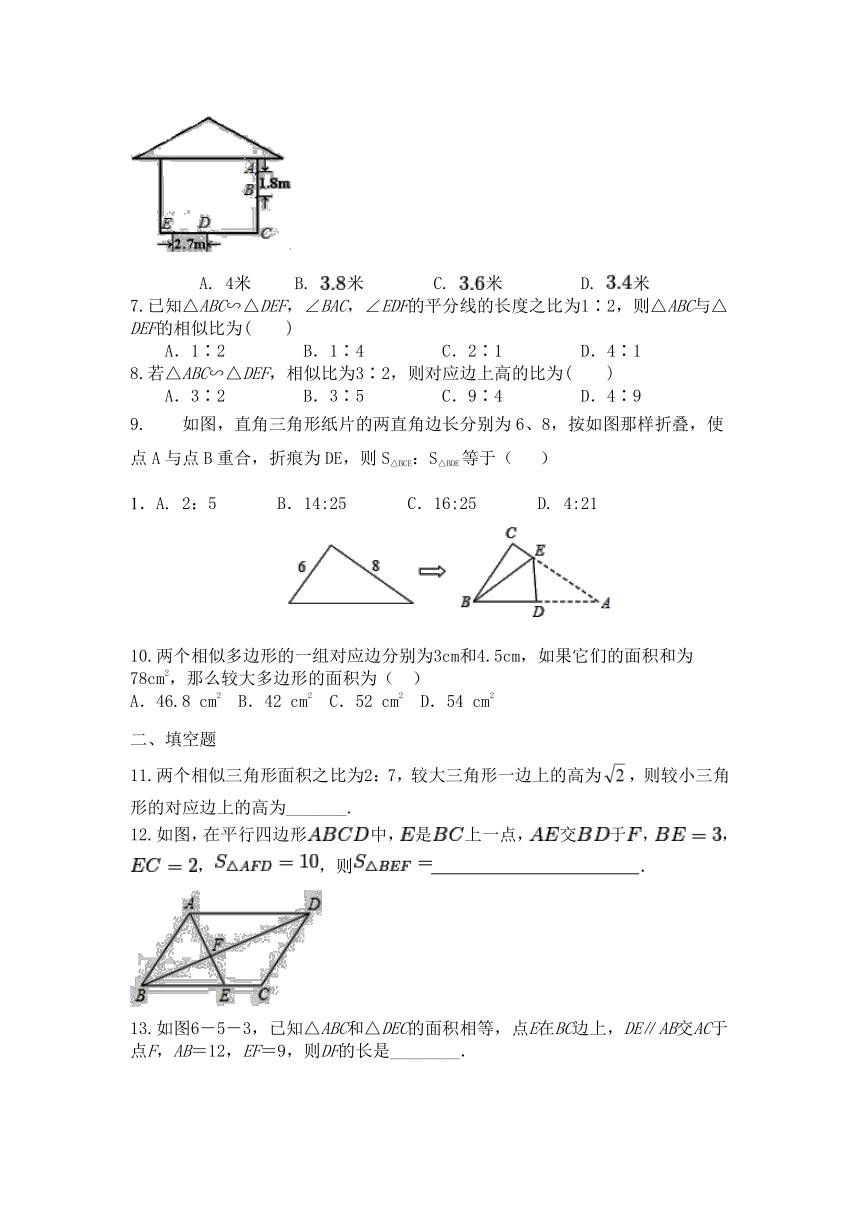
6.阳光通过窗口照射到室内,在地面上留下米的亮区(如图所示),已知亮区到窗口下的墙角的距离米,窗口高米,则窗口底边离地面的高为( )
????A. 4米 B. 米 ?C. 米 ?D. 米
7.已知△ABC∽△DEF,∠BAC,∠EDF的平分线的长度之比为1∶2,则△ABC与△DEF的相似比为( )
A.1∶2 B.1∶4 C.2∶1 D.4∶1
8.若△ABC∽△DEF,相似比为3∶2,则对应边上高的比为( )
A.3∶2 B.3∶5 C.9∶4 D.4∶9
如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )
A. 2:5 B.14:25 C.16:25 D. 4:21
10.两个相似多边形的一组对应边分别为3cm和4.5cm,如果它们的面积和为78cm2,那么较大多边形的面积为( )
A.46.8 cm2 B.42 cm2 C.52 cm2 D.54 cm2
填空题
11.两个相似三角形面积之比为2:7,较大三角形一边上的高为,则较小三角形的对应边上的高为_______.
12.如图,在平行四边形中,是上一点,交于,,,,则????????????.
13.如图6-5-3,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是________.
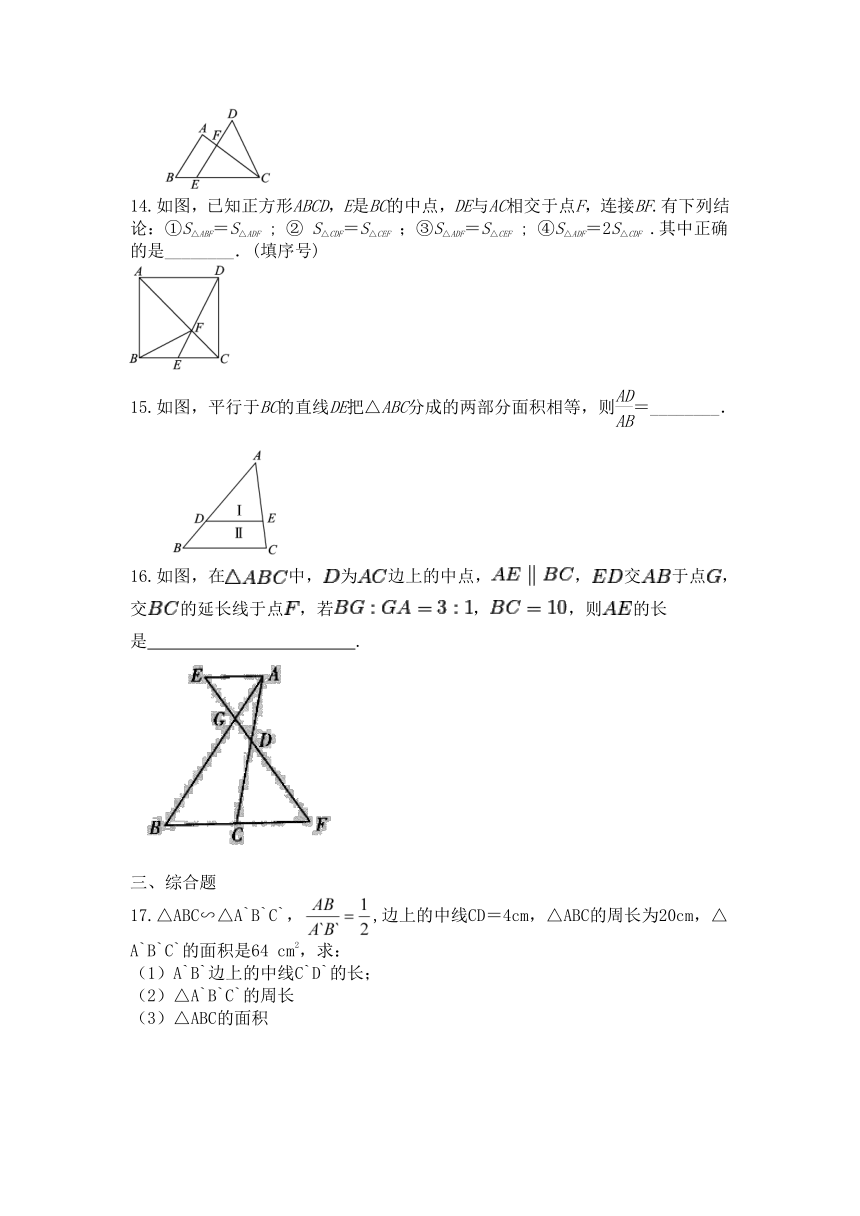
14.如图,已知正方形ABCD,E是BC的中点,DE与AC相交于点F,连接BF.有下列结论:①S△ABF=S△ADF ; ② S△CDF=S△CEF ;③S△ADF=S△CEF ; ④S△ADF=2S△CDF .其中正确的是________.(填序号)
15.如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则=________.
16.如图,在中,为边上的中点,,交于点,交的延长线于点,若,,则的长是????????????.
综合题
17.△ABC∽△A`B`C`,,边上的中线CD=4cm,△ABC的周长为20cm,△A`B`C`的面积是64 cm2,求:
(1)A`B`边上的中线C`D`的长;
(2)△A`B`C`的周长
(3)△ABC的面积
如图,在矩形中,已知,,、分别是、上的点,且,两动点、分别从、两点,同时出发沿、且均以速度分别向、运动,猜想当、运动多长时间时矩形与矩形相似?写出你的猜想过程.
19.如图,已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的点P处.已知折痕与边BC交于点O.
(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1∶4,求边AB的长.
20.如图,在△ABC中,D,E分别是AB,AC上的点,△ADE∽△ACB,相似比为AD∶AC=2∶3,△ABC的角平分线AF交DE于点G,交BC于点F,求AG与GF的比.
27.2.2 相似三角形的性质
同步练习
选择题
1.B 2.D 3.B 4.C 5.B 6.A 7.A 8.A 9.B 10.D
二、填空题
11.
12.18/5
13.7
14. ①④
15.
16.5
三、综合
17.(1)C?D?=8cm;(2)△A?B?C?的周长为80cm;(3)△ABC的面积为16cm2。
18.解:设运动时间是t秒,那么.
,,
由矩形可得,.
,
.
当矩形与矩形相似时,就有,或者.
,或者.
(秒),或者(秒).
故当、运动秒或秒长的时间时,矩形与矩形相似.
19.解:(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
∴∠CPO+∠COP=90°.
由折叠的性质可得,∠APO=∠B=90°,
∴∠CPO+∠DPA=90°,∴∠COP=∠DPA,
∴△OCP∽△PDA.
(2)∵△OCP与△PDA的面积比为1∶4,△OCP∽△PDA,
∴===,
∴PA=2OP,AD=2PC.
∵AD=8,∴PC=4.
由折叠的性质可得OP=OB,PA=AB.
设OP=x,则OB=x,CO=8-x.
在Rt△PCO中,
∵∠C=90°,PC=4,OP=x,CO=8-x,
∴x2=(8-x)2+42,解得x=5,则OP=5,
∴AB=AP=2OP=10.
20.解:∵△ABC的角平分线AF交DE于点G,
∴AG是△ADE的角平分线.
∵△ADE∽△ACB,
∴AG∶AF=AD∶AC=2∶3,
∴AG∶GF=2∶1.
同步练习
选择题
1.把一个三角形改成和它相似的三角形,如果面积扩大到原来的100倍,那么边长扩大到原来的( )
A.10000倍 B.10倍 C.100倍 D.1000倍
如图,已知DE//BC,CD和BE相交于点O,,则AE:EC为( )
?A. B. C. D.
3.已知两个五边形相似,其中一个五边形的周长为36,最短边长为4,另一个五边形的最短边长为3,则它的周长为( )
A.21 B.27 C.30 D.48
4.在△ABC中,D,E分别为边AB,AC的中点,则△ADE与△ABC的面积之比为( )
A. B. C. D.
5.如图,在?ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为,则下列结论中正确的是( )
A.m=5 B.m=4 C.m=3 D.m=10
6.阳光通过窗口照射到室内,在地面上留下米的亮区(如图所示),已知亮区到窗口下的墙角的距离米,窗口高米,则窗口底边离地面的高为( )
????A. 4米 B. 米 ?C. 米 ?D. 米
7.已知△ABC∽△DEF,∠BAC,∠EDF的平分线的长度之比为1∶2,则△ABC与△DEF的相似比为( )
A.1∶2 B.1∶4 C.2∶1 D.4∶1
8.若△ABC∽△DEF,相似比为3∶2,则对应边上高的比为( )
A.3∶2 B.3∶5 C.9∶4 D.4∶9
如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )
A. 2:5 B.14:25 C.16:25 D. 4:21
10.两个相似多边形的一组对应边分别为3cm和4.5cm,如果它们的面积和为78cm2,那么较大多边形的面积为( )
A.46.8 cm2 B.42 cm2 C.52 cm2 D.54 cm2
填空题
11.两个相似三角形面积之比为2:7,较大三角形一边上的高为,则较小三角形的对应边上的高为_______.
12.如图,在平行四边形中,是上一点,交于,,,,则????????????.
13.如图6-5-3,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是________.
14.如图,已知正方形ABCD,E是BC的中点,DE与AC相交于点F,连接BF.有下列结论:①S△ABF=S△ADF ; ② S△CDF=S△CEF ;③S△ADF=S△CEF ; ④S△ADF=2S△CDF .其中正确的是________.(填序号)
15.如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则=________.
16.如图,在中,为边上的中点,,交于点,交的延长线于点,若,,则的长是????????????.
综合题
17.△ABC∽△A`B`C`,,边上的中线CD=4cm,△ABC的周长为20cm,△A`B`C`的面积是64 cm2,求:
(1)A`B`边上的中线C`D`的长;
(2)△A`B`C`的周长
(3)△ABC的面积
如图,在矩形中,已知,,、分别是、上的点,且,两动点、分别从、两点,同时出发沿、且均以速度分别向、运动,猜想当、运动多长时间时矩形与矩形相似?写出你的猜想过程.
19.如图,已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的点P处.已知折痕与边BC交于点O.
(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1∶4,求边AB的长.
20.如图,在△ABC中,D,E分别是AB,AC上的点,△ADE∽△ACB,相似比为AD∶AC=2∶3,△ABC的角平分线AF交DE于点G,交BC于点F,求AG与GF的比.
27.2.2 相似三角形的性质
同步练习
选择题
1.B 2.D 3.B 4.C 5.B 6.A 7.A 8.A 9.B 10.D
二、填空题
11.
12.18/5
13.7
14. ①④
15.
16.5
三、综合
17.(1)C?D?=8cm;(2)△A?B?C?的周长为80cm;(3)△ABC的面积为16cm2。
18.解:设运动时间是t秒,那么.
,,
由矩形可得,.
,
.
当矩形与矩形相似时,就有,或者.
,或者.
(秒),或者(秒).
故当、运动秒或秒长的时间时,矩形与矩形相似.
19.解:(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠D=90°,
∴∠CPO+∠COP=90°.
由折叠的性质可得,∠APO=∠B=90°,
∴∠CPO+∠DPA=90°,∴∠COP=∠DPA,
∴△OCP∽△PDA.
(2)∵△OCP与△PDA的面积比为1∶4,△OCP∽△PDA,
∴===,
∴PA=2OP,AD=2PC.
∵AD=8,∴PC=4.
由折叠的性质可得OP=OB,PA=AB.
设OP=x,则OB=x,CO=8-x.
在Rt△PCO中,
∵∠C=90°,PC=4,OP=x,CO=8-x,
∴x2=(8-x)2+42,解得x=5,则OP=5,
∴AB=AP=2OP=10.
20.解:∵△ABC的角平分线AF交DE于点G,
∴AG是△ADE的角平分线.
∵△ADE∽△ACB,
∴AG∶AF=AD∶AC=2∶3,
∴AG∶GF=2∶1.
