苏科版七年级下册10.4 三元一次方程组 课件(13张)
文档属性
| 名称 | 苏科版七年级下册10.4 三元一次方程组 课件(13张) |  | |
| 格式 | zip | ||
| 文件大小 | 576.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-28 07:41:13 | ||
图片预览





文档简介
(共13张PPT)
10.4 解三元一次方程组
(选学内容)
【学习目标】
1.了解三元一次方程(组)的含义.
2.会用代入法或加减法解简单的三元一次方程组.
3.体会解三元一次方程组的思想“消元”,即将“三元”化为“二元”或“一元”的思想.
【新知导入】
足球比赛规定:胜一场得3分,平一场得1分,负一场得0分.某足球队赛了22场得47分,且胜的场数比负的场数的4倍还多2.求球队胜、平、负各几场?
x+y+z=22
3x+y=47
x=4z+2
解:设该球队胜x场,平y场,负z场:
定义:含有三个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做三元一次方程.
题中的三个条件要同时满足,所以我们把三个方程合在一起写成 :
三元一次方程组:
含有三个相同的未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
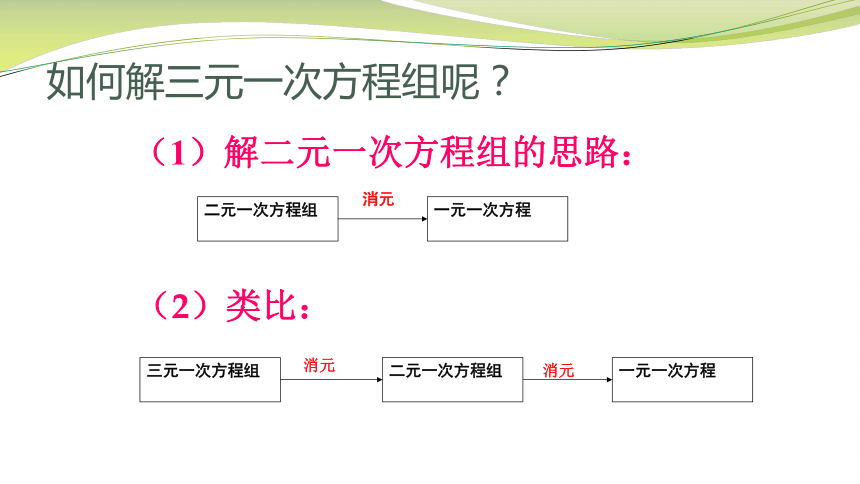
(1)解二元一次方程组的思路:
(2)类比:
消元
消元
如何解三元一次方程组呢?
①
②
③
解:②-①得:2x-z=25 ④
把x=14,代入②,得:y=5
加减法
代入法
分析:方程①中只含x,z,因此,可以由②③消去y,得到一个只含x,z的方程,与方程①组成一个二元一次方程组.
例1
解:②×3+③ ,得11x+10z=35 ④
①与④联立:
解得
把x=5,z=-2代入②,得y=
则方程组的解为
①
③
②
解:①+②,得 5x+2y=16 ④
②+③, 得 3x+4y=18 ⑤
④
⑤
把x=2,y=3 代入③,得 z=1
“消元”的关键:选准先消去的未知数.
原则:①消去系数最简单的未知数;
②消去某个方程中缺少的未知数;
③消去系数成整倍数关系的未知数;在整个“消元”过程中,必须保证每个方程至少用一次。
注意点:要选方程,它与其他两个方程消去同一个未知数,被选用的方程一般用2次.
例2
例3 在等式 y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60. 求a,b,c的值.
解:根据题意,得:
a-b+c= 0 ①
4a+2b+c=3 ②
25a+5b+c=60 ③
②-①, 得 a+b=1 ④
③-①,得 4a+b=10 ⑤
④与⑤组成二元一次方程组
a+b=1,
4a+b=10.
a=3,
b=-2.
解这个方程组,得
把 代入①,得
a=3,
b=-2.
c=-5
a=3,
b=-2,
c=-5.
所以
巩固练习
解三元一次方程组的基本思路是:通过“代入法”或“加减法”进行消元,把“三元”化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
在你内心深处,
还有无穷的潜力!
祝同学们学业进步,身体健康!!
10.4 解三元一次方程组
(选学内容)
【学习目标】
1.了解三元一次方程(组)的含义.
2.会用代入法或加减法解简单的三元一次方程组.
3.体会解三元一次方程组的思想“消元”,即将“三元”化为“二元”或“一元”的思想.
【新知导入】
足球比赛规定:胜一场得3分,平一场得1分,负一场得0分.某足球队赛了22场得47分,且胜的场数比负的场数的4倍还多2.求球队胜、平、负各几场?
x+y+z=22
3x+y=47
x=4z+2
解:设该球队胜x场,平y场,负z场:
定义:含有三个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做三元一次方程.
题中的三个条件要同时满足,所以我们把三个方程合在一起写成 :
三元一次方程组:
含有三个相同的未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
(1)解二元一次方程组的思路:
(2)类比:
消元
消元
如何解三元一次方程组呢?
①
②
③
解:②-①得:2x-z=25 ④
把x=14,代入②,得:y=5
加减法
代入法
分析:方程①中只含x,z,因此,可以由②③消去y,得到一个只含x,z的方程,与方程①组成一个二元一次方程组.
例1
解:②×3+③ ,得11x+10z=35 ④
①与④联立:
解得
把x=5,z=-2代入②,得y=
则方程组的解为
①
③
②
解:①+②,得 5x+2y=16 ④
②+③, 得 3x+4y=18 ⑤
④
⑤
把x=2,y=3 代入③,得 z=1
“消元”的关键:选准先消去的未知数.
原则:①消去系数最简单的未知数;
②消去某个方程中缺少的未知数;
③消去系数成整倍数关系的未知数;在整个“消元”过程中,必须保证每个方程至少用一次。
注意点:要选方程,它与其他两个方程消去同一个未知数,被选用的方程一般用2次.
例2
例3 在等式 y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60. 求a,b,c的值.
解:根据题意,得:
a-b+c= 0 ①
4a+2b+c=3 ②
25a+5b+c=60 ③
②-①, 得 a+b=1 ④
③-①,得 4a+b=10 ⑤
④与⑤组成二元一次方程组
a+b=1,
4a+b=10.
a=3,
b=-2.
解这个方程组,得
把 代入①,得
a=3,
b=-2.
c=-5
a=3,
b=-2,
c=-5.
所以
巩固练习
解三元一次方程组的基本思路是:通过“代入法”或“加减法”进行消元,把“三元”化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
在你内心深处,
还有无穷的潜力!
祝同学们学业进步,身体健康!!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
