人教版八年级数学下册18.2.1矩形的性质(第1课时)课件(共21张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.2.1矩形的性质(第1课时)课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 141.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-28 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
人教版八年级数学
第十八章 平行四边形
18.2.1矩形的性质(第一课时)
课标解读
1.理解矩形的定义,能够把矩形的定义作为性质和判定进行运用。
2.掌握矩形的性质定理,并能灵活运用这些性质定理解决问题。
3.理解并掌握直角三角形斜边上的中线的性质,并能利用这一性质进行有关的计算和证明。
知识梳理
1.矩形的定义:有一个角是直角的平行四边形是矩形,也称为长方形
温馨提示:矩形的定义有两个要素:
①四边形是平行四边形
②有一个角是直角,二者缺一不可。
A
B
C
D
矩形是特殊的平行四边形,因此它具有平行四边形的所有性质,但它也有自己独特的性质。
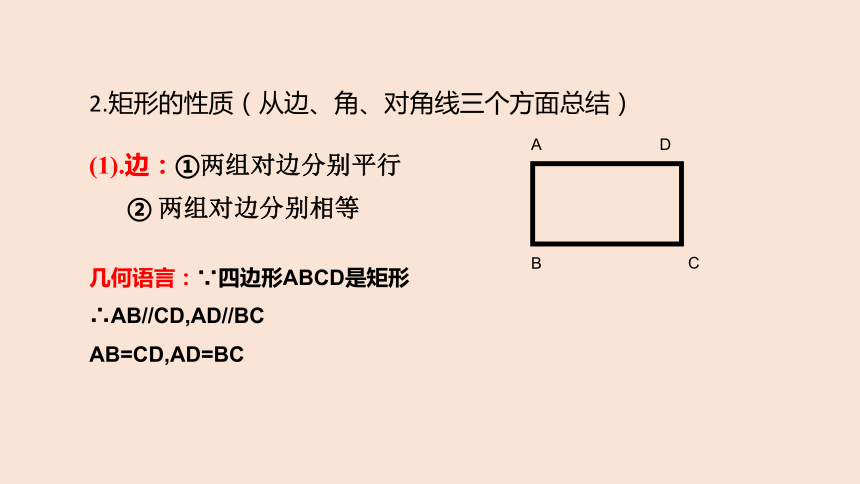
2.矩形的性质(从边、角、对角线三个方面总结)
(1).边:①两组对边分别平行
② 两组对边分别相等
A
B
C
D
几何语言:∵四边形ABCD是矩形
∴AB//CD,AD//BC
AB=CD,AD=BC
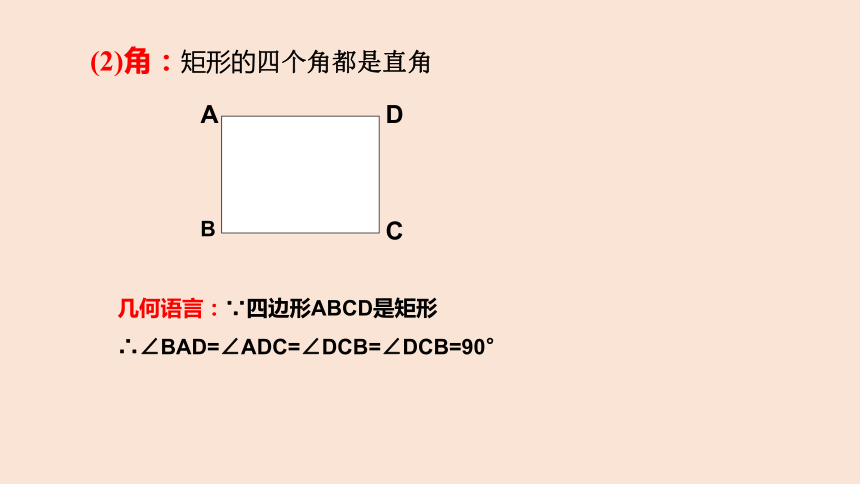
(2)角:矩形的四个角都是直角
A
B
C
D
几何语言:∵四边形ABCD是矩形
∴∠BAD=∠ADC=∠DCB=∠DCB=90°
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,
求证:∠A=∠B=∠C=∠D=90°.
A
B
C
D
证明: ∵四边形ABCD是矩形,
∴ ∠A=90°.
又 矩形ABCD是平行四边形,
∴ ∠A=∠C ∠B = ∠D.
∠A +∠B = 90°.
∴ ∠A=∠B=∠C=∠D=90°,
即矩形的四个角都是直角.
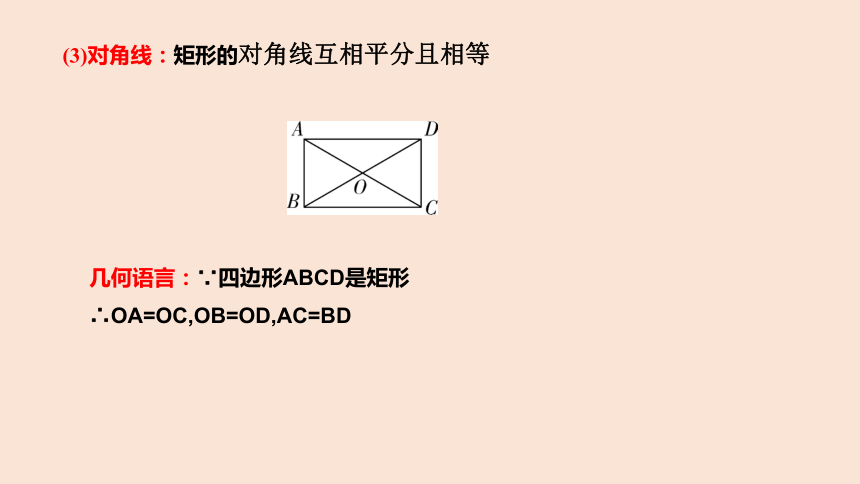
(3)对角线:矩形的对角线互相平分且相等
几何语言:∵四边形ABCD是矩形
∴OA=OC,OB=OD,AC=BD
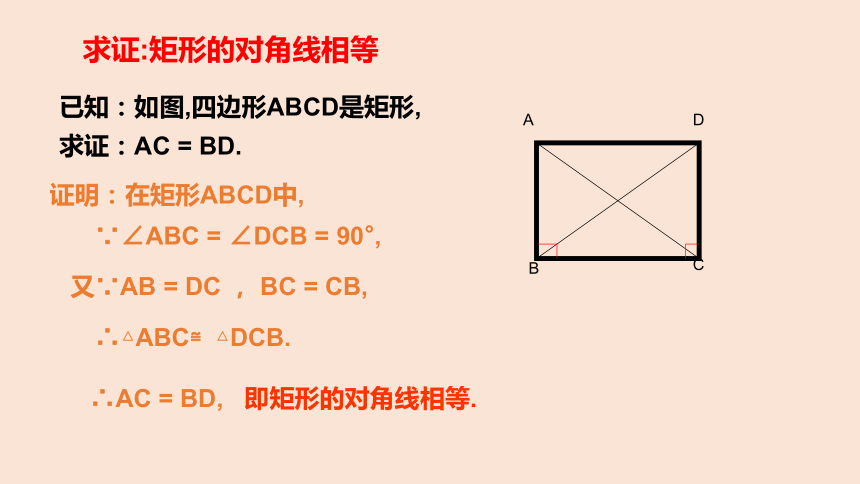
已知:如图,四边形ABCD是矩形,
求证:AC = BD.
A
B
C
D
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
又∵AB = DC , BC = CB,
∴△ABC≌△DCB.
∴AC = BD, 即矩形的对角线相等.
求证:矩形的对角线相等
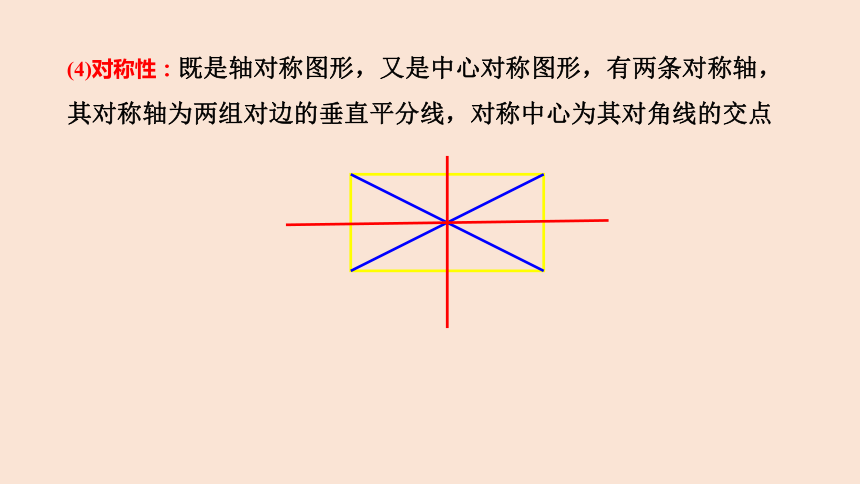
(4)对称性:既是轴对称图形,又是中心对称图形,有两条对称轴,其对称轴为两组对边的垂直平分线,对称中心为其对角线的交点
几何语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC
3.直角三角形斜边上的中线等于斜边的一半
D
A
B
C
O
提示:根据矩形的性质,BD=AC
BO= BD= AC
边 角 对角线 对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
4.矩形与平行四边形的性质比较
例1 如图,矩形ABCD的两条对角线相交于点O,
且∠AOB=60°,AB=4 cm.求矩形对角线的长.
A
B
C
D
O
2. 过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是( )
1. 下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
A.对角线相等的四边形
B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形
D.对角线垂直的四边形
D
D
基础训练
3. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为( )
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等于 ( )
A.30° B.45° C.60° D.120°
D
A
例2. 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解: ∵ △AOB、 △BOC、 △COD
和△AOD四个三角形的周长和为86cm,
又∵
AC=BD=13cm,
∴ AB+BC+CD+DA
=86-2(AC+BD)
=86-4×13=34(cm).
即矩形ABCD的周长等于34cm.
A D
B C
O
矩形的两条对角线将矩形分成两对全等的等腰三角形,并且分成的四个等腰三角形面积相等。
平行四边形的两条条对角线将平行四边形分为两对全等的三角形且分成的四个三角形面积相等。
归纳总结:
1.如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F.若BE=3,AF=5,则AC的长为( ) A.4 B.4 C.10 D.8
拓展提升
A
2.如图,在矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交边AB,CD于点E,F. (1)求证:四边形DEBF是平行四边形; (2)当DE=DF时,求EF的长.
(1)证明:∵四边形ABCD是矩形, ∴AB∥CD. ∴∠ODF=∠OBE. ∵点O是对角线BD的中点, ∴OD=OB. 又∵∠DOF=∠BOE, ∴△DOF≌△BOE(ASA). ∴DF=BE. 又∵DF∥BE, ∴四边形DEBF是平行四边形.
(2)解:∵DE=DF,四边形DEBF是平行四边形, ∴四边形DEBF是菱形. ∴DE=BE,EF⊥BD,OE=OF. 设AE=x,则DE=BE=8-x. 在Rt△ADE中,根据勾股定理,得AE2+AD2=DE2, 即x2+62=(8-x)2, 解得x=7/4. ∴DE=8-7/4=25/4. 在Rt△ABD中,根据勾股定理,得 BD==10. ∴OD=1/2BD=5. 在Rt△DOE中,根据勾股定理,得 OE=15/4. ∴EF=2OE=15/2.
3.如图,在Rt△ABC中,∠ACB=90°,∠A=30°.点D是AB的中点,点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边△DEF,连接BF. 判断△BCD的形状;
人教版八年级数学
第十八章 平行四边形
18.2.1矩形的性质(第一课时)
课标解读
1.理解矩形的定义,能够把矩形的定义作为性质和判定进行运用。
2.掌握矩形的性质定理,并能灵活运用这些性质定理解决问题。
3.理解并掌握直角三角形斜边上的中线的性质,并能利用这一性质进行有关的计算和证明。
知识梳理
1.矩形的定义:有一个角是直角的平行四边形是矩形,也称为长方形
温馨提示:矩形的定义有两个要素:
①四边形是平行四边形
②有一个角是直角,二者缺一不可。
A
B
C
D
矩形是特殊的平行四边形,因此它具有平行四边形的所有性质,但它也有自己独特的性质。
2.矩形的性质(从边、角、对角线三个方面总结)
(1).边:①两组对边分别平行
② 两组对边分别相等
A
B
C
D
几何语言:∵四边形ABCD是矩形
∴AB//CD,AD//BC
AB=CD,AD=BC
(2)角:矩形的四个角都是直角
A
B
C
D
几何语言:∵四边形ABCD是矩形
∴∠BAD=∠ADC=∠DCB=∠DCB=90°
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,
求证:∠A=∠B=∠C=∠D=90°.
A
B
C
D
证明: ∵四边形ABCD是矩形,
∴ ∠A=90°.
又 矩形ABCD是平行四边形,
∴ ∠A=∠C ∠B = ∠D.
∠A +∠B = 90°.
∴ ∠A=∠B=∠C=∠D=90°,
即矩形的四个角都是直角.
(3)对角线:矩形的对角线互相平分且相等
几何语言:∵四边形ABCD是矩形
∴OA=OC,OB=OD,AC=BD
已知:如图,四边形ABCD是矩形,
求证:AC = BD.
A
B
C
D
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
又∵AB = DC , BC = CB,
∴△ABC≌△DCB.
∴AC = BD, 即矩形的对角线相等.
求证:矩形的对角线相等
(4)对称性:既是轴对称图形,又是中心对称图形,有两条对称轴,其对称轴为两组对边的垂直平分线,对称中心为其对角线的交点
几何语言: ∵在Rt△ABC中, BO是斜边AC上的中线
∴ BO= AC
3.直角三角形斜边上的中线等于斜边的一半
D
A
B
C
O
提示:根据矩形的性质,BD=AC
BO= BD= AC
边 角 对角线 对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
4.矩形与平行四边形的性质比较
例1 如图,矩形ABCD的两条对角线相交于点O,
且∠AOB=60°,AB=4 cm.求矩形对角线的长.
A
B
C
D
O
2. 过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是( )
1. 下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
A.对角线相等的四边形
B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形
D.对角线垂直的四边形
D
D
基础训练
3. 已知矩形的一条对角线与一边的夹角是40°,则两条对角线所夹锐角的度数为( )
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等于 ( )
A.30° B.45° C.60° D.120°
D
A
例2. 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
解: ∵ △AOB、 △BOC、 △COD
和△AOD四个三角形的周长和为86cm,
又∵
AC=BD=13cm,
∴ AB+BC+CD+DA
=86-2(AC+BD)
=86-4×13=34(cm).
即矩形ABCD的周长等于34cm.
A D
B C
O
矩形的两条对角线将矩形分成两对全等的等腰三角形,并且分成的四个等腰三角形面积相等。
平行四边形的两条条对角线将平行四边形分为两对全等的三角形且分成的四个三角形面积相等。
归纳总结:
1.如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F.若BE=3,AF=5,则AC的长为( ) A.4 B.4 C.10 D.8
拓展提升
A
2.如图,在矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交边AB,CD于点E,F. (1)求证:四边形DEBF是平行四边形; (2)当DE=DF时,求EF的长.
(1)证明:∵四边形ABCD是矩形, ∴AB∥CD. ∴∠ODF=∠OBE. ∵点O是对角线BD的中点, ∴OD=OB. 又∵∠DOF=∠BOE, ∴△DOF≌△BOE(ASA). ∴DF=BE. 又∵DF∥BE, ∴四边形DEBF是平行四边形.
(2)解:∵DE=DF,四边形DEBF是平行四边形, ∴四边形DEBF是菱形. ∴DE=BE,EF⊥BD,OE=OF. 设AE=x,则DE=BE=8-x. 在Rt△ADE中,根据勾股定理,得AE2+AD2=DE2, 即x2+62=(8-x)2, 解得x=7/4. ∴DE=8-7/4=25/4. 在Rt△ABD中,根据勾股定理,得 BD==10. ∴OD=1/2BD=5. 在Rt△DOE中,根据勾股定理,得 OE=15/4. ∴EF=2OE=15/2.
3.如图,在Rt△ABC中,∠ACB=90°,∠A=30°.点D是AB的中点,点E为边AC上一点,连接CD,DE,以DE为边在DE的左侧作等边△DEF,连接BF. 判断△BCD的形状;
