北师大版八年级下册数学 5.3分式的加减法(2)—分式的通分 课件 (共18张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 5.3分式的加减法(2)—分式的通分 课件 (共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 657.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-28 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
5.3分式的加减法(2)-----分式的通分
《数学》(北师大.八年级 下册)
第五章分式与分式方程
1.分式的基本性质:
一个分式的分子与分母___________(或除以)一个
的整式,分式的值不变.
用字母表示为:
,
(C≠0)
2.分式的符号法则:
(一)复习旧知
不等于0
同乘
偶数个为“正”;奇数个为“负”;
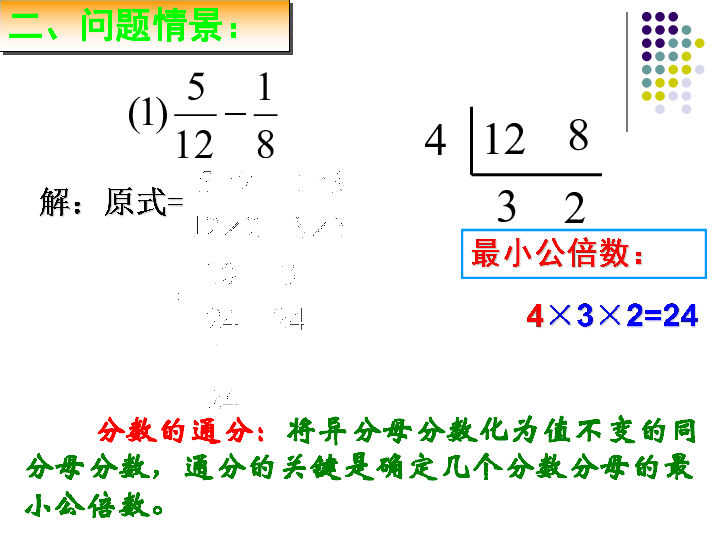
最小公倍数:
4×3×2=24
二、问题情景:
解:原式=
分数的通分:将异分母分数化为值不变的同分母分数,通分的关键是确定几个分数分母的最小公倍数。
1.你运用什么数学原理进行分式变形?
探究
1.利用分式的基本性质填空
三、新课:
2.分式变形后,各分母有什么变化?
3.这样的分式变形叫什么?
分式的通分
与分数的通分类似,也可以利用分式的基本性质,将分子和分母同乘适当的整式,不改变分式的值,把异分母分式化成同分母的分式,这样的分式变形叫做分式的通分。
分析:分式通分的关键是确定几个分式的公分母,通常取各分母所有因式的最高次幂的积作为公分母,也叫最简公分母.
问题:如何找最简公分母?
最小公倍数
最高次幂
所有字母
2
2
1.分母是单项式时,应取系数的 ,取所有字母的最 次幂的积作最简公分母;
最小公倍数
高
分母为多项式时,取不同的因式
一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母。
最简公分母
2.分母是多项式时,先 ,取系数的 ,所有因式的最 次幂的积作最简公分母。
分解因式
最小公倍数
高
3、练习:找最简公分母
解:最简公分母是:
解:最简公分母是:
解:最简公分母是:
解:最简公分母是:
6
解:
最简公分母是
四、例题:
通分:
解:
最简公分母是
最简公分母是
解:
(3)
∵ x?-y?=________________,
x?+xy=_____________,
∴ 与 的最简公分母为____________,
∴
x?+xy
1
x?-y?
1
x?+xy
1
x?-y?
1
(x+y)(x-y)
x(x+y)
x(x+y)(x-y)
分母是多项式,先把分母分解因式
归纳
异分母分式通分的步骤是:
1、求出所有分式分母的最简公分母
2、将所有分式的分母变为最简公分母,同时各分式按照分母所扩大的倍数,相应扩大各自的分子。
3. 三个分式 的最简公分母 是 ;
1.三个分式
的最简公分母是( )
B.
C.
D.
2.分式
的最简公分母是_______.
A.
五、补充练习:
C
1.通分:
2.(补充)通分:
练习:
1、把各分式化成相同分母的分式叫做
分式的通分.
2、最简公分母:
(1)系数:
最小公倍数
(2)字母:
所有字母(或因式)取最高次幂
小结
再见!
5.3分式的加减法(2)-----分式的通分
《数学》(北师大.八年级 下册)
第五章分式与分式方程
1.分式的基本性质:
一个分式的分子与分母___________(或除以)一个
的整式,分式的值不变.
用字母表示为:
,
(C≠0)
2.分式的符号法则:
(一)复习旧知
不等于0
同乘
偶数个为“正”;奇数个为“负”;
最小公倍数:
4×3×2=24
二、问题情景:
解:原式=
分数的通分:将异分母分数化为值不变的同分母分数,通分的关键是确定几个分数分母的最小公倍数。
1.你运用什么数学原理进行分式变形?
探究
1.利用分式的基本性质填空
三、新课:
2.分式变形后,各分母有什么变化?
3.这样的分式变形叫什么?
分式的通分
与分数的通分类似,也可以利用分式的基本性质,将分子和分母同乘适当的整式,不改变分式的值,把异分母分式化成同分母的分式,这样的分式变形叫做分式的通分。
分析:分式通分的关键是确定几个分式的公分母,通常取各分母所有因式的最高次幂的积作为公分母,也叫最简公分母.
问题:如何找最简公分母?
最小公倍数
最高次幂
所有字母
2
2
1.分母是单项式时,应取系数的 ,取所有字母的最 次幂的积作最简公分母;
最小公倍数
高
分母为多项式时,取不同的因式
一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母。
最简公分母
2.分母是多项式时,先 ,取系数的 ,所有因式的最 次幂的积作最简公分母。
分解因式
最小公倍数
高
3、练习:找最简公分母
解:最简公分母是:
解:最简公分母是:
解:最简公分母是:
解:最简公分母是:
6
解:
最简公分母是
四、例题:
通分:
解:
最简公分母是
最简公分母是
解:
(3)
∵ x?-y?=________________,
x?+xy=_____________,
∴ 与 的最简公分母为____________,
∴
x?+xy
1
x?-y?
1
x?+xy
1
x?-y?
1
(x+y)(x-y)
x(x+y)
x(x+y)(x-y)
分母是多项式,先把分母分解因式
归纳
异分母分式通分的步骤是:
1、求出所有分式分母的最简公分母
2、将所有分式的分母变为最简公分母,同时各分式按照分母所扩大的倍数,相应扩大各自的分子。
3. 三个分式 的最简公分母 是 ;
1.三个分式
的最简公分母是( )
B.
C.
D.
2.分式
的最简公分母是_______.
A.
五、补充练习:
C
1.通分:
2.(补充)通分:
练习:
1、把各分式化成相同分母的分式叫做
分式的通分.
2、最简公分母:
(1)系数:
最小公倍数
(2)字母:
所有字母(或因式)取最高次幂
小结
再见!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
