鲁教版六年级数学下册第八章 数据的收集与整理综合测评(含答案)
文档属性
| 名称 | 鲁教版六年级数学下册第八章 数据的收集与整理综合测评(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 211.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-28 11:58:06 | ||
图片预览


文档简介
第八章 数据的收集与整理综合测评
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.为了解广州市2018年中考数学各分数段成绩分布情况,从中抽取400名考生的中考数学成绩进行统计
分析,在这个问题中,样本是指( )
A.400 B.400名考生的中考数学成绩
C.被抽取的400名考生的中考数学成绩 D.广州市2018年中考数学成绩
2.下列调查中,最适合采用全面调查方式的是( )
A.对国庆期间某地游客满意度的调查 B.对某班学生数学作业量的调查
C.对全国中学生手机使用时间情况的调查 D.环保部门对嘉陵江水质情况的调查
3.要调查惠州市中学生了解禁毒知识的情况,下列抽样调查最适合的是( )
A.在某中学随机抽取200名女生 B.在惠州市中学生中随机抽取200名学生
C.在某中学随机抽取200名学生 D.在惠州市中学生中随机抽取200名男生
4.某青年足球队12名队员的年龄情况如下表所示:
?年龄(岁) 18? 19? 20? ?21 ?22
人数(划记) ? ? ? ? ?
人数最多一组的年龄是( )
A.19岁 B.20岁 C.21岁 D.22岁
5.某单位有A,B,C,D,E,F六位司机,12月份的耗油费用如下表:
司机 A B C D E F
耗油费用/元 110 100 105 145 95 98
根据表中的数据作出统计图,以便更清楚地了解每个人的耗油费用,那么应采用( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.三种都可以
6.一个容量为80的样本,其最大值是133,最小值是51,若确定组距为10,则可以分成的组数为( )
A.10组 B.9组 C.8组 D.7组
7.七年级(8)班的同学根据兴趣分成五个小组,各小组人数如图1所示.若用扇形统计图表示各小组的人数,则在扇形图中第5小组对应的圆心角度数是( )
A.45° B.60° C.72° D .120°
图1 图2 图3 图4
8.小明同学根据全班各种血型的人数绘制了图2所示的扇形统计图,若全班A型血有20人,则该班AB型血的人数为( )
A.2人 B.5人 C.8人 D.10人
9.2018年1~4月我国新能源乘用车的月销量情况如图3所示,下列说法中错误的是( )
A.1月份销量为2.2万辆 B.2~3月的月销量增长最快
C.4月份销量比3月份增加了1万辆 D.1~4月新能源乘用车销量逐月增加
10.图4是七年级(1)班同学的一次体检中每分钟心跳次数的频数分布直方图(次数均为整数),从左到右依次为第一、二、三、四小组.已知该班只有5位同学的心跳每分钟75次,有下列说法:①数据75落在第2小组;②第4小组的人数占总人数的10%;③心跳为每分钟75次的人数占该班人数的.
其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(本大题共6小题,每小题3分,共18分)
11.为了解10 000只灯泡的使用寿命,从中抽取50只进行试验,则该次调查的样本容量是 .
12. 某区有15 所中学,其中九年级学生共有 000 名.为了解该区九年级学生的体重情况,请你运用所学的统
计知识,将解决上述问题要经历的几个重要步骤进行排序.①收集数据;②设计调查问卷;③用样本估计总体;④整理数据;⑤分析数据.正确的排序为 ?(填序号).
13.已知样本25,21,25,21,23,25,27,29,25,28,30,29,26,24,25,27,26,22,24,25,26,28若组距为2,那么在24.5~26.5这一组的频数是 .
14.某校为开展“每天运动一小时”活动,对100名学生各自最喜爱的一项体育活动进行调查,制成了图5所示的扇形统计图,则在被调查的学生中,最喜爱打羽毛球的学生人数是 人.
图5 图6
15.某地初中升学考试各学科及满分值情况如下表:
若把该市初中升学考试各学科满分值比例绘成扇形统计图,则数学所在的扇形的圆心角约是_________度.(保留一位小数)
16.七年级(1)班在一次数学抽测中某道选择题的答题情况的统计图如图6所示,根据统计图可得选C的有
人.
三、解答题(本大题共6小题,共52分)
17.(6分) 要调查下列问题,你觉得应采用全面调查还是抽样调查?简要说说理由.
(1)某棉布厂了解一批棉花的纤维长度的情况;
(2)一个水库养了某种鱼10万条,调查这个水库中该种鱼的平均质量.
18.(8分)某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如下不完整的统计表:
分数段 频数 所占百分比
60≤m<70 38 38%
70≤m<80 a 32%
80≤m<90 b c
90≤m≤100 10 10%
合 计 100%
请根据以上信息,解决下列问题:
(1)频数分布表中 c= ;
(2)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
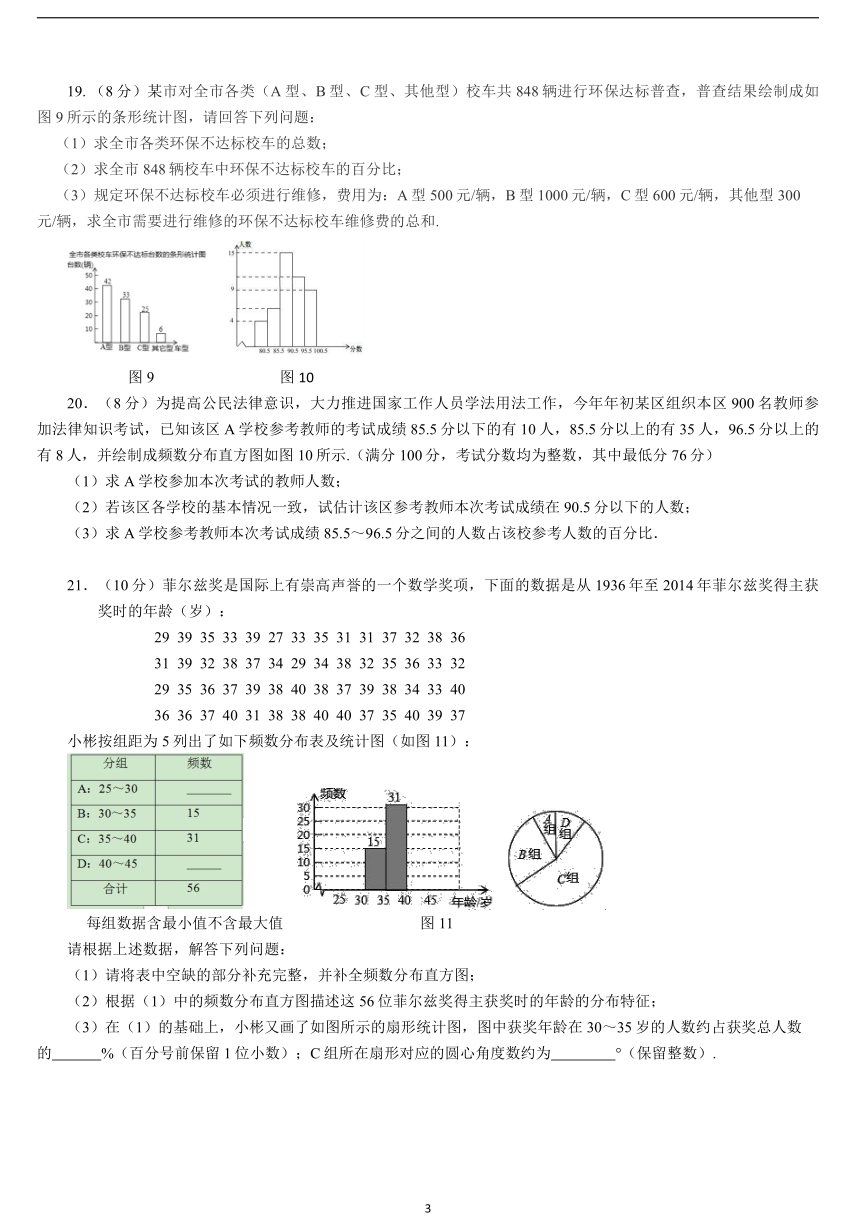
19. (8分)某市对全市各类(A型、B型、C型、其他型)校车共848辆进行环保达标普查,普查结果绘制成如图9所示的条形统计图,请回答下列问题:
(1)求全市各类环保不达标校车的总数;
(2)求全市848辆校车中环保不达标校车的百分比;
(3)规定环保不达标校车必须进行维修,费用为:A型500元/辆,B型1000元/辆,C型600元/辆,其他型300
元/辆,求全市需要进行维修的环保不达标校车维修费的总和.
图9 图10
20.(8分)为提高公民法律意识,大力推进国家工作人员学法用法工作,今年年初某区组织本区900名教师参加法律知识考试,已知该区A学校参考教师的考试成绩85.5分以下的有10人,85.5分以上的有35人,96.5分以上的有8人,并绘制成频数分布直方图如图10所示.(满分100分,考试分数均为整数,其中最低分76分)
(1)求A学校参加本次考试的教师人数;
(2)若该区各学校的基本情况一致,试估计该区参考教师本次考试成绩在90.5分以下的人数;
(3)求A学校参考教师本次考试成绩85.5~96.5分之间的人数占该校参考人数的百分比.
21.(10分)菲尔兹奖是国际上有崇高声誉的一个数学奖项,下面的数据是从1936年至2014年菲尔兹奖得主获奖时的年龄(岁):
29 39 35 33 39 27 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 32
29 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
小彬按组距为5列出了如下频数分布表及统计图(如图11):
每组数据含最小值不含最大值 图11
请根据上述数据,解答下列问题:
(1)请将表中空缺的部分补充完整,并补全频数分布直方图;
(2)根据(1)中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征;
(3)在(1)的基础上,小彬又画了如图所示的扇形统计图,图中获奖年龄在30~35岁的人数约占获奖总人数
的 %(百分号前保留1位小数);C组所在扇形对应的圆心角度数约为 °(保留整数).
22.(12分)某软件科技公司20人负责研发与维护“游戏、网购、视频和送餐”共4款软件.投入市场后,游戏软件的利润占这4款软件总利润的40%.图12是这4款软件研发与维护人数的扇形统计图和利润的条形统计图.
根据以上信息,网答下列问题
(1)直接写出图中a,m的值;
(2)分别求网购与视频软件的人均利润;
(3)在总人数和各款软件人均利润都保持不变的情况下,能否只调整网购与视频软件的研发与维护人数,使总利
润增加60万元?如果能,写出调整方案;如果不能,请说明理由.
第八章 数据的收集与整理综合测评参考答案
一、1. C 2. B 3.B 4. A 5. A 6. B 7.B 8.B 9.D 10.D
二、11. 50 12. ②①④⑤③ 13. 9
14. 35 15. 63.5 16. 28
三、17.解:(1)适合采用抽样调查,因为调查具有破坏性;
(2)适合采用抽样调查,因为调查的容量太大且全面调查难度较大.
18. 解:(1)20%
(2)全市获得一等奖征文的篇数约为:1000×(20%+10%)=300(篇).
19.解:(1)全市各类环保不达标校车的总数为:42+33+25+6=106(辆);
(2)全市848辆校车中环保不达标校车的百分比为:×100%=12.5%;
(3)全市需要进行维修的环保不达标校车维修费的总和为:500×42+1000×33+600×25+300×6=70 800(元).
20. 解: (1)由已知,知85.5分以下有
10人,85.5分以上有35人,所以A学校参加本次考试的教师人数为45人;
(2)由已知85.5分以下有10人,由频数分布直方图知85.5~90.5之间有15人,故该区参考教师本次考试成绩在90.5分以下的人数为:×900=500(人);
(3)由已知96.5分以上有8人,由频数分布直方图知95.5~100.5之间有9人,所以96分的有1人,90.5~95.5之间有:35-15-9=11(人).
所以A学校参考教师本次考试成绩在85.5~96.5分之间的人数占该校参考人数的百分比为:×100%=60%.
21. 解: (1)频数分布表中从上到下依次填4,6.补全频数分布直方图如下:
(2)由频数分布直方图知,这56位菲尔兹奖得主获奖时的年龄主要分布在35~40岁;
(3)26.8 199 提示:获奖年龄在30~35岁的人数约占获奖总人数百分比为:×100%≈26.8%;C组所在扇
形对应的圆心角度数约为:×360°≈199°.
22. 解: (1)a=100-(10+40+30)=20.
因为软件总利润为1200÷40%=3000,所以m=3000-(1200+560+280)=960;
(2)网购软件的人均利润为=
160(万元/人),视频软件的人均利润=140(万元/人);
(3)能.调整方案如下:
设调整后网购的人数为x,则视频的人数为(10-x)人.
根据题意,得1200+280+160x+140(10-x)=3000+60,解得x=9.
即安排9人负责网购、安排1人负责视频可以使总利润增加60万元.
(
2
)
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.为了解广州市2018年中考数学各分数段成绩分布情况,从中抽取400名考生的中考数学成绩进行统计
分析,在这个问题中,样本是指( )
A.400 B.400名考生的中考数学成绩
C.被抽取的400名考生的中考数学成绩 D.广州市2018年中考数学成绩
2.下列调查中,最适合采用全面调查方式的是( )
A.对国庆期间某地游客满意度的调查 B.对某班学生数学作业量的调查
C.对全国中学生手机使用时间情况的调查 D.环保部门对嘉陵江水质情况的调查
3.要调查惠州市中学生了解禁毒知识的情况,下列抽样调查最适合的是( )
A.在某中学随机抽取200名女生 B.在惠州市中学生中随机抽取200名学生
C.在某中学随机抽取200名学生 D.在惠州市中学生中随机抽取200名男生
4.某青年足球队12名队员的年龄情况如下表所示:
?年龄(岁) 18? 19? 20? ?21 ?22
人数(划记) ? ? ? ? ?
人数最多一组的年龄是( )
A.19岁 B.20岁 C.21岁 D.22岁
5.某单位有A,B,C,D,E,F六位司机,12月份的耗油费用如下表:
司机 A B C D E F
耗油费用/元 110 100 105 145 95 98
根据表中的数据作出统计图,以便更清楚地了解每个人的耗油费用,那么应采用( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.三种都可以
6.一个容量为80的样本,其最大值是133,最小值是51,若确定组距为10,则可以分成的组数为( )
A.10组 B.9组 C.8组 D.7组
7.七年级(8)班的同学根据兴趣分成五个小组,各小组人数如图1所示.若用扇形统计图表示各小组的人数,则在扇形图中第5小组对应的圆心角度数是( )
A.45° B.60° C.72° D .120°
图1 图2 图3 图4
8.小明同学根据全班各种血型的人数绘制了图2所示的扇形统计图,若全班A型血有20人,则该班AB型血的人数为( )
A.2人 B.5人 C.8人 D.10人
9.2018年1~4月我国新能源乘用车的月销量情况如图3所示,下列说法中错误的是( )
A.1月份销量为2.2万辆 B.2~3月的月销量增长最快
C.4月份销量比3月份增加了1万辆 D.1~4月新能源乘用车销量逐月增加
10.图4是七年级(1)班同学的一次体检中每分钟心跳次数的频数分布直方图(次数均为整数),从左到右依次为第一、二、三、四小组.已知该班只有5位同学的心跳每分钟75次,有下列说法:①数据75落在第2小组;②第4小组的人数占总人数的10%;③心跳为每分钟75次的人数占该班人数的.
其中正确的说法有( )
A.0个 B.1个 C.2个 D.3个
二、填空题(本大题共6小题,每小题3分,共18分)
11.为了解10 000只灯泡的使用寿命,从中抽取50只进行试验,则该次调查的样本容量是 .
12. 某区有15 所中学,其中九年级学生共有 000 名.为了解该区九年级学生的体重情况,请你运用所学的统
计知识,将解决上述问题要经历的几个重要步骤进行排序.①收集数据;②设计调查问卷;③用样本估计总体;④整理数据;⑤分析数据.正确的排序为 ?(填序号).
13.已知样本25,21,25,21,23,25,27,29,25,28,30,29,26,24,25,27,26,22,24,25,26,28若组距为2,那么在24.5~26.5这一组的频数是 .
14.某校为开展“每天运动一小时”活动,对100名学生各自最喜爱的一项体育活动进行调查,制成了图5所示的扇形统计图,则在被调查的学生中,最喜爱打羽毛球的学生人数是 人.
图5 图6
15.某地初中升学考试各学科及满分值情况如下表:
若把该市初中升学考试各学科满分值比例绘成扇形统计图,则数学所在的扇形的圆心角约是_________度.(保留一位小数)
16.七年级(1)班在一次数学抽测中某道选择题的答题情况的统计图如图6所示,根据统计图可得选C的有
人.
三、解答题(本大题共6小题,共52分)
17.(6分) 要调查下列问题,你觉得应采用全面调查还是抽样调查?简要说说理由.
(1)某棉布厂了解一批棉花的纤维长度的情况;
(2)一个水库养了某种鱼10万条,调查这个水库中该种鱼的平均质量.
18.(8分)某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如下不完整的统计表:
分数段 频数 所占百分比
60≤m<70 38 38%
70≤m<80 a 32%
80≤m<90 b c
90≤m≤100 10 10%
合 计 100%
请根据以上信息,解决下列问题:
(1)频数分布表中 c= ;
(2)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
19. (8分)某市对全市各类(A型、B型、C型、其他型)校车共848辆进行环保达标普查,普查结果绘制成如图9所示的条形统计图,请回答下列问题:
(1)求全市各类环保不达标校车的总数;
(2)求全市848辆校车中环保不达标校车的百分比;
(3)规定环保不达标校车必须进行维修,费用为:A型500元/辆,B型1000元/辆,C型600元/辆,其他型300
元/辆,求全市需要进行维修的环保不达标校车维修费的总和.
图9 图10
20.(8分)为提高公民法律意识,大力推进国家工作人员学法用法工作,今年年初某区组织本区900名教师参加法律知识考试,已知该区A学校参考教师的考试成绩85.5分以下的有10人,85.5分以上的有35人,96.5分以上的有8人,并绘制成频数分布直方图如图10所示.(满分100分,考试分数均为整数,其中最低分76分)
(1)求A学校参加本次考试的教师人数;
(2)若该区各学校的基本情况一致,试估计该区参考教师本次考试成绩在90.5分以下的人数;
(3)求A学校参考教师本次考试成绩85.5~96.5分之间的人数占该校参考人数的百分比.
21.(10分)菲尔兹奖是国际上有崇高声誉的一个数学奖项,下面的数据是从1936年至2014年菲尔兹奖得主获奖时的年龄(岁):
29 39 35 33 39 27 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 32
29 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
小彬按组距为5列出了如下频数分布表及统计图(如图11):
每组数据含最小值不含最大值 图11
请根据上述数据,解答下列问题:
(1)请将表中空缺的部分补充完整,并补全频数分布直方图;
(2)根据(1)中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征;
(3)在(1)的基础上,小彬又画了如图所示的扇形统计图,图中获奖年龄在30~35岁的人数约占获奖总人数
的 %(百分号前保留1位小数);C组所在扇形对应的圆心角度数约为 °(保留整数).
22.(12分)某软件科技公司20人负责研发与维护“游戏、网购、视频和送餐”共4款软件.投入市场后,游戏软件的利润占这4款软件总利润的40%.图12是这4款软件研发与维护人数的扇形统计图和利润的条形统计图.
根据以上信息,网答下列问题
(1)直接写出图中a,m的值;
(2)分别求网购与视频软件的人均利润;
(3)在总人数和各款软件人均利润都保持不变的情况下,能否只调整网购与视频软件的研发与维护人数,使总利
润增加60万元?如果能,写出调整方案;如果不能,请说明理由.
第八章 数据的收集与整理综合测评参考答案
一、1. C 2. B 3.B 4. A 5. A 6. B 7.B 8.B 9.D 10.D
二、11. 50 12. ②①④⑤③ 13. 9
14. 35 15. 63.5 16. 28
三、17.解:(1)适合采用抽样调查,因为调查具有破坏性;
(2)适合采用抽样调查,因为调查的容量太大且全面调查难度较大.
18. 解:(1)20%
(2)全市获得一等奖征文的篇数约为:1000×(20%+10%)=300(篇).
19.解:(1)全市各类环保不达标校车的总数为:42+33+25+6=106(辆);
(2)全市848辆校车中环保不达标校车的百分比为:×100%=12.5%;
(3)全市需要进行维修的环保不达标校车维修费的总和为:500×42+1000×33+600×25+300×6=70 800(元).
20. 解: (1)由已知,知85.5分以下有
10人,85.5分以上有35人,所以A学校参加本次考试的教师人数为45人;
(2)由已知85.5分以下有10人,由频数分布直方图知85.5~90.5之间有15人,故该区参考教师本次考试成绩在90.5分以下的人数为:×900=500(人);
(3)由已知96.5分以上有8人,由频数分布直方图知95.5~100.5之间有9人,所以96分的有1人,90.5~95.5之间有:35-15-9=11(人).
所以A学校参考教师本次考试成绩在85.5~96.5分之间的人数占该校参考人数的百分比为:×100%=60%.
21. 解: (1)频数分布表中从上到下依次填4,6.补全频数分布直方图如下:
(2)由频数分布直方图知,这56位菲尔兹奖得主获奖时的年龄主要分布在35~40岁;
(3)26.8 199 提示:获奖年龄在30~35岁的人数约占获奖总人数百分比为:×100%≈26.8%;C组所在扇
形对应的圆心角度数约为:×360°≈199°.
22. 解: (1)a=100-(10+40+30)=20.
因为软件总利润为1200÷40%=3000,所以m=3000-(1200+560+280)=960;
(2)网购软件的人均利润为=
160(万元/人),视频软件的人均利润=140(万元/人);
(3)能.调整方案如下:
设调整后网购的人数为x,则视频的人数为(10-x)人.
根据题意,得1200+280+160x+140(10-x)=3000+60,解得x=9.
即安排9人负责网购、安排1人负责视频可以使总利润增加60万元.
(
2
)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
