人教版八年级下册18.2.3 正方形课件(22张PPT)
文档属性
| 名称 | 人教版八年级下册18.2.3 正方形课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-29 00:00:00 | ||
图片预览




文档简介
课件22张PPT。18.2.3 正方形
(复习课)四边形矩形平行四边形菱形说一说1. 理解并掌握正方形的概念、性质及判定;
2. 经历探索正方形有关性质和判别条件的过程,了解正方形与矩形、菱形的关系.学习目标正方形正方形有一个角是
直角
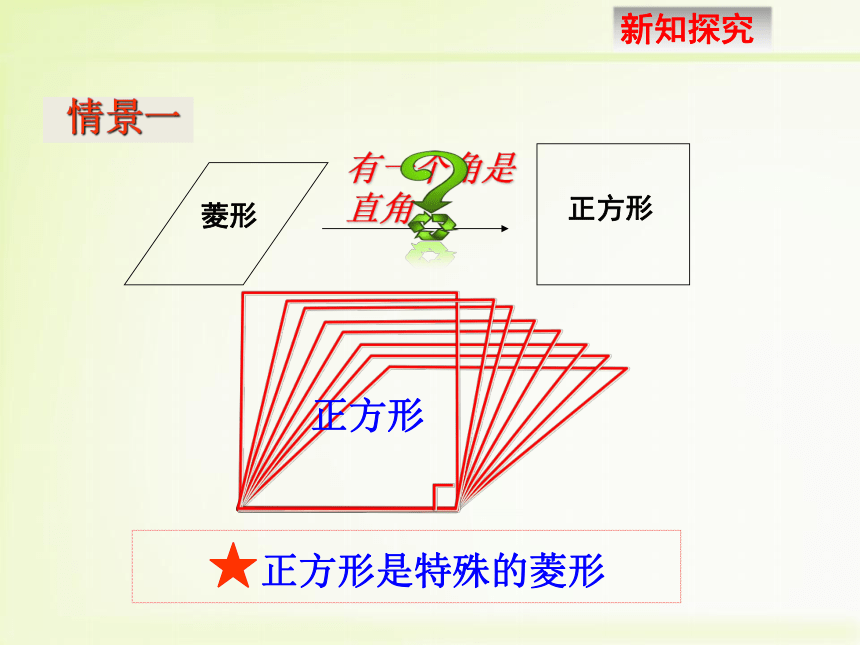
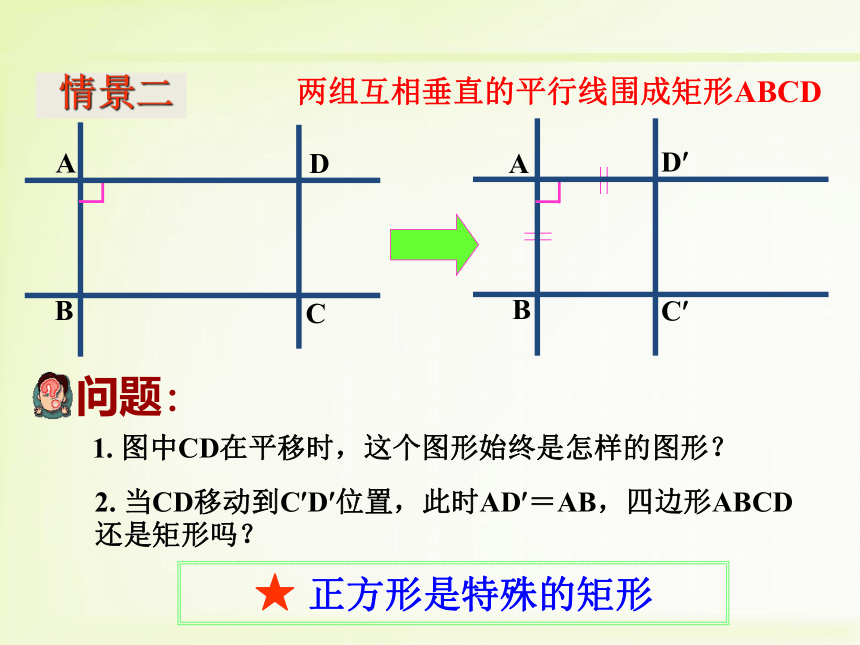
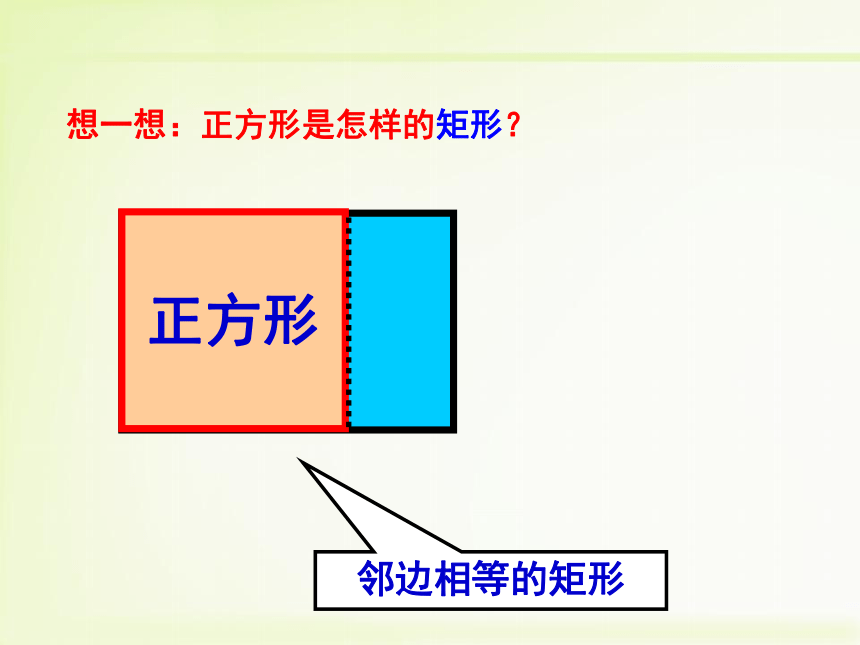
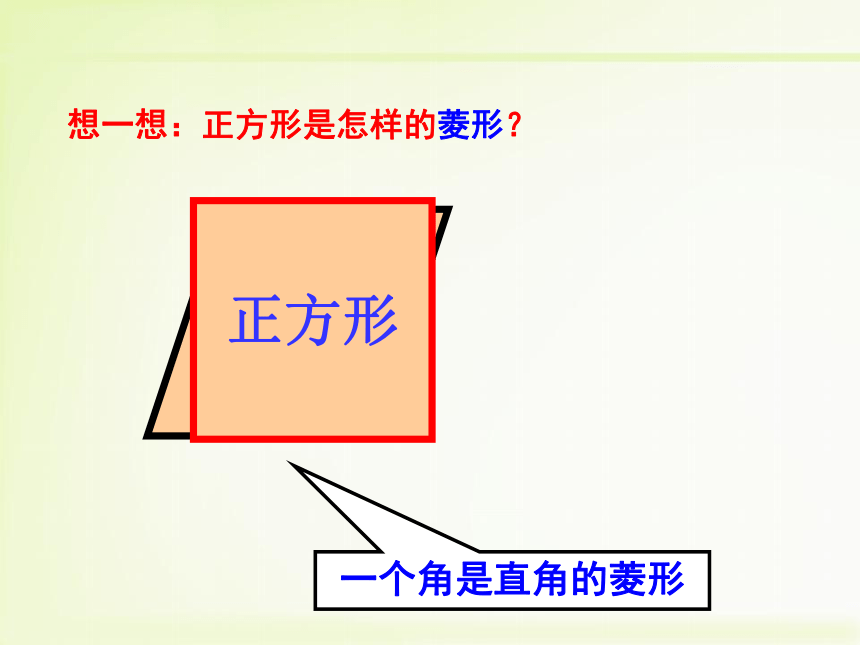
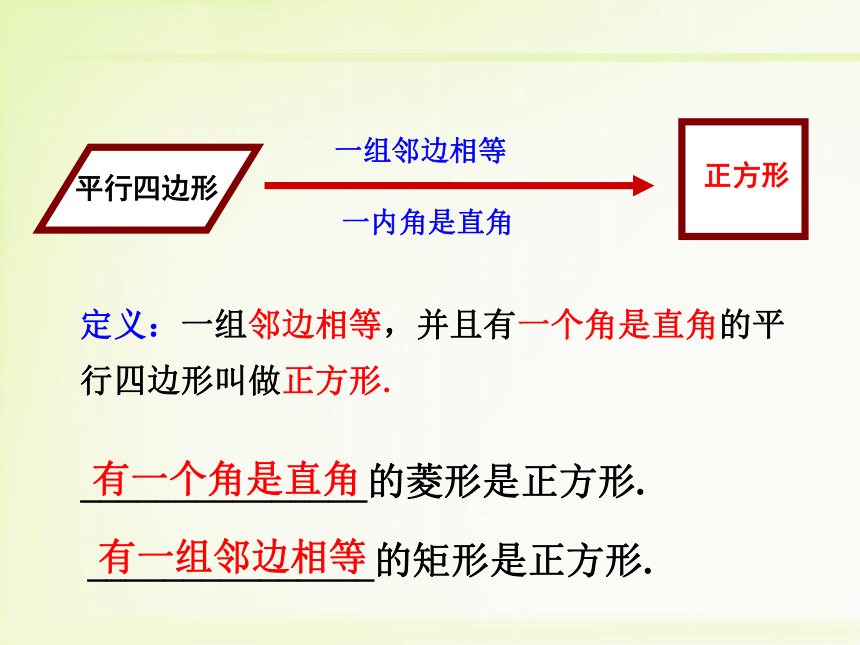
情景一★正方形是特殊的菱形1. 图中CD在平移时,这个图形始终是怎样的图形?2. 当CD移动到C?D?位置,此时AD?=AB,四边形ABCD还是矩形吗?AB★ 正方形是特殊的矩形两组互相垂直的平行线围成矩形ABCD 情景二邻边相等的矩形想一想:正方形是怎样的矩形?矩形正方形一个角是直角的菱形想一想:正方形是怎样的菱形?菱形正方形定义:一组邻边相等,并且有一个角是直角的平行四边形叫做正方形._______________的菱形是正方形. _______________的矩形是正方形.有一个角是直角有一组邻边相等轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,
两组对角相等,
对角线互相平分.(2) 具有矩形的一切性质四个角都是直角,对角线相等.(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角.(A)(B)(C)(D)1、对称性2、性质正方形的判定方法:(可从平行四边形、矩形、菱形为基础)定义法正方形、矩形、菱形以及平行四边形四者之间的关系:有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角 要判定一个三角形是等腰直
角三角形需要什么条件?判定两
个三角形全等的条件又是什么?
图中共有多少个等腰直角三
角形?例1 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.例2:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
(1)试说明:DE=DF
(2)请添加一个条件,使四边形EDFA是正方形.FEDCBA??例3 如图所示,正方形ABCD中,P为BD上一点,PM⊥BC于M, PN⊥DC于N. 试说明:AP=MN证明:连接PC∵PM⊥BC , PN⊥DC 四边形ABCD是正方形∴∠NCM=90°∴四边形PMCN是矩形∴PC=MN又∵四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=MN跟踪练习√×√1.下列说法是否正确,并说明理由.
①对角线相等的菱形是正方形;( )
②对角线互相垂直的矩形是正方形;( )
③对角线垂直且相等的四边形是正方形;( )
④四条边都相等的四边形是正方形;( )
⑤四个角相等的四边形是正方形.( )××对角线________ ,______,_______的四边形是正方形互相垂直相等互相平分__2.如图,已知点A‘、B’、C‘、D’分别是正方形ABCD 四条边上的点, 并且AA‘ =BB’=CC‘= DD’。
求证:四边形A‘B’C‘D’是正方形。跟踪练习证明:在正方形ABCD中, AB=BC=CD=AD,
∵ AA‘ = DD’
∴ AB -AA‘=AD- DD’
∴ A‘B =AD’
又∵∠A=∠D=90°
∴△ABB’≌ △ D AA‘(SAS)
∴A‘D’= A‘B’, ∠2=∠3
∵∠1+∠2=90°
∴∠1+∠3=90°
∴∠ D’A‘B’‘=90°
同理 A‘D’ =C‘D’=B’ C‘= A‘B’
∴∠ D’A‘B’=∠ A‘B’ C‘=
∠ B’ C‘D’ = ∠ A‘D’ C‘=90°∴四边形A‘B’C‘D’是正方形1、如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE,交CD于F,求∠AFC的度数.课堂检测F课堂检测F2、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB.求证:四边形CEDF是正方形.∴四边形ABCD是正方形(有一组邻边相等的矩形是正方形 )∴ DE=DFDE⊥AC, DF⊥BC∵ CD平分∠ACB∴ 四边形ABCD为矩形而∠ACB=90°∴ ∠DEC=90°, ∠DFC=90°证明:∵ DE⊥AC,DF⊥AB课堂检测小结通过这节课的学习你有何收获?1.正方形的定义:2. 3.正方形的性质. 4.正方形的判定
(复习课)四边形矩形平行四边形菱形说一说1. 理解并掌握正方形的概念、性质及判定;
2. 经历探索正方形有关性质和判别条件的过程,了解正方形与矩形、菱形的关系.学习目标正方形正方形有一个角是
直角
情景一★正方形是特殊的菱形1. 图中CD在平移时,这个图形始终是怎样的图形?2. 当CD移动到C?D?位置,此时AD?=AB,四边形ABCD还是矩形吗?AB★ 正方形是特殊的矩形两组互相垂直的平行线围成矩形ABCD 情景二邻边相等的矩形想一想:正方形是怎样的矩形?矩形正方形一个角是直角的菱形想一想:正方形是怎样的菱形?菱形正方形定义:一组邻边相等,并且有一个角是直角的平行四边形叫做正方形._______________的菱形是正方形. _______________的矩形是正方形.有一个角是直角有一组邻边相等轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,
两组对角相等,
对角线互相平分.(2) 具有矩形的一切性质四个角都是直角,对角线相等.(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角.(A)(B)(C)(D)1、对称性2、性质正方形的判定方法:(可从平行四边形、矩形、菱形为基础)定义法正方形、矩形、菱形以及平行四边形四者之间的关系:有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角 要判定一个三角形是等腰直
角三角形需要什么条件?判定两
个三角形全等的条件又是什么?
图中共有多少个等腰直角三
角形?例1 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.例2:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
(1)试说明:DE=DF
(2)请添加一个条件,使四边形EDFA是正方形.FEDCBA??例3 如图所示,正方形ABCD中,P为BD上一点,PM⊥BC于M, PN⊥DC于N. 试说明:AP=MN证明:连接PC∵PM⊥BC , PN⊥DC 四边形ABCD是正方形∴∠NCM=90°∴四边形PMCN是矩形∴PC=MN又∵四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=MN跟踪练习√×√1.下列说法是否正确,并说明理由.
①对角线相等的菱形是正方形;( )
②对角线互相垂直的矩形是正方形;( )
③对角线垂直且相等的四边形是正方形;( )
④四条边都相等的四边形是正方形;( )
⑤四个角相等的四边形是正方形.( )××对角线________ ,______,_______的四边形是正方形互相垂直相等互相平分__2.如图,已知点A‘、B’、C‘、D’分别是正方形ABCD 四条边上的点, 并且AA‘ =BB’=CC‘= DD’。
求证:四边形A‘B’C‘D’是正方形。跟踪练习证明:在正方形ABCD中, AB=BC=CD=AD,
∵ AA‘ = DD’
∴ AB -AA‘=AD- DD’
∴ A‘B =AD’
又∵∠A=∠D=90°
∴△ABB’≌ △ D AA‘(SAS)
∴A‘D’= A‘B’, ∠2=∠3
∵∠1+∠2=90°
∴∠1+∠3=90°
∴∠ D’A‘B’‘=90°
同理 A‘D’ =C‘D’=B’ C‘= A‘B’
∴∠ D’A‘B’=∠ A‘B’ C‘=
∠ B’ C‘D’ = ∠ A‘D’ C‘=90°∴四边形A‘B’C‘D’是正方形1、如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE,交CD于F,求∠AFC的度数.课堂检测F课堂检测F2、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB.求证:四边形CEDF是正方形.∴四边形ABCD是正方形(有一组邻边相等的矩形是正方形 )∴ DE=DFDE⊥AC, DF⊥BC∵ CD平分∠ACB∴ 四边形ABCD为矩形而∠ACB=90°∴ ∠DEC=90°, ∠DFC=90°证明:∵ DE⊥AC,DF⊥AB课堂检测小结通过这节课的学习你有何收获?1.正方形的定义:2. 3.正方形的性质. 4.正方形的判定
