人教版八年级下册数学课件:18.2.1 矩形 (27PPT)
文档属性
| 名称 | 人教版八年级下册数学课件:18.2.1 矩形 (27PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-29 07:56:09 | ||
图片预览





文档简介
(共27张PPT)
18.2.1 矩形(1)
18.2 特殊的平行四边形
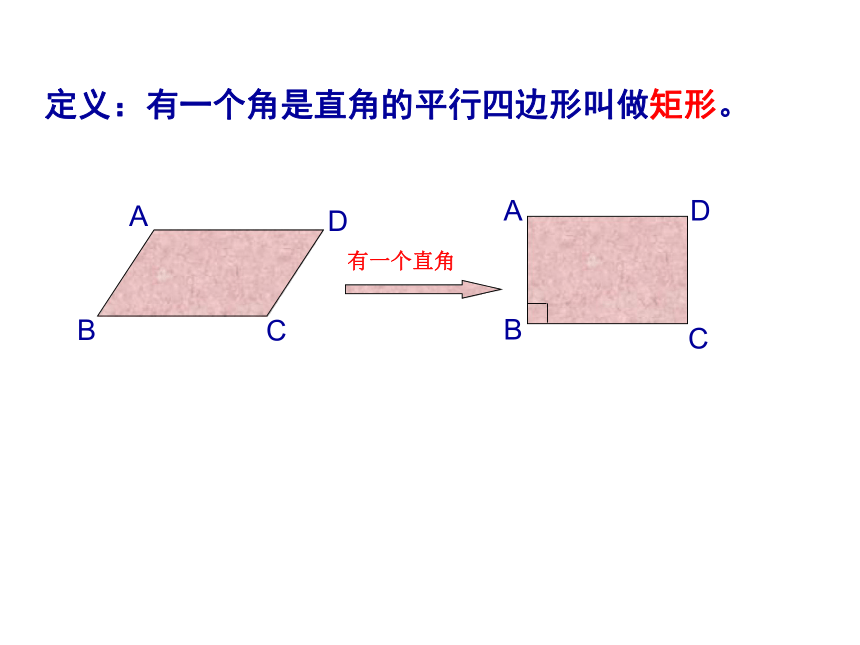
定义:有一个角是直角的平行四边形叫做矩形。
有一个直角
生活中有很多具有矩形形象的物品,
你能举出一些例子吗?
说一说
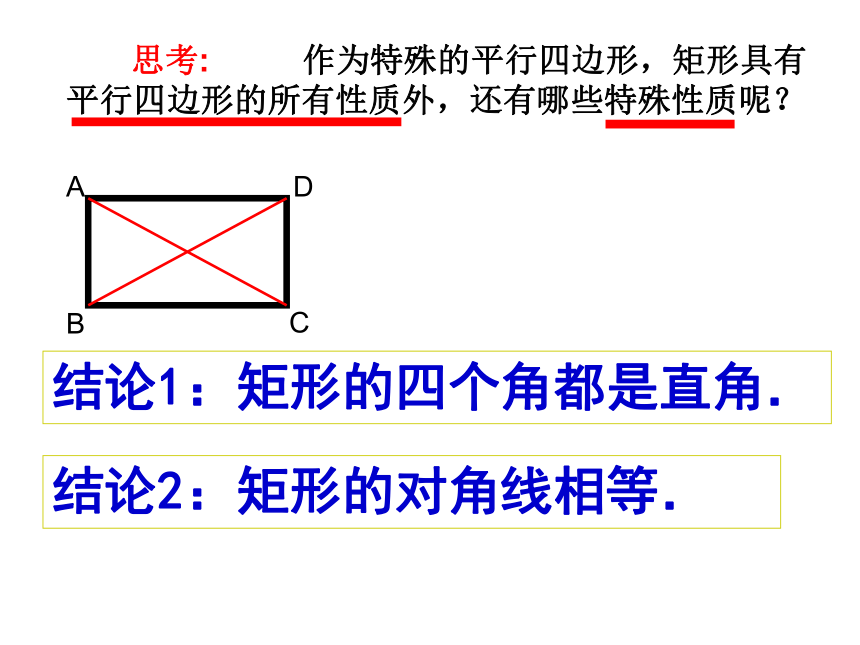
思考: 作为特殊的平行四边形,矩形具有平行四边形的所有性质外,还有哪些特殊性质呢?
结论1:矩形的四个角都是直角.
结论2:矩形的对角线相等.
A
B
C
D
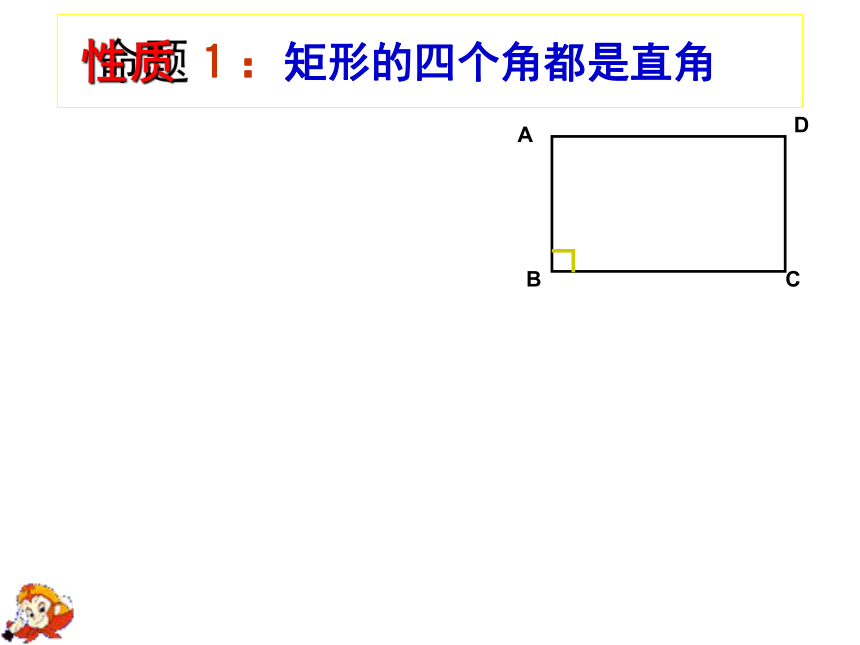
1:矩形的四个角都是直角
D
C
B
A
命题
性质
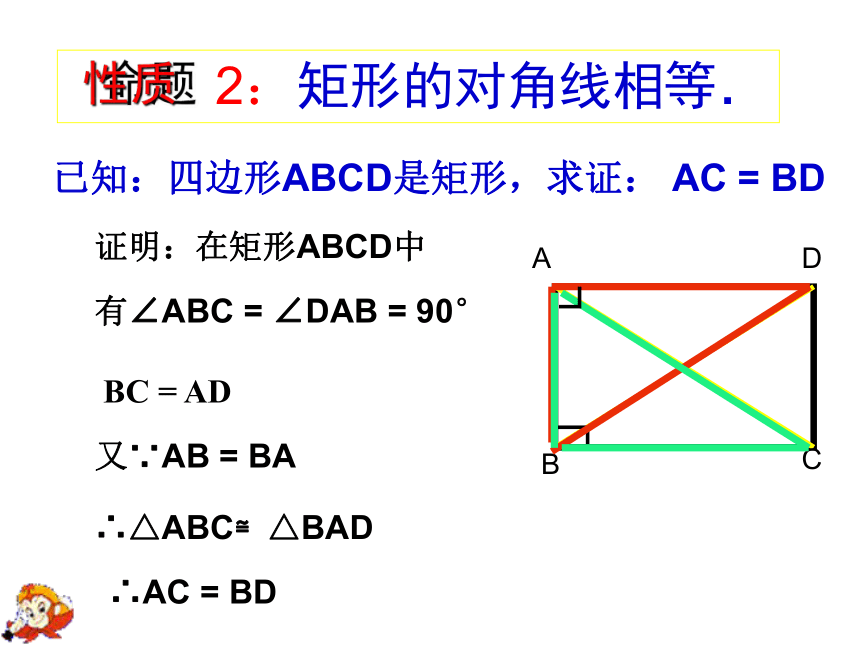
已知:四边形ABCD是矩形,求证: AC = BD
证明:在矩形ABCD中
有∠ABC = ∠DAB = 90°
BC = AD
又∵AB = BA
∴△ABC≌△BAD
∴AC = BD
2:矩形的对角线相等.
命题
性质
矩形的性质:
1、矩形具有平行四边形的所有性质。
2、矩形的四个角都是直角。
3、矩形的对角线相等。
对边平行
且相等
四个角
都是直角
对角线互相
平分且相等
类比总结
公平,因为OA=OC=OB=OD
O
A
B
C
D
O
D
C
B
A
┛
在Rt△ABD中,AO是斜边BD的中线
直角三角形的性质 :
直角三角形斜边上的中线等于斜边的一半。
则有:AO= BD
试试:用文字叙述
直角三角形的性质
在矩形ABCD中
AO=CO=BO=DO= =
思考:在Rt△ABD中,AO和BD是什么关系?
AC
BD
挑战开始
请 选 择
6
2
4
3
5
1
挑战第一关
进入第二关
进入第三关
通关小 结
(快速问答)
1、矩形的定义中有两个条件:
一是:
二是:
有一个角是直角
是一个平行四边形
(请你的同桌回答)
2、矩形具有而一般平行四边形不具有的性质是( )
(A)对角线相等 (B)对边相等
(C)对角相等 (D)对角线互相平分
A
(请你回答)
4、在Rt△ABC中,∠ABC=90°,AC=16,
BO是斜边上的中线,则BO的长为
8
(你请他或她回答)
3、如图,在矩形ABCD中,对角线AC、BD相交于点O,
且AB=6,BC=8,则△ABO的周长为
16
(小组讨论完成后汇报。时间:1分钟)
5、矩形是轴对称图形吗?它的对称轴是什么?
(你请好朋友回答)
是
对边中点连线所在的直线
6、下列说法错误的是( )
(A)矩形的对角线互相平分。
(B)矩形的对角线相等。
(C)有一个角是直角的四边形是矩形。
(D)有一个角是直角的平行四边形叫做矩形。
(请你回答)
C
练习:如图,矩形ABCD的两条对角线相交于点O,
且∠AOB=60°,AB=4 cm.求矩形对角线的长.
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分。
∴OA=OB.
又∠AOB=60°,
∴△OAB是等边三角形。
∴OA=AB=4.
∴AC=BD=2AO=8.
挑战第二关:运用性质 解决问题
练习:如图,在矩形ABCD中,AE平分∠BAD,交
BC于点E,ED=5,EC=3,求矩形的周长及对角线的长。
3
5
4
4
4
7
挑战第三关
谈谈你在这节课中学到了什么?有哪些收获?
课堂小结
直角三角形性质:直角三角形斜边上的中线
等于斜边的一半.
矩形是轴对称图形,有两条对称轴,连接对边中点
的直线是它的两条对称轴.
课堂小结
1、具有平行四边形的所有性质;
2、矩形的四个角都是直角;
3、矩形的对角线相等且互相平分.
矩形:有一个角是直角的平行四边形叫做矩形.
作业:教科书第53页练习第2题;
习题18.2第9题.
课后作业
18.2.1 矩形(1)
18.2 特殊的平行四边形
定义:有一个角是直角的平行四边形叫做矩形。
有一个直角
生活中有很多具有矩形形象的物品,
你能举出一些例子吗?
说一说
思考: 作为特殊的平行四边形,矩形具有平行四边形的所有性质外,还有哪些特殊性质呢?
结论1:矩形的四个角都是直角.
结论2:矩形的对角线相等.
A
B
C
D
1:矩形的四个角都是直角
D
C
B
A
命题
性质
已知:四边形ABCD是矩形,求证: AC = BD
证明:在矩形ABCD中
有∠ABC = ∠DAB = 90°
BC = AD
又∵AB = BA
∴△ABC≌△BAD
∴AC = BD
2:矩形的对角线相等.
命题
性质
矩形的性质:
1、矩形具有平行四边形的所有性质。
2、矩形的四个角都是直角。
3、矩形的对角线相等。
对边平行
且相等
四个角
都是直角
对角线互相
平分且相等
类比总结
公平,因为OA=OC=OB=OD
O
A
B
C
D
O
D
C
B
A
┛
在Rt△ABD中,AO是斜边BD的中线
直角三角形的性质 :
直角三角形斜边上的中线等于斜边的一半。
则有:AO= BD
试试:用文字叙述
直角三角形的性质
在矩形ABCD中
AO=CO=BO=DO= =
思考:在Rt△ABD中,AO和BD是什么关系?
AC
BD
挑战开始
请 选 择
6
2
4
3
5
1
挑战第一关
进入第二关
进入第三关
通关小 结
(快速问答)
1、矩形的定义中有两个条件:
一是:
二是:
有一个角是直角
是一个平行四边形
(请你的同桌回答)
2、矩形具有而一般平行四边形不具有的性质是( )
(A)对角线相等 (B)对边相等
(C)对角相等 (D)对角线互相平分
A
(请你回答)
4、在Rt△ABC中,∠ABC=90°,AC=16,
BO是斜边上的中线,则BO的长为
8
(你请他或她回答)
3、如图,在矩形ABCD中,对角线AC、BD相交于点O,
且AB=6,BC=8,则△ABO的周长为
16
(小组讨论完成后汇报。时间:1分钟)
5、矩形是轴对称图形吗?它的对称轴是什么?
(你请好朋友回答)
是
对边中点连线所在的直线
6、下列说法错误的是( )
(A)矩形的对角线互相平分。
(B)矩形的对角线相等。
(C)有一个角是直角的四边形是矩形。
(D)有一个角是直角的平行四边形叫做矩形。
(请你回答)
C
练习:如图,矩形ABCD的两条对角线相交于点O,
且∠AOB=60°,AB=4 cm.求矩形对角线的长.
解:∵四边形ABCD是矩形,
∴AC与BD相等且互相平分。
∴OA=OB.
又∠AOB=60°,
∴△OAB是等边三角形。
∴OA=AB=4.
∴AC=BD=2AO=8.
挑战第二关:运用性质 解决问题
练习:如图,在矩形ABCD中,AE平分∠BAD,交
BC于点E,ED=5,EC=3,求矩形的周长及对角线的长。
3
5
4
4
4
7
挑战第三关
谈谈你在这节课中学到了什么?有哪些收获?
课堂小结
直角三角形性质:直角三角形斜边上的中线
等于斜边的一半.
矩形是轴对称图形,有两条对称轴,连接对边中点
的直线是它的两条对称轴.
课堂小结
1、具有平行四边形的所有性质;
2、矩形的四个角都是直角;
3、矩形的对角线相等且互相平分.
矩形:有一个角是直角的平行四边形叫做矩形.
作业:教科书第53页练习第2题;
习题18.2第9题.
课后作业
