人教版六年级下册6.2.1 图形的认识与测量(例1—3) 课件(42张ppt)
文档属性
| 名称 | 人教版六年级下册6.2.1 图形的认识与测量(例1—3) 课件(42张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-28 00:00:00 | ||
图片预览







文档简介
(共42张PPT)
第六单元 整理与复习 2.图形与几何
图形的认识与测量(例1—3)
数学人教版 六年级下
1.全面掌握小学阶段所学的平面图形的基本特征,能画出相应的
图形;能正确计算平面图形的周长与面积,并能运用相关知识解
决生活中的实际问题。
2.通过分类、比较、辨析,进一步认识图形的区别与联系,形成
清晰的知识网络。
3.通过整理与复习,借助几何图形的直观性,增强我们的空间观
念和空间想象能力。
学习目标:
平
面
图
形
三角形
按角分
直角三角形
钝角三角形
按边分
不等边三角形
等边三角形
等腰三角形
四边形
平行四边形
四个角
是直角
长方形
四条边
都相等
正方形
梯形
等腰梯形
直角梯形
圆
轴对称图形
图形
锐角三角形
立体图形
长方体
正方体
圆柱
圆锥
想一想,我们都学过哪些平面图形与立体图形?怎样把图形分类。
直线、射线和线段有什么区别和联系?
●
●
●
线段:
射线:
直线:
用直尺把两点连接起来,就得到一条线段;
把线段一端无限延长,可以得到一条射线;
把线段两端无限延长,可以得到一条直线。
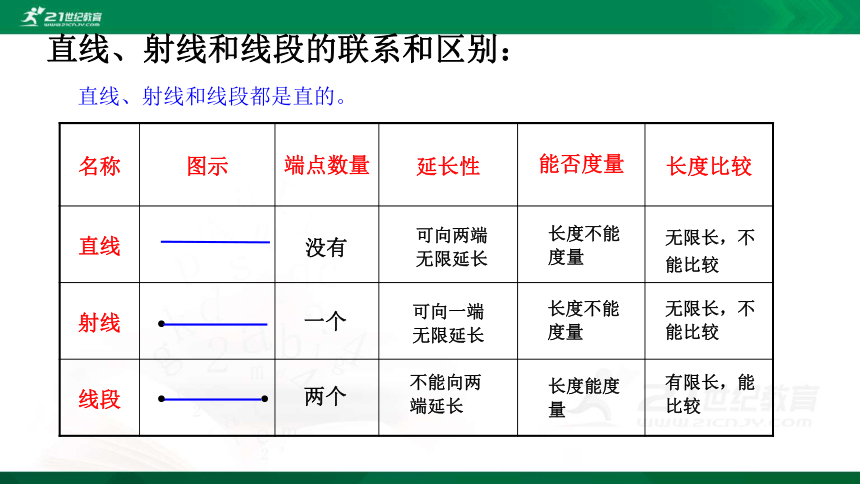
名称 图示 端点数量 延长性 能否度量 长度比较
直线
射线
线段
没有
一个
两个
可向两端
无限延长
可向一端
无限延长
不能向两
端延长
长度不能度量
长度不能度量
长度能度量
无限长,不能比较
无限长,不
能比较
有限长,能比较
直线、射线和线段的联系和区别:
●
●
●
直线、射线和线段都是直的。
经过一点可以画无数条直线。
从一点可以引出无数条射线。
经过两点只可以画一条直线,两点确定一条直线。
重要的“点”:
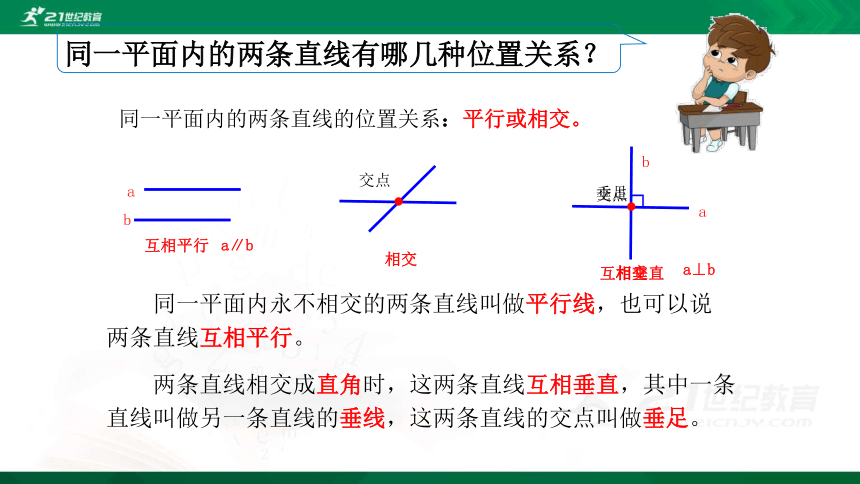
同一平面内的两条直线有哪几种位置关系?
同一平面内的两条直线的位置关系:平行或相交。
同一平面内永不相交的两条直线叫做平行线,也可以说两条直线互相平行。
相交
互相平行
交点
两条直线相交成直角时,这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
相交
垂足
互相垂直
交点
a
b
a∥b
a⊥b
b
a
A
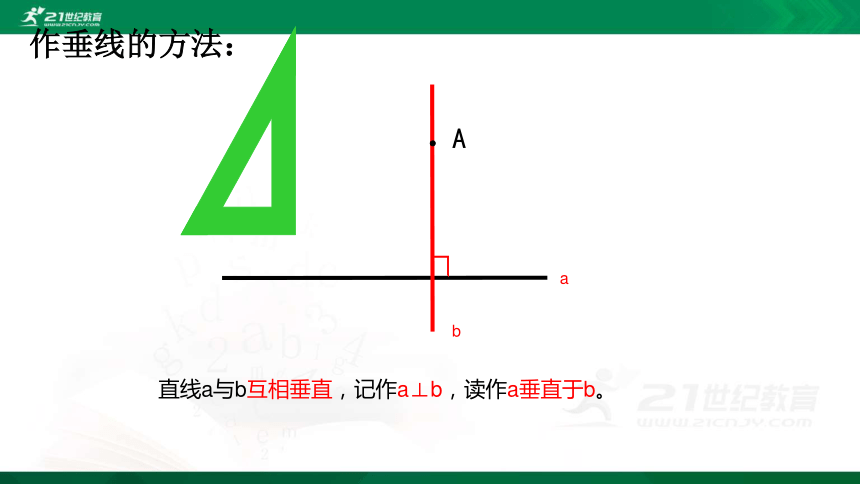
直线a与b互相垂直,记作a⊥b,读作a垂直于b。
a
b
作垂线的方法:
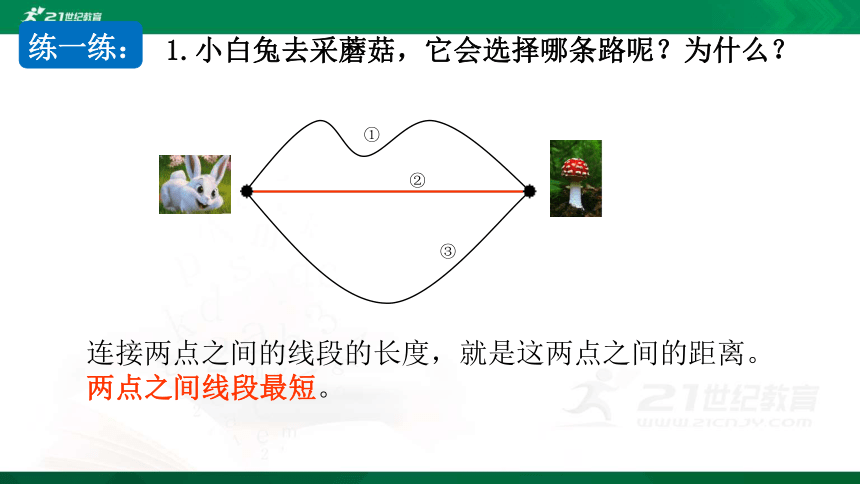
连接两点之间的线段的长度,就是这两点之间的距离。两点之间线段最短。
②
①
③
1.小白兔去采蘑菇,它会选择哪条路呢?为什么?
练一练:
②
①
③
从直线外一点到这条直线所画的垂直线段最短,它的长度叫做点到直线的距离。
两条平行线间的距离处处相等。
2.村民们要修一条水渠与小河相通,要使水渠最短,应该怎样挖?
一组平行线之间的距离,垂直线段最短。
练一练:
水 渠
从一点引出的两条射线所组成的图形叫做角。
顶点
边
边
这个点叫做角的顶点,这两条射线叫做角的边,角通常用符号“∠”来表示。
角的大小要看两边叉开的大小,开口越大,角越大。角的大小与两条边的长短无关。
我们学过哪些角?角的大小和什么有关?
在放大镜下看角,角的大小不变。
1
∠1
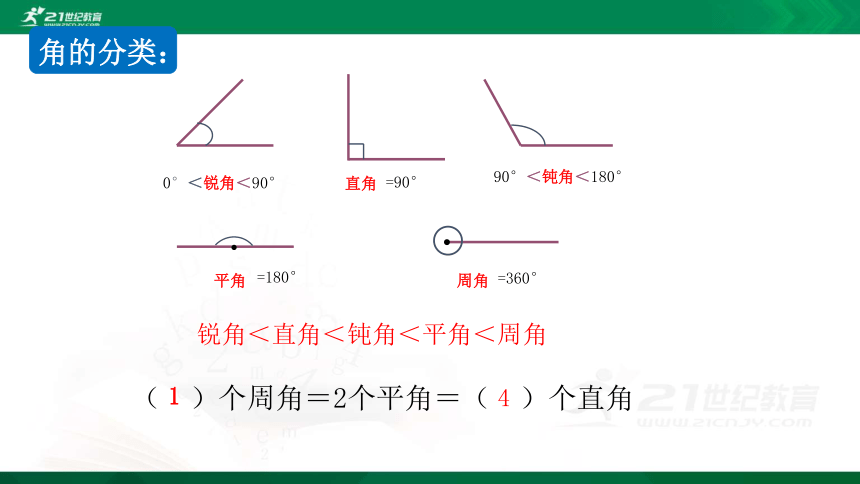
0°<锐角<90°
90°<钝角<180°
周角
直角
=90°
平角
=180°
=360°
( )个周角=2个平角=( )个直角
1
4
锐角<直角<钝角<平角<周角
角的分类:
:由三条线段围成的封闭图形叫做三角形。
:三角形具有稳定性(不易变形)。
底
高
三角形:
关于三角形,你知道些什么?
:三角形的内角和等于180°。
:三角形的任意两边之和大于第三边。
:从三角形一个顶点向它的对边作一条垂线,顶
点和垂足之间的线段称三角形这条边上的高。
三角形
:三角形有3条边,3个顶点,3个角,3条高。
定义
组成
高
内角和
三边关系
特征
分类
按角分
按边分
三角形按角分
三角形的分类:
钝角
三角形
直角
三角形
锐角
三角形
三角形
三角形按边分
等腰三角形
等边三角形
等腰三角形
腰
腰
底
顶角
底角
底角
腰
顶角
腰
底角
底角
底
等腰直角三角形
腰
腰
底
顶角
底角
底角
等腰三角形
有两条边相等的三角形叫做等腰三角形。其中相等的两条边叫做腰,另一条叫做底。两条腰的夹角叫做顶角,腰和底的夹角叫做底角,等腰三角形的两个底角度数相等。
等腰三角形:
边
边
边
等边三角形
(正三角形)
三条边都相等的三角形叫做等边三角形,又叫正三角形。等边三角形的三条边长度相等,三个角的大小相等,都是60°。
等边三角形是特殊的等腰三角形。
等边三角形:
60°
60°
60°
我们学过哪些四边形?
平行四边形
长方形
正方形
梯形
不规则四边形
它们有哪些特征?
底
高
平行四边形
高
底
平行四边形:
关于平行四边形,你知道些什么?
特征
高
:从平行四边形一条边上的一点向对边引一条垂线,这点
和垂足之间的线段叫做平行四边形的高,这条边叫做平
行四边形的底。
定义
:两组对边分别平行的四边形叫做平行四边形。
:平行四边形对边平行,对边长度相等,对角大小相等。
:平行四边形具有不稳定性(容易变形)。
两组对边分别平行并且相等,四个角都是直角的四边形叫做长方形。
长方形中较长的一组对边叫做长方形的长,较短的一组对边叫做长方形的宽。
长方形是特殊的平行四边形。
长
长方形
长方形
宽
宽
长
长方形
正方形
四条边相等,四个角都是直角的四边形叫做正方形。
正方形是特殊的长方形。
正方形
两腰相等的梯形叫做等腰梯形。
上底
下底
腰
腰
高
等腰梯形
直角梯形
梯形
定义:只有一组对边平行的四边形叫做梯形。
组成:在梯形里,互相平行的一组对边叫做梯形的
上底和下底,不平行的一组叫做梯形的腰,
上底和下底之间的距离叫做梯形的高。
有一个直角的梯形叫做直角梯形。
四边形
两组对边
分别平行
有一个角是直角
邻边相等
有一个角是直角且邻边相等
只有一组对边平行
等腰梯形
两腰相等
有一个角是直角
两组对边都不平行
直角梯形
长方形
平行四边形
正方形
梯形
四边形
两组对边
分别平行
有一个角是直角
邻边相等
有一个角是直角且邻边相等
只有一组对边平行
等腰梯形
两腰相等
有一个角是直角
两组对边都不平行
直角梯形
长方形
平行四边形
正方形
梯形
圆与上面的平面图形有什么不同?圆有哪些特点?
·
O
圆心
半径r
直径d
·
圆是平面上由曲线围成的封闭图形。
连接圆心和圆上任意一点的线段叫做圆的半径。
圆内有无数条半径和直径。同圆或等圆中,所有的直径长度相等,所有的半径长度也相等,且直径长度是半径的2倍。d=2r或者r=
圆是轴对称图形,圆有无数条对称轴,即为直径所在的直线。
圆心决定圆的位置,半径决定圆的大小。
通过圆心且两端都在圆上的线段叫做圆的直径。
封闭图形一周的长度,叫做它的周长。
你能举例说明什么是图形的周长和面积吗?
周长常用的长度单位:
常用的面积单位:
数学书封面一周的长度就是它的周长。
数学书封面表面的大小就是它的面积。
物体的表面或围成平面图形的大小,叫做它的面积。
厘米、分米、米等。
平方米、平方分米、平方厘米等。
2(a+b)
ab
4a
a2
ah
ah÷2
(a+b)h÷2
2πr
πr2
写出下面图形的周长和面积计算公式(用字母表示)。
最早学习的是哪个图形的周长和面积的计算?
长
宽
长方形的面积=
长方形的周长=(长+宽)×2
长×宽
S=ab
C=(a+b)×2
a
b
正方形与长方形有什么关系?
正方形的面积=
正方形的周长=边长×4
S=
边长×边长
边长
边长
a
a
S=a
C=4a
底
高
平行四边形的面积=
S=
底×高
平行四边形的面积公式是怎样推导出来的呢?
平行四边形的底等于长方形
的长,高等于长方形的宽。
高
底
两个完全一样的三角形可以拼成一个平行四边形。
三角形的面积=
底×高÷2
S=ah÷2
三角形的面积等于与它等底等高的平行四边形面积的一半。
两个完全相同的梯形可以拼成一个平行四边形。
梯形的面积等于与它等底等高的平
行四边形面积的一半。
梯形的面积=(上底+下底)×高÷2
高
下底
上底
a
b
S=(a+b)h÷2
长
宽
把圆切割成若干偶数等份,拼接成近似长方形。
=πr
=r
S=πr
圆的面积:
圆的周长:
C=2πr=πd
数 学 训 练 营
一.我会填!
1.三角形三个角度数的比是1:2:3,最大的角是( )。
2.一个平行四边形和一个三角形等底等高。已知平行四边形的
面积是30 cm ,则三角形的面积等于( )cm 。
直角
15
任意一个三角形的内角和都等于180°。
90°
三角形的面积等于与它等底等高的平行四边形面积的一半。
3.圆的半径扩大到原来的2倍,面积扩大到原来的( )倍。
4
假设r=1cm
S=πr
=3.14×1
=3.14(cm )
r=2cm
3.14×2
=3.14×4
=12.56(cm )
12.56÷3.14=4
1.大于90°的角就是钝角。 ( )
2.两条直线相交组成的4个角中,如果有一个是直角,那么其他
三个角也是直角。 ( )
3.任何两个等底等高的梯形都能拼成一个平行四边形。( )
×
√
两条直线互相垂直
完全相同
×
二.我会判!对的画“√”,错的画“×”。
90°<钝角<180°
4.半径是2厘米的圆,周长和面积相等。 ( )
×
5.长度为1cm、2.5cm、3cm的线段可以围成一个三角形。( )
两边之和大于第三边。
√
周长和面积的意义不同,单位不同,不是同一类,不能比较大小。
计算下面各图形的周长和面积。(单位:cm)
三角形的面积=底×高÷2
面积:30×40÷2=600(cm )
周长:30+40+50=120(cm)
40
30
50
三.我会算!
3.14×(4÷2) ÷2 =3.14×4÷2
=6.28(cm )
3.14×4÷2+4
=6.28+4
=10.28(cm)
·
d=4cm
S半圆=πr ÷2
C半圆=πd÷2+d
有一圆形蓄水池,它的周长是31.4m,它的占地面积约是多少?
先求出圆形水池的半径。
半径:31.4÷3.14÷2
=10÷2
=5(m)
求圆形水池的面积。
面积:3.14×5
=3.14×25
=78.5(m )
答:它的占地面积是78.5平方米。
四.我会解决问题!
通过这节课的学习,你有什么收获?
1.全面掌握小学阶段所学的平面图形的基本特征,能画出相应的图形;能正确计算平面图形的周长与面积,并能运用相关知识解决生活中的实际问题。
2.通过分类、比较、辨析,进一步认识图形的区别与联系,形成清晰的知识网络。
3.通过整理和复习,借助几何图形的直观性,增强我们的空间观念和空间想象能力。
学习目标:
你完成今天的学习目标了吗?
平面图形
线
线段
直线
射线
两条直线的位置关系
(同一平面内)
平行→平行线
相交→互相垂直→垂线
角
锐角
直角
钝角
平角
周角
三角形
四边形
圆
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
等腰三角形→等边三角形
一般四边形
平行四边形 长方形 正方形
梯形
一般梯形
等腰梯形
直角梯形
四个角
是直角
四条边
都相等
轴对称图形
2(a+b)
ab
4a
a2
ah
ah÷2
(a+b)h÷2
2πr
πr2
平面图形的周长和面积计算公式
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第六单元 整理与复习 2.图形与几何
图形的认识与测量(例1—3)
数学人教版 六年级下
1.全面掌握小学阶段所学的平面图形的基本特征,能画出相应的
图形;能正确计算平面图形的周长与面积,并能运用相关知识解
决生活中的实际问题。
2.通过分类、比较、辨析,进一步认识图形的区别与联系,形成
清晰的知识网络。
3.通过整理与复习,借助几何图形的直观性,增强我们的空间观
念和空间想象能力。
学习目标:
平
面
图
形
三角形
按角分
直角三角形
钝角三角形
按边分
不等边三角形
等边三角形
等腰三角形
四边形
平行四边形
四个角
是直角
长方形
四条边
都相等
正方形
梯形
等腰梯形
直角梯形
圆
轴对称图形
图形
锐角三角形
立体图形
长方体
正方体
圆柱
圆锥
想一想,我们都学过哪些平面图形与立体图形?怎样把图形分类。
直线、射线和线段有什么区别和联系?
●
●
●
线段:
射线:
直线:
用直尺把两点连接起来,就得到一条线段;
把线段一端无限延长,可以得到一条射线;
把线段两端无限延长,可以得到一条直线。
名称 图示 端点数量 延长性 能否度量 长度比较
直线
射线
线段
没有
一个
两个
可向两端
无限延长
可向一端
无限延长
不能向两
端延长
长度不能度量
长度不能度量
长度能度量
无限长,不能比较
无限长,不
能比较
有限长,能比较
直线、射线和线段的联系和区别:
●
●
●
直线、射线和线段都是直的。
经过一点可以画无数条直线。
从一点可以引出无数条射线。
经过两点只可以画一条直线,两点确定一条直线。
重要的“点”:
同一平面内的两条直线有哪几种位置关系?
同一平面内的两条直线的位置关系:平行或相交。
同一平面内永不相交的两条直线叫做平行线,也可以说两条直线互相平行。
相交
互相平行
交点
两条直线相交成直角时,这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
相交
垂足
互相垂直
交点
a
b
a∥b
a⊥b
b
a
A
直线a与b互相垂直,记作a⊥b,读作a垂直于b。
a
b
作垂线的方法:
连接两点之间的线段的长度,就是这两点之间的距离。两点之间线段最短。
②
①
③
1.小白兔去采蘑菇,它会选择哪条路呢?为什么?
练一练:
②
①
③
从直线外一点到这条直线所画的垂直线段最短,它的长度叫做点到直线的距离。
两条平行线间的距离处处相等。
2.村民们要修一条水渠与小河相通,要使水渠最短,应该怎样挖?
一组平行线之间的距离,垂直线段最短。
练一练:
水 渠
从一点引出的两条射线所组成的图形叫做角。
顶点
边
边
这个点叫做角的顶点,这两条射线叫做角的边,角通常用符号“∠”来表示。
角的大小要看两边叉开的大小,开口越大,角越大。角的大小与两条边的长短无关。
我们学过哪些角?角的大小和什么有关?
在放大镜下看角,角的大小不变。
1
∠1
0°<锐角<90°
90°<钝角<180°
周角
直角
=90°
平角
=180°
=360°
( )个周角=2个平角=( )个直角
1
4
锐角<直角<钝角<平角<周角
角的分类:
:由三条线段围成的封闭图形叫做三角形。
:三角形具有稳定性(不易变形)。
底
高
三角形:
关于三角形,你知道些什么?
:三角形的内角和等于180°。
:三角形的任意两边之和大于第三边。
:从三角形一个顶点向它的对边作一条垂线,顶
点和垂足之间的线段称三角形这条边上的高。
三角形
:三角形有3条边,3个顶点,3个角,3条高。
定义
组成
高
内角和
三边关系
特征
分类
按角分
按边分
三角形按角分
三角形的分类:
钝角
三角形
直角
三角形
锐角
三角形
三角形
三角形按边分
等腰三角形
等边三角形
等腰三角形
腰
腰
底
顶角
底角
底角
腰
顶角
腰
底角
底角
底
等腰直角三角形
腰
腰
底
顶角
底角
底角
等腰三角形
有两条边相等的三角形叫做等腰三角形。其中相等的两条边叫做腰,另一条叫做底。两条腰的夹角叫做顶角,腰和底的夹角叫做底角,等腰三角形的两个底角度数相等。
等腰三角形:
边
边
边
等边三角形
(正三角形)
三条边都相等的三角形叫做等边三角形,又叫正三角形。等边三角形的三条边长度相等,三个角的大小相等,都是60°。
等边三角形是特殊的等腰三角形。
等边三角形:
60°
60°
60°
我们学过哪些四边形?
平行四边形
长方形
正方形
梯形
不规则四边形
它们有哪些特征?
底
高
平行四边形
高
底
平行四边形:
关于平行四边形,你知道些什么?
特征
高
:从平行四边形一条边上的一点向对边引一条垂线,这点
和垂足之间的线段叫做平行四边形的高,这条边叫做平
行四边形的底。
定义
:两组对边分别平行的四边形叫做平行四边形。
:平行四边形对边平行,对边长度相等,对角大小相等。
:平行四边形具有不稳定性(容易变形)。
两组对边分别平行并且相等,四个角都是直角的四边形叫做长方形。
长方形中较长的一组对边叫做长方形的长,较短的一组对边叫做长方形的宽。
长方形是特殊的平行四边形。
长
长方形
长方形
宽
宽
长
长方形
正方形
四条边相等,四个角都是直角的四边形叫做正方形。
正方形是特殊的长方形。
正方形
两腰相等的梯形叫做等腰梯形。
上底
下底
腰
腰
高
等腰梯形
直角梯形
梯形
定义:只有一组对边平行的四边形叫做梯形。
组成:在梯形里,互相平行的一组对边叫做梯形的
上底和下底,不平行的一组叫做梯形的腰,
上底和下底之间的距离叫做梯形的高。
有一个直角的梯形叫做直角梯形。
四边形
两组对边
分别平行
有一个角是直角
邻边相等
有一个角是直角且邻边相等
只有一组对边平行
等腰梯形
两腰相等
有一个角是直角
两组对边都不平行
直角梯形
长方形
平行四边形
正方形
梯形
四边形
两组对边
分别平行
有一个角是直角
邻边相等
有一个角是直角且邻边相等
只有一组对边平行
等腰梯形
两腰相等
有一个角是直角
两组对边都不平行
直角梯形
长方形
平行四边形
正方形
梯形
圆与上面的平面图形有什么不同?圆有哪些特点?
·
O
圆心
半径r
直径d
·
圆是平面上由曲线围成的封闭图形。
连接圆心和圆上任意一点的线段叫做圆的半径。
圆内有无数条半径和直径。同圆或等圆中,所有的直径长度相等,所有的半径长度也相等,且直径长度是半径的2倍。d=2r或者r=
圆是轴对称图形,圆有无数条对称轴,即为直径所在的直线。
圆心决定圆的位置,半径决定圆的大小。
通过圆心且两端都在圆上的线段叫做圆的直径。
封闭图形一周的长度,叫做它的周长。
你能举例说明什么是图形的周长和面积吗?
周长常用的长度单位:
常用的面积单位:
数学书封面一周的长度就是它的周长。
数学书封面表面的大小就是它的面积。
物体的表面或围成平面图形的大小,叫做它的面积。
厘米、分米、米等。
平方米、平方分米、平方厘米等。
2(a+b)
ab
4a
a2
ah
ah÷2
(a+b)h÷2
2πr
πr2
写出下面图形的周长和面积计算公式(用字母表示)。
最早学习的是哪个图形的周长和面积的计算?
长
宽
长方形的面积=
长方形的周长=(长+宽)×2
长×宽
S=ab
C=(a+b)×2
a
b
正方形与长方形有什么关系?
正方形的面积=
正方形的周长=边长×4
S=
边长×边长
边长
边长
a
a
S=a
C=4a
底
高
平行四边形的面积=
S=
底×高
平行四边形的面积公式是怎样推导出来的呢?
平行四边形的底等于长方形
的长,高等于长方形的宽。
高
底
两个完全一样的三角形可以拼成一个平行四边形。
三角形的面积=
底×高÷2
S=ah÷2
三角形的面积等于与它等底等高的平行四边形面积的一半。
两个完全相同的梯形可以拼成一个平行四边形。
梯形的面积等于与它等底等高的平
行四边形面积的一半。
梯形的面积=(上底+下底)×高÷2
高
下底
上底
a
b
S=(a+b)h÷2
长
宽
把圆切割成若干偶数等份,拼接成近似长方形。
=πr
=r
S=πr
圆的面积:
圆的周长:
C=2πr=πd
数 学 训 练 营
一.我会填!
1.三角形三个角度数的比是1:2:3,最大的角是( )。
2.一个平行四边形和一个三角形等底等高。已知平行四边形的
面积是30 cm ,则三角形的面积等于( )cm 。
直角
15
任意一个三角形的内角和都等于180°。
90°
三角形的面积等于与它等底等高的平行四边形面积的一半。
3.圆的半径扩大到原来的2倍,面积扩大到原来的( )倍。
4
假设r=1cm
S=πr
=3.14×1
=3.14(cm )
r=2cm
3.14×2
=3.14×4
=12.56(cm )
12.56÷3.14=4
1.大于90°的角就是钝角。 ( )
2.两条直线相交组成的4个角中,如果有一个是直角,那么其他
三个角也是直角。 ( )
3.任何两个等底等高的梯形都能拼成一个平行四边形。( )
×
√
两条直线互相垂直
完全相同
×
二.我会判!对的画“√”,错的画“×”。
90°<钝角<180°
4.半径是2厘米的圆,周长和面积相等。 ( )
×
5.长度为1cm、2.5cm、3cm的线段可以围成一个三角形。( )
两边之和大于第三边。
√
周长和面积的意义不同,单位不同,不是同一类,不能比较大小。
计算下面各图形的周长和面积。(单位:cm)
三角形的面积=底×高÷2
面积:30×40÷2=600(cm )
周长:30+40+50=120(cm)
40
30
50
三.我会算!
3.14×(4÷2) ÷2 =3.14×4÷2
=6.28(cm )
3.14×4÷2+4
=6.28+4
=10.28(cm)
·
d=4cm
S半圆=πr ÷2
C半圆=πd÷2+d
有一圆形蓄水池,它的周长是31.4m,它的占地面积约是多少?
先求出圆形水池的半径。
半径:31.4÷3.14÷2
=10÷2
=5(m)
求圆形水池的面积。
面积:3.14×5
=3.14×25
=78.5(m )
答:它的占地面积是78.5平方米。
四.我会解决问题!
通过这节课的学习,你有什么收获?
1.全面掌握小学阶段所学的平面图形的基本特征,能画出相应的图形;能正确计算平面图形的周长与面积,并能运用相关知识解决生活中的实际问题。
2.通过分类、比较、辨析,进一步认识图形的区别与联系,形成清晰的知识网络。
3.通过整理和复习,借助几何图形的直观性,增强我们的空间观念和空间想象能力。
学习目标:
你完成今天的学习目标了吗?
平面图形
线
线段
直线
射线
两条直线的位置关系
(同一平面内)
平行→平行线
相交→互相垂直→垂线
角
锐角
直角
钝角
平角
周角
三角形
四边形
圆
按角分
锐角三角形
直角三角形
钝角三角形
按边分
不等边三角形
等腰三角形→等边三角形
一般四边形
平行四边形 长方形 正方形
梯形
一般梯形
等腰梯形
直角梯形
四个角
是直角
四条边
都相等
轴对称图形
2(a+b)
ab
4a
a2
ah
ah÷2
(a+b)h÷2
2πr
πr2
平面图形的周长和面积计算公式
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
