六年级下册数学等级训练试题-第7周正比例和反比例(含答案)人教版
文档属性
| 名称 | 六年级下册数学等级训练试题-第7周正比例和反比例(含答案)人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 783.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-28 14:56:02 | ||
图片预览


文档简介
六年级 第7周 一级监测卷
监测内容:正比例和反比例
时间:40分钟 满分100分
填一填。(每空2分,共24分)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的( )一定,这两种量就叫做成正比例的量。如果用字母y和x表示两种相关的量,用k表示它们的比值(一定),正比例关系可以用式子表示,这个式子是( )。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做( )的量。如果用字母x和y表示两种相关的量,用k表示它们的积(一定),反比例关系可以用式子表示,这个式子是( )。
(3)因为=速度(一定),所以( )和( )成( )比例;因为( )×( )=路程(一定),所以( )和( )成( )比例。
二、如果ab=c,那么(每空4分,共12分)
(1)当a一定时,b和c成( )比例。
(2)当c一定时,a和b成( )比例。
(3)当b一定时,a和c成( )比例。
三、下面各题中的两种量是否成比例关系,如果成比例关系,成什么比例关系?(每空4分,共32分)
(1)120名同学参加团体体操表演,每排的人数和排数。 ( )
(2)花生的出油率一定,花生的出油量和花生的质量。 ( )
(3)用同样大的正方形地砖铺地,地砖的块数和铺地的面积。 ( )
(4)一个商场每天的营业时间一定,每天接待顾客的数量与营业额。 ( )
(5)行驶的路程一定,车轮的周长与车轮需要转动的圈数。 ( )
(6)一条公路,已经修了的米数与没有修的米数。 ( )
(7)梯形的面积一定,它的上下底的和与高。 ( )
(8)y=x ( )
四、一个啤酒厂生产情况记录表如下。(共20分)
工作时间(时)
1
2
3
4
5
6
工作总量(吨)
20
40
60
80
100
120
①写出几组工作总量与相对应的工作时间的比,并比较比值的大小。(4分)
②这个比值表示( )。(3分)
③工作总量与工作时间成正比例关系吗?为什么?(3分)
④在下图中把表中工作时间和工作总量所对应的点描出来,并按顺序把它们连接起来。再根据图象估计一下,3.5小时能生产啤酒( );要生产150吨啤酒需要( )小时。(10分)
载质量/t
2.5
4
5
6
8
10
数量/辆
48
30
24
20
15
12
五、运输公司要将一批物资运往某地。车辆载质量与所需车辆的数量如下表。(共12分)
①根据上表的信息,你能算出这批物资一共有多少吨吗?(3分)
②汽车载质量Z表示,需要汽车的数量用S表示,这批物资的质量用n表示。用式子表示Z、S、n之间的关系为( )。(3分)
③Z和S成什么比例关系?为什么?(3分)
④如果这批物资用载质量为7.5吨的汽车一次运完,需要( )辆汽车来运。(3分)
六年级 第7周 二级监测卷
监测内容:正比例和反比例
时间:40分钟 满分100分
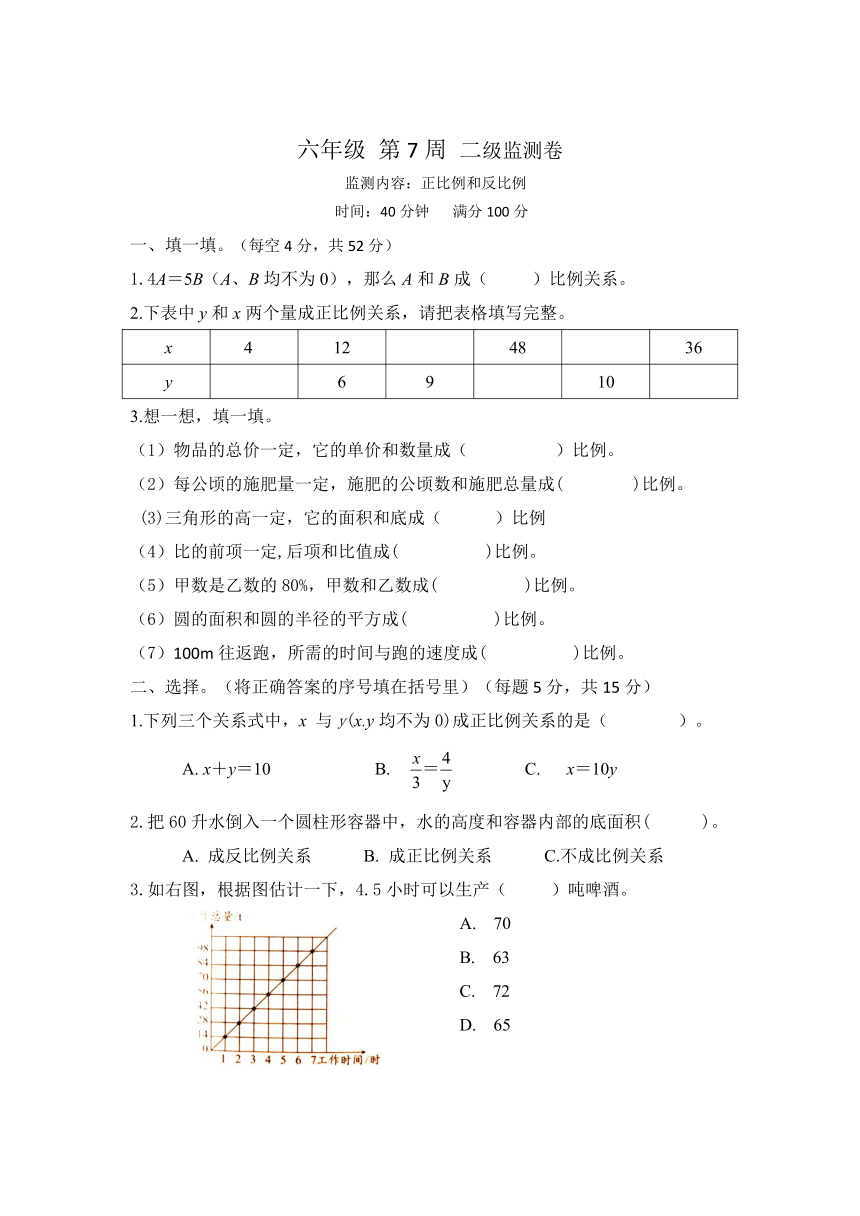
一、填一填。(每空4分,共52分)
1.4A=5B(A、B均不为0),那么A和B成( )比例关系。
2.下表中y和x两个量成正比例关系,请把表格填写完整。
x
4
12
48
36
y
6
9
10
3.想一想,填一填。
(1)物品的总价一定,它的单价和数量成( )比例。 (2)每公顷的施肥量一定,施肥的公顷数和施肥总量成( )比例。 (3)三角形的高一定,它的面积和底成( )比例 (4)比的前项一定,后项和比值成( )比例。
(5)甲数是乙数的80%,甲数和乙数成( )比例。
(6)圆的面积和圆的半径的平方成( )比例。
(7)100m往返跑,所需的时间与跑的速度成( )比例。
二、选择。(将正确答案的序号填在括号里)(每题5分,共15分)
1.下列三个关系式中,x 与y(x.y均不为0)成正比例关系的是( )。
A. x+y=10 B. C. x=10y
2.把60升水倒入一个圆柱形容器中,水的高度和容器内部的底面积( ?)。 A. 成反比例关系 B. 成正比例关系 C.不成比例关系
3.如右图,根据图估计一下,4.5小时可以生产( )吨啤酒。
A. 70
B. 63
C. 72
D. 65
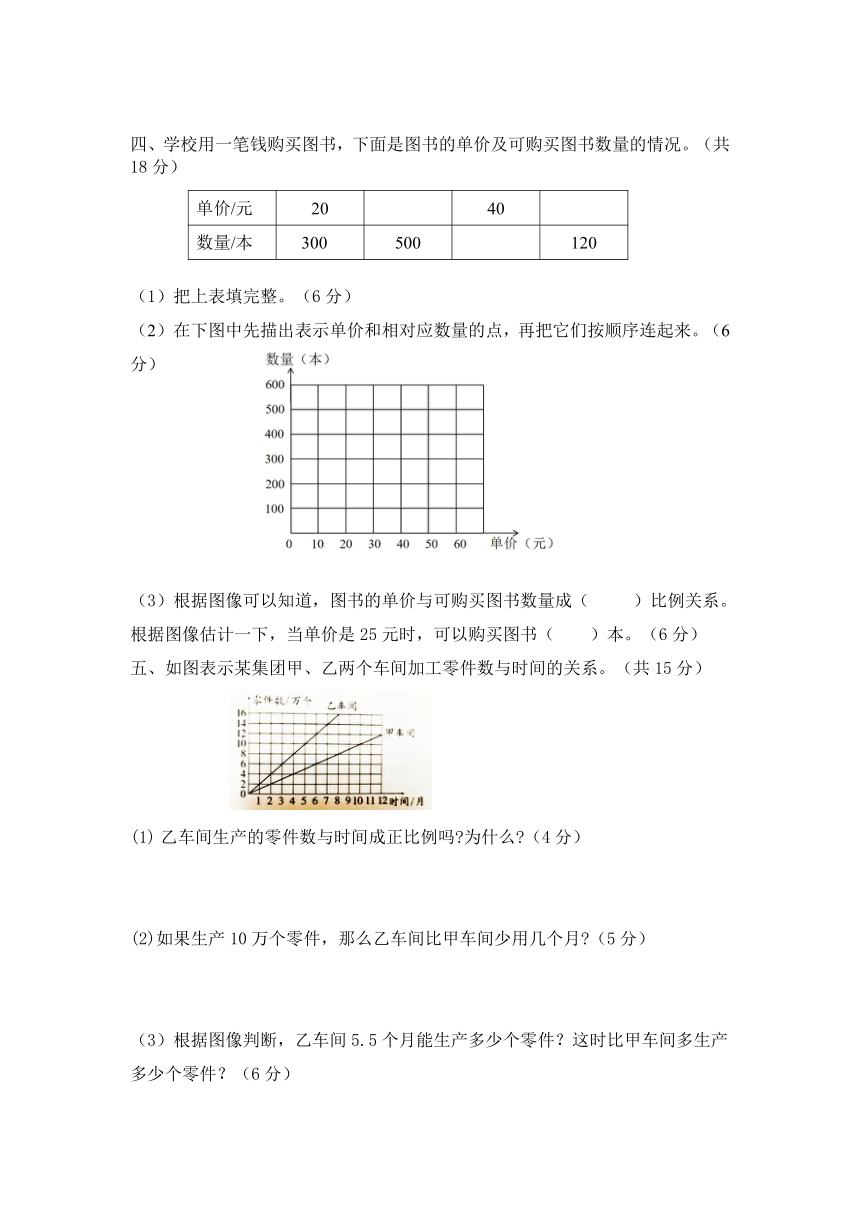
四、学校用一笔钱购买图书,下面是图书的单价及可购买图书数量的情况。(共18分)
单价/元
20
40
数量/本
300
500
120
把上表填完整。(6分)
在下图中先描出表示单价和相对应数量的点,再把它们按顺序连起来。(6分)
根据图像可以知道,图书的单价与可购买图书数量成( )比例关系。
根据图像估计一下,当单价是25元时,可以购买图书( )本。(6分)
如图表示某集团甲、乙两个车间加工零件数与时间的关系。(共15分)
乙车间生产的零件数与时间成正比例吗?为什么?(4分)
(2)如果生产10万个零件,那么乙车间比甲车间少用几个月?(5分)
(3)根据图像判断,乙车间5.5个月能生产多少个零件?这时比甲车间多生产多少个零件?(6分)
六年级 第7周 一级监测卷
监测内容:正比例和反比例
时间:40分钟 满分100分
一、填一填。(每空2分,共24分)
(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的( 比值 )一定,这两种量就叫做成正比例的量。如果用字母y和x表示两种相关的量,用k表示它们的比值(一定),正比例关系可以用式子表示,这个式子是( =k )。
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做( 成反比例 )的量。如果用字母x和y表示两种相关的量,用k表示它们的积(一定),反比例关系可以用式子表示,这个式子是( xy=k )。
(3)因为 =速度(一定),所以( 路程 )和( 时间 )成(正 )比例;因为(速度 )×(时间)=路程(一定),所以(速度 )和(时间 )成( 反)比例。
二、如果ab=c,那么(每空4分,共12分)
(1)当a一定时,b和c成( 正 )比例。
(2)当c一定时,a和b成( 反)比例。
(3)当b一定时,a和c成( 正)比例。
三、下面各题中的两种量是否成比例关系,如果成比例关系,成什么比例关系?(每空4分,共32分)
(1)120名同学参加团体体操表演,每排的人数和排数。 (成反比例关系 )
(2)花生的出油率一定,花生的出油量和花生的质量。 ( 成正比例关系 )
(3)用同样大的正方形地砖铺地,地砖的块数和铺地的面积。(成正比例关系 )
(4)一个商场每天的营业时间一定,每天接待顾客的数量与营业额。 (不成比例关系 )
(5)行驶的路程一定,车轮的周长与车轮需要转动的圈数。 (成反比例关系)
(6)一条公路,已经修了的米数与没有修的米数。 (不成比例关系 )
(7)梯形的面积一定,它的上下底的和与高。 ( 成反比例关系 )
(8)y=x (成正比例关系 )
四、一个啤酒厂生产情况记录表如下。(共20分)
工作时间(时)
1
2
3
4
5
6
工作总量(吨)
20
40
60
80
100
120
①写出几组工作总量与相对应的工作时间的比,并比较比值的大小。(4分)
……
②这个比值表示(工作效率)。(3分)
③工作总量与工作时间成正比例关系吗?为什么?(3分)
答:工作总量与工作时间成正比例关系,因为。
④在下图中把表中工作时间和工作总量所对应的点描出来,并按顺序把它们连接起来。再根据图象估计一下,3.5小时能生产啤酒( 70吨 );要生产150吨啤酒需要( 7.5 )小时。(10分)
载质量/t
2.5
4
5
6
8
10
数量/辆
48
30
24
20
15
12
五、运输公司要将一批物资运往某地。车辆载质量与所需车辆的数量如下表。(共12分)
①根据上表的信息,你能算出这批物资一共有多少吨吗?(3分)
2.5×48=120(吨)
答:这批物资一共有120吨。
②汽车载质量z表示,需要汽车的数量用s表示,这批物资的质量用N表示。用式子表示z、s、N之间的关系为( N=zs )。(3分)
③z和s成什么比例关系?为什么?(3分)
2.5×48=4×30=5×24=6×20=8×15=10×12
答:z和s成反比例关系,因为汽车载质量×需要汽车的数量=这批物资的质量(一定)。
④如果这批物资用载质量为7.5吨的汽车一次运完,需要(16)辆汽车来运。(3分)
120÷7.5=16(辆)
六年级 第7周 二级监测卷
监测内容:正比例和反比例
时间:40分钟 满分100分
一、填一填。(每空4分,共52分)
1.4A=5B(A、B均不为0),那么A和B成( 正 )比例关系。
2.下表中y和x两个量成正比例关系,请把表格填写完整。
x
4
12
18
48
20
36
y
2
6
9
24
10
18
3.想一想,填一填。
(1)物品的总价一定,它的单价和数量成(反)比例。 (2)每公顷的施肥量一定,施肥的公顷数和施肥总量成( 正 )比例。 (3)三角形的高一定,它的面积和底成(正)比例 (4)比的前项一定,后项和比值成( 反 )比例。
(5)甲数是乙数的80%,甲数和乙数成( 正 )比例。
(6)圆的面积和圆的半径的平方成( 正 )比例。
(7)100m往返跑,所需的时间与跑的速度成( 反 )比例。
二、选择。(将正确答案的序号填在括号里)(每题5分,共15分)
1.下列三个关系式中,x 与y(x.y均不为0)成正比例关系的是( C )。
A. x+y=10 B. C. x=10y
2.把60升水倒入一个圆柱形容器中,水的高度和容器内部的底面积( A?)。 A. 成反比例关系 B. 成正比例关系 C.不成比例关系
3.如右图,根据图估计一下,4.5小时可以生产( B )吨啤酒。
A. 70
B. 63
C. 72
D. 65
四、学校用一笔钱购买图书,下面是图书的单价及可购买图书数量的情况。(共18分)
单价/元
20
12
40
50
数量/本
300
500
150
120
(1)把上表填完整。(6分)
(2)在下图中先描出表示单价和相对应数量的点,再把它们按顺序连起来。(6分)
(3)根据图像可以知道,图书的单价与可购买图书数量成(反 )比例关系。
根据图像估计一下,当单价是25元时,可以购买图书(240)本。(6分)
如图表示某集团甲、乙两个车间加工零件数与时间的关系。(共15分)
(1)乙车间生产的零件数与时间成正比例吗?为什么?(4分)
答:乙车间生产的零件数与时间成正比例,因为。 (2)如果生产10万个零件,那么乙车间比甲车间少用几个月?(5分)
10÷(2÷1)=5(个) 10÷(4÷4)=10(个) 10-5=5(个)
答:乙车间比甲车间少用5个月。
(3)根据图像判断,乙车间5.5个月能生产多少个零件?这时比甲车间多生产多少个零件?(6分)
5.5×2=11(万个)
5.5×1=5.5(万个)
11-5.5=5.5(万个)
或5.5×(2-1)=5.5(万个)
答:乙车间5.5个月能生产11万个零件,这时比甲车间多生产5.5万个零件。
监测内容:正比例和反比例
时间:40分钟 满分100分
填一填。(每空2分,共24分)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的( )一定,这两种量就叫做成正比例的量。如果用字母y和x表示两种相关的量,用k表示它们的比值(一定),正比例关系可以用式子表示,这个式子是( )。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做( )的量。如果用字母x和y表示两种相关的量,用k表示它们的积(一定),反比例关系可以用式子表示,这个式子是( )。
(3)因为=速度(一定),所以( )和( )成( )比例;因为( )×( )=路程(一定),所以( )和( )成( )比例。
二、如果ab=c,那么(每空4分,共12分)
(1)当a一定时,b和c成( )比例。
(2)当c一定时,a和b成( )比例。
(3)当b一定时,a和c成( )比例。
三、下面各题中的两种量是否成比例关系,如果成比例关系,成什么比例关系?(每空4分,共32分)
(1)120名同学参加团体体操表演,每排的人数和排数。 ( )
(2)花生的出油率一定,花生的出油量和花生的质量。 ( )
(3)用同样大的正方形地砖铺地,地砖的块数和铺地的面积。 ( )
(4)一个商场每天的营业时间一定,每天接待顾客的数量与营业额。 ( )
(5)行驶的路程一定,车轮的周长与车轮需要转动的圈数。 ( )
(6)一条公路,已经修了的米数与没有修的米数。 ( )
(7)梯形的面积一定,它的上下底的和与高。 ( )
(8)y=x ( )
四、一个啤酒厂生产情况记录表如下。(共20分)
工作时间(时)
1
2
3
4
5
6
工作总量(吨)
20
40
60
80
100
120
①写出几组工作总量与相对应的工作时间的比,并比较比值的大小。(4分)
②这个比值表示( )。(3分)
③工作总量与工作时间成正比例关系吗?为什么?(3分)
④在下图中把表中工作时间和工作总量所对应的点描出来,并按顺序把它们连接起来。再根据图象估计一下,3.5小时能生产啤酒( );要生产150吨啤酒需要( )小时。(10分)
载质量/t
2.5
4
5
6
8
10
数量/辆
48
30
24
20
15
12
五、运输公司要将一批物资运往某地。车辆载质量与所需车辆的数量如下表。(共12分)
①根据上表的信息,你能算出这批物资一共有多少吨吗?(3分)
②汽车载质量Z表示,需要汽车的数量用S表示,这批物资的质量用n表示。用式子表示Z、S、n之间的关系为( )。(3分)
③Z和S成什么比例关系?为什么?(3分)
④如果这批物资用载质量为7.5吨的汽车一次运完,需要( )辆汽车来运。(3分)
六年级 第7周 二级监测卷
监测内容:正比例和反比例
时间:40分钟 满分100分
一、填一填。(每空4分,共52分)
1.4A=5B(A、B均不为0),那么A和B成( )比例关系。
2.下表中y和x两个量成正比例关系,请把表格填写完整。
x
4
12
48
36
y
6
9
10
3.想一想,填一填。
(1)物品的总价一定,它的单价和数量成( )比例。 (2)每公顷的施肥量一定,施肥的公顷数和施肥总量成( )比例。 (3)三角形的高一定,它的面积和底成( )比例 (4)比的前项一定,后项和比值成( )比例。
(5)甲数是乙数的80%,甲数和乙数成( )比例。
(6)圆的面积和圆的半径的平方成( )比例。
(7)100m往返跑,所需的时间与跑的速度成( )比例。
二、选择。(将正确答案的序号填在括号里)(每题5分,共15分)
1.下列三个关系式中,x 与y(x.y均不为0)成正比例关系的是( )。
A. x+y=10 B. C. x=10y
2.把60升水倒入一个圆柱形容器中,水的高度和容器内部的底面积( ?)。 A. 成反比例关系 B. 成正比例关系 C.不成比例关系
3.如右图,根据图估计一下,4.5小时可以生产( )吨啤酒。
A. 70
B. 63
C. 72
D. 65
四、学校用一笔钱购买图书,下面是图书的单价及可购买图书数量的情况。(共18分)
单价/元
20
40
数量/本
300
500
120
把上表填完整。(6分)
在下图中先描出表示单价和相对应数量的点,再把它们按顺序连起来。(6分)
根据图像可以知道,图书的单价与可购买图书数量成( )比例关系。
根据图像估计一下,当单价是25元时,可以购买图书( )本。(6分)
如图表示某集团甲、乙两个车间加工零件数与时间的关系。(共15分)
乙车间生产的零件数与时间成正比例吗?为什么?(4分)
(2)如果生产10万个零件,那么乙车间比甲车间少用几个月?(5分)
(3)根据图像判断,乙车间5.5个月能生产多少个零件?这时比甲车间多生产多少个零件?(6分)
六年级 第7周 一级监测卷
监测内容:正比例和反比例
时间:40分钟 满分100分
一、填一填。(每空2分,共24分)
(1)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的( 比值 )一定,这两种量就叫做成正比例的量。如果用字母y和x表示两种相关的量,用k表示它们的比值(一定),正比例关系可以用式子表示,这个式子是( =k )。
(2)两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做( 成反比例 )的量。如果用字母x和y表示两种相关的量,用k表示它们的积(一定),反比例关系可以用式子表示,这个式子是( xy=k )。
(3)因为 =速度(一定),所以( 路程 )和( 时间 )成(正 )比例;因为(速度 )×(时间)=路程(一定),所以(速度 )和(时间 )成( 反)比例。
二、如果ab=c,那么(每空4分,共12分)
(1)当a一定时,b和c成( 正 )比例。
(2)当c一定时,a和b成( 反)比例。
(3)当b一定时,a和c成( 正)比例。
三、下面各题中的两种量是否成比例关系,如果成比例关系,成什么比例关系?(每空4分,共32分)
(1)120名同学参加团体体操表演,每排的人数和排数。 (成反比例关系 )
(2)花生的出油率一定,花生的出油量和花生的质量。 ( 成正比例关系 )
(3)用同样大的正方形地砖铺地,地砖的块数和铺地的面积。(成正比例关系 )
(4)一个商场每天的营业时间一定,每天接待顾客的数量与营业额。 (不成比例关系 )
(5)行驶的路程一定,车轮的周长与车轮需要转动的圈数。 (成反比例关系)
(6)一条公路,已经修了的米数与没有修的米数。 (不成比例关系 )
(7)梯形的面积一定,它的上下底的和与高。 ( 成反比例关系 )
(8)y=x (成正比例关系 )
四、一个啤酒厂生产情况记录表如下。(共20分)
工作时间(时)
1
2
3
4
5
6
工作总量(吨)
20
40
60
80
100
120
①写出几组工作总量与相对应的工作时间的比,并比较比值的大小。(4分)
……
②这个比值表示(工作效率)。(3分)
③工作总量与工作时间成正比例关系吗?为什么?(3分)
答:工作总量与工作时间成正比例关系,因为。
④在下图中把表中工作时间和工作总量所对应的点描出来,并按顺序把它们连接起来。再根据图象估计一下,3.5小时能生产啤酒( 70吨 );要生产150吨啤酒需要( 7.5 )小时。(10分)
载质量/t
2.5
4
5
6
8
10
数量/辆
48
30
24
20
15
12
五、运输公司要将一批物资运往某地。车辆载质量与所需车辆的数量如下表。(共12分)
①根据上表的信息,你能算出这批物资一共有多少吨吗?(3分)
2.5×48=120(吨)
答:这批物资一共有120吨。
②汽车载质量z表示,需要汽车的数量用s表示,这批物资的质量用N表示。用式子表示z、s、N之间的关系为( N=zs )。(3分)
③z和s成什么比例关系?为什么?(3分)
2.5×48=4×30=5×24=6×20=8×15=10×12
答:z和s成反比例关系,因为汽车载质量×需要汽车的数量=这批物资的质量(一定)。
④如果这批物资用载质量为7.5吨的汽车一次运完,需要(16)辆汽车来运。(3分)
120÷7.5=16(辆)
六年级 第7周 二级监测卷
监测内容:正比例和反比例
时间:40分钟 满分100分
一、填一填。(每空4分,共52分)
1.4A=5B(A、B均不为0),那么A和B成( 正 )比例关系。
2.下表中y和x两个量成正比例关系,请把表格填写完整。
x
4
12
18
48
20
36
y
2
6
9
24
10
18
3.想一想,填一填。
(1)物品的总价一定,它的单价和数量成(反)比例。 (2)每公顷的施肥量一定,施肥的公顷数和施肥总量成( 正 )比例。 (3)三角形的高一定,它的面积和底成(正)比例 (4)比的前项一定,后项和比值成( 反 )比例。
(5)甲数是乙数的80%,甲数和乙数成( 正 )比例。
(6)圆的面积和圆的半径的平方成( 正 )比例。
(7)100m往返跑,所需的时间与跑的速度成( 反 )比例。
二、选择。(将正确答案的序号填在括号里)(每题5分,共15分)
1.下列三个关系式中,x 与y(x.y均不为0)成正比例关系的是( C )。
A. x+y=10 B. C. x=10y
2.把60升水倒入一个圆柱形容器中,水的高度和容器内部的底面积( A?)。 A. 成反比例关系 B. 成正比例关系 C.不成比例关系
3.如右图,根据图估计一下,4.5小时可以生产( B )吨啤酒。
A. 70
B. 63
C. 72
D. 65
四、学校用一笔钱购买图书,下面是图书的单价及可购买图书数量的情况。(共18分)
单价/元
20
12
40
50
数量/本
300
500
150
120
(1)把上表填完整。(6分)
(2)在下图中先描出表示单价和相对应数量的点,再把它们按顺序连起来。(6分)
(3)根据图像可以知道,图书的单价与可购买图书数量成(反 )比例关系。
根据图像估计一下,当单价是25元时,可以购买图书(240)本。(6分)
如图表示某集团甲、乙两个车间加工零件数与时间的关系。(共15分)
(1)乙车间生产的零件数与时间成正比例吗?为什么?(4分)
答:乙车间生产的零件数与时间成正比例,因为。 (2)如果生产10万个零件,那么乙车间比甲车间少用几个月?(5分)
10÷(2÷1)=5(个) 10÷(4÷4)=10(个) 10-5=5(个)
答:乙车间比甲车间少用5个月。
(3)根据图像判断,乙车间5.5个月能生产多少个零件?这时比甲车间多生产多少个零件?(6分)
5.5×2=11(万个)
5.5×1=5.5(万个)
11-5.5=5.5(万个)
或5.5×(2-1)=5.5(万个)
答:乙车间5.5个月能生产11万个零件,这时比甲车间多生产5.5万个零件。
