【备战2020】高考数学二轮专题:立体几何 复习学案(上海地区专用)
文档属性
| 名称 | 【备战2020】高考数学二轮专题:立体几何 复习学案(上海地区专用) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-29 10:33:47 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
课题 立体几何 单元 第章 学科 数学 年级 十二
学习 目标 1.计算多面体及旋转体中二面角; 2.计算多面体及旋转体中的其他角与距离问题; 3.掌握立体几何中的综合应用问题的解决方法.
重点 1.多面体与旋转体中的二面角的计算方法; 2.多面体与旋转体中其他角与距离的计算方法; 3.立体几何综合应用.
难点 立体几何综合应用.
【备考2020】高考数学二轮专题复习学案
专题一 立体几何
教学安排
版块 时长
1 知识梳理 30
2 例题解析 60
3 巩固训练 20
4 师生总结 10
5 课后练习 30
一、线线、线面、面面关系
(一)、平面:平面及其表示方法;平面的基本性质。
1、 平面用平行四边形表示,常用表示方法:①一个大写字母,②一个小写希腊字母,③三个或者三个以上的字母;
2、三个公理;三个推论:
公理一:如果一条线上的两个点在平面上则该线在平面上
公理二:如果两个平面有一个公共点则它们有一条公共直线且所有的公共点都在这条直线上
公理三:三个不共线的点确定一个平面
推论一:直线及直线外一点确定一个平面
推论二:两相交直线确定一个平面
推论三:两平行直线确定一个平面
(二)、线线关系
1、两条直线的关系:
从面的角度,分为共面和不共面;
从交点的角度,分为相交,平行和异面。
公理4:平行于同一直线的两条直线相互平行。
推论:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补。
2、异面直线
(1)异面直线定义:不同在任何一个平面内的两条直线。
(2)异面直线画法:
(3)异面直线证法:反证法,即证明两直线既不平行也不相交。
(4)求异面直线所成的角
异面直线所成的角是指过空间任意一点O分别作两条异面直线的平行线,所得的两条相交直线所成的锐角(或直角)。它的取值范围为。
辨析:异面直线所成的角的取值范围是;向量所成的角的取值范围是。
所以,用向量方法求异面直线所成的角时,如果得出的是钝角,还要修正为锐角。
异面直线所成的角求法:
① 几何法:通过直线搬动,具体搬动一条直线还是两条都搬动,要看实际情况。
② 代数法:采用向量运算。
(三)、线面关系
直线与平面的位置关系是:直线在平面内、平行和相交。
1、直线在平面内:由公理1判断;
2、直线与平面平行:
判断一条直线与平面平行的方法:
①定义:直线与平面没有公共点;②在平面上找到一条直线与该直线平行
定理:一条直线与平面平行,经过这条直线作一个平面与已知平面相交,那么交线与这条直线平行。
3、直线与平面相交
(1)直线与平面的垂直:
① 定义:直线与平面内所有直线都垂直。
② 定理:直线与平面内两条相交直线垂直,那么直线垂直于平面。
(2)直线与平面的交角,分以下两种情况:
①直线和平面所成的角:直线与它在平面内的射影所成的锐角。
②直线与平面平行或在平面内,记为;直线与平面垂直,记为。
(四)、面面关系:平行和相交
1、两个面平行判断方法:
① 定义:两个平面没有交点;
② 定理:一个面上有两条相交直线与另一个面平行,则这两个平面互相平行。
性质:如果两个平面平行,作一平面与这两个面相交,则两条交线平行。
两个面相交:
(1)二面角定义
当两个平面相交时,它们的交线将各平平面面分割成两个半平面,由两个半平面及交线所组成的空间图形叫做二面角,记作。交线叫做二面角的棱,两个半平面叫做二面角的面(如图)
(2)二面角的度量
二面角的平面角:
在二面角的棱上任取一点,过分别在面和内作棱的垂线所成的角叫做二面角的平面角(如图)。用平面角的大小来表示二面角的大小。
范围:二面角的大小的范围
计算:关键在于作出二面角的平面角,通常作法有:
①定义法:从二面角的棱上一点分别在两个半平面内作垂直于棱的两条射线。在二面角的棱上选取点时要注意和已知条件的沟通。
②垂面法:过二面角内一点作垂直于棱的平面。该平面与二面角的两个半平面的交线所成的角就是所求的角。
(3)面面垂直:
①定义:若两个平面的二面角为直二面角,则这两个面互相垂直。
判定定理:一个平面过另一平面的垂线,则这两个平面相互垂直。
二、判定定理归纳(线线、线面、面面的平行和垂直判定)
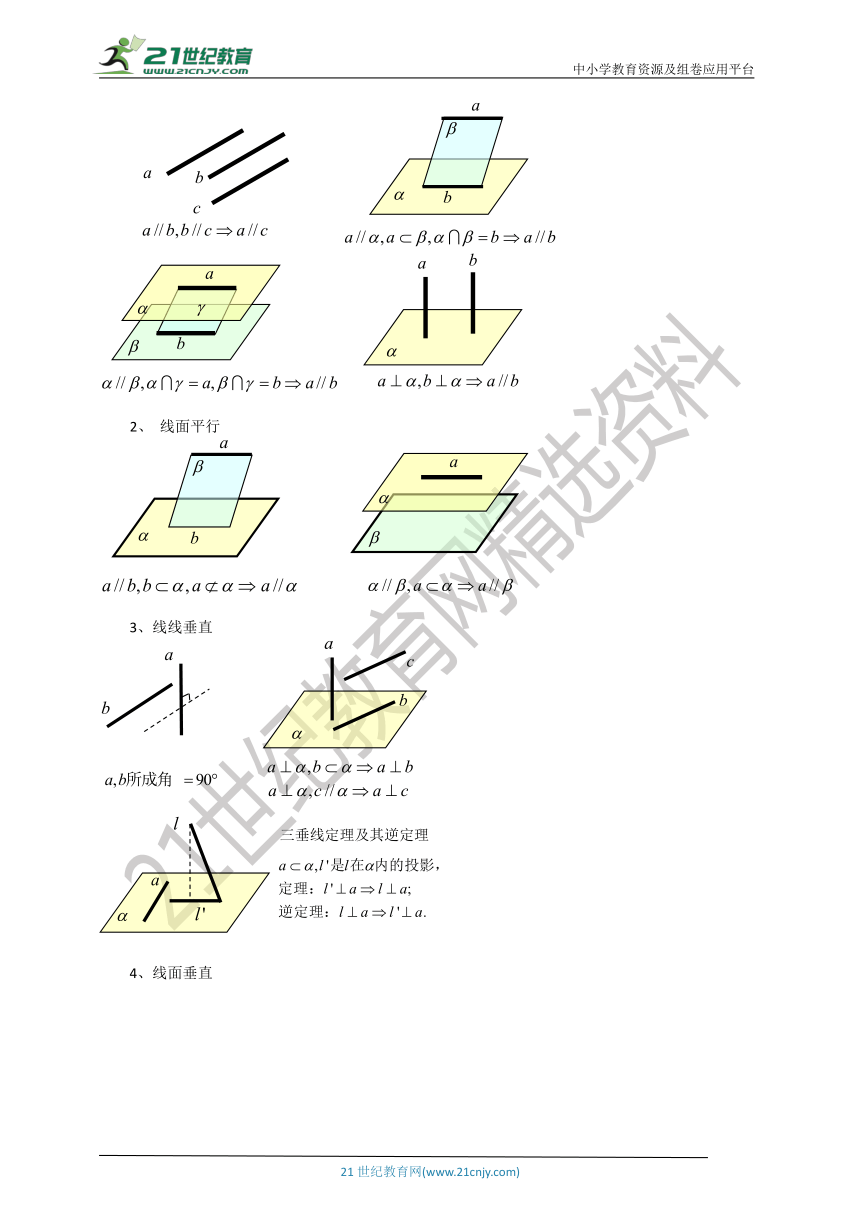
线线平行
线面平行
3、线线垂直
4、线面垂直
三、多面体与旋转体
(一)棱柱
1、由几个多边形围成的封闭的几何体叫做多面体。
2、两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的多面体叫做棱柱。棱柱的互相平行的两个面叫做棱柱的底面,其余各面叫做棱柱的侧面,相邻的两个侧面的公共边叫做棱柱的侧棱,两个底面间的距离叫做棱柱的高。
棱柱的基本性质:
棱柱的侧面都是平行四边形。
棱柱的两个底面及平行于底面的截面都是全等的多边形。
3、侧棱与底面不垂直的的棱柱叫做斜棱柱。侧棱与底面垂直的棱柱叫做直棱柱。底面是正多边形的直棱柱叫做正棱柱。
性质:
直棱柱侧面都是矩形。
直棱柱侧棱与高相等。
正棱柱的侧面都是全等的矩形。
4、底面是平行四边形的棱柱叫做平行六面体。底面是矩形的直棱柱是长方体。长方体的对角线平方等于三边长的平方和。
5、夹在两个平行平面间的两个几何体,如果被平行于这两个平面的任何平面所截得的两个截面的面积都相等,那么这两个几何体的体积相等。
6、.
(二)棱锥
1、有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。棱锥的这个多边形的面叫做底面,其余各个三角形的面叫做侧面。相邻的两个侧面的公共边叫做棱锥的侧棱。各个侧面的公共顶点叫做棱锥的顶点,顶点到底面的距离叫做棱锥的高。
棱锥的基本性质:
如果一个棱锥被平行于底面的一个平面所截,那么:
侧棱和高被这个平面分成比例线段;
截面和底面都是相似多边形;
截面面积与底面面积之比,等于顶点到截面与顶点到底面的距离平方之比。
2、如果一个棱锥的底面是正多边形,且顶点在底面的射影是底面的中心,这个棱锥叫做正棱锥。
正棱锥的性质:
各侧棱相等,各侧面都是全等的等腰三角形。
正棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形。
正棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。
3、各个面都是全等的等边三角形的三棱锥称为正四面体。
正多面体:
类型 面数 棱数 顶点数 每面边数 每顶点棱数
正4面体 4 6 4 3 3
正6面体 6 12 8 4 3
正8面体 8 12 6 3 4
正12面体 12 30 20 5 3
正20面体 20 30 12 3 5
4、
(三)圆柱、圆锥与球
将矩形ABCD(及其内部)绕其一条边AB所在直线旋转一周,所形成的几何体叫做圆柱,AB所在直线叫做圆柱的轴,线段AD和BC旋转而成的圆面叫做圆柱的底面,线段CD旋转而成的曲面叫做圆柱的侧面,CD叫做圆柱侧面的一条母线,圆柱的两个底面间的距离(即AB得长度)叫做圆柱的高。
,,
将直角三角形ABC(及其内部)绕其一条直角边AB所在直线旋转一周,所形成的几何体叫做圆锥,AB所在直线叫做圆锥的轴,点A叫做圆锥的顶点,直角边BC旋转而成的圆面叫做圆锥的底面,斜边AC旋转而成的曲面叫做圆锥的侧面,斜边AC叫做圆锥侧面的一条母线,圆锥的顶点到底面间的距离(即AB的长度)叫做圆锥的高。
,,
将圆心为O的半圆(及其内部)绕起直径AB所在的直线旋转一周,所形成的几何体叫做球,半圆的圆弧所形成的曲面叫做球面,易知,点O到球面上任意点的距离都相等,把点O称为球心,把原半圆的半径和直径分别称为球的半径和球的直径。
平面上的两点之间线段最短,该线段的长度就是两点之间的距离,类似地,要定义球面上两点之间的距离,也应该在球面上找到联结两点的最短路径,该路径的长度就是球面上亮点之间的距离。可以证明,在联结球面上亮点的路径中,通过该两点的大圆劣弧最短,因此该弧的长度就是这两点的球面距离。
EMBED Equation.DSMT4 ,
四、空间向量
1、会用向量的方法求线与线、线与面、面与面所成的角,点与点、点与面之间的距离。
提示:立体几何的计算主要是求角和距离,侧重求角。
计算方法:
① 线与线所成角:设分别与直线平行的向量为,则,则直线所成角为(注意:两直线所成角的范围是)。
② 线与面所成角:设与直线平行的向量为,平面的法向量为,则,则直线与平面所成角为(注意:线与面所成角的范围是)。
③二面角求法:设平面的法向量为,且,则二面角大小为或(注意:二面角的范围是)。
④ 点到点的距离:若已知向量,则点A、B的距离为。
⑤ 点到面的距离:已知点A是平面外的点,点B是内的点,且的法向量为,则点A到平面的距离为。
2、基础命题:
(1)两条直线平行或重合的充要条件是它们的方向向量互相平行;
(2)一条直线与一个平面平行或在一个平面内的充要条件是这条直线的方向向量垂直于该平面的法向量;
(3)两个平面平行或重合的充要条件是它们的法向量互相平行。
五、三视图
1.三视图:三视图是观测者从三个不同位置观察同一个空间几何体而画出的图形.
视图:将人的视线规定为平行投影线,然后正对着物体看过去,将所见物体的轮廓用
正投影法绘制出来该图形称为视图.
结论:正俯一样长,俯侧一样宽,正侧一样高.
2.常用的三视图
(1)常见旋转体的三视图
(2)常见多面体的三视图原则
常用原则就是在绘制三视图时,务必做到正视图、侧视图高平齐,正视图、俯视图长对正,俯视图、侧视图宽相等.具体在安排方法时,正视图与侧视图在同一水平位置,且正视图在左,侧视图在右,俯视图在正视图的正下方.具体图形如下:
1、长方体
2、圆锥
3、圆柱
4、四棱锥
5、三棱锥
一、线线角、线面角、二面角的计算与证明
1、几何法
例1(长宁嘉定金山区2020届高三上期末(一模))如图,底面为矩形的直棱柱满足:,,.
(1)求直线与平面所成的角的大小;
(2)设、分别为棱、上的动点,
求证:三棱锥的体积为定值,并求出该值.
解析:(1)由直棱柱知,所以
又因为,所以直线平面, ……………2分
所以即直线与平面的所成角 ……………4分
由题意,,所以
所以直线与平面的所成角. ……………6分
(2)记点到平面的距离为,三角形的面积为,则
, ………………3分
由已知,, ………………6分
所以为定值. ………………8分
例2.(2019·上海交大附中高三月考)设三棱锥的底面是正三角形,侧棱长均相等,是棱上的点(不含端点),记直线与直线所成的角为,直线与平面所成的角为,二面角的平面角为,则三个角、、中最小的角是______.
【答案】
【解析】
作交于,由于,,所以为正三棱锥,由对称性知.取中点,连接,作平面,交平面于,连接.作平面,交平面于,连接.作,交于,连接,所以.由于,所以.由于平面,所以.由于,平面,所以.
.因为,在上,平面于,平面于,所以.所以.所以.由于都是锐角,所以.
由于在上,由对称性,而,则,由于也是锐角,所以.
综上所述,三个角中的最小角是.
故答案为:.
【巩固训练】
1.(2019·上海高三)如图,在过正方体的任意两个顶点的所有直线中,与直线异面的直线的条数为______.
【答案】12
【解析】
由题中正方体可得与异面的直线有:,,,,,;,,,,,,共12条.
故答案为12
2.((奉贤区2020届高三上期末(一模))已知长方体中,,,,点是棱上的动点.
(1)求三棱锥的体积;
(2)当点是棱上的中点时,求直线与
平面所成的角(结果用反三角函数值表示).
解析:(1)因为长方体中有平面
因为与平行,所以点到线段的距离等于
所以 -----------3分
所以 -----------7分
(2)
长方体中
可得,,
从而 -----------3分
过点作平面
由得
求得 -----------2分
由平面,且
知为直线与平面所成的角 -----------1分
中,
所以
所以直线与平面所成的角的大小为 -----------1分
3.(2019·上海曹杨二中高二期末)已知正四棱锥的棱长都相等,侧棱、的中点分别为、,则截面与底面所成的二面角的余弦值是________.
【答案】
【解析】
如图,
正四棱锥P﹣ABCD中,O为正方形ABCD的两对角线的交点,则PO⊥面ABCD,PO交MN于E,则PE=EO,
又BD⊥AC,∴BD⊥面PAC,
过A作直线l∥BD,则l⊥EA,l⊥AO,
∴∠EAO为所求二面角的平面角.
又EO=AO=a,AO=a,∴AE=a
∴cos∠EAO=.
∴截面AMN与底面ABCD所成的二面角的余弦值是.
2、向量法
(2019·上海高三)我国古代数学名著《九章算术》中记载了有关特殊几何体的定义:阳马指底面为矩形,一侧棱垂直于底面的四棱锥,堑堵指底面是直角三角形,且侧棱垂直于底面的三棱柱.
(1)某堑堵的三视图,如图1,网格中的每个小正方形的边长为1,求该堑堵的体积;
(2)在堑堵中,如图2,,若,当阳马的体积最大时,求二面角的大小.
【解析】
(1)由三视图还原原几何体如图,
可知该几何体为直三棱柱,底面是等腰直角三角形,直角边长为,
直三棱柱的高为2,
则其体积为V;
(2)∵A1A=AB=2,阳马B﹣A1ACC1的体积:
VA1A×AC×BCAC×BC(AC2+BC2)AB2,
当且仅当AC=BC时,,
以C为原点,CB为x轴,CA为y轴,CC1为z轴,建立空间直角坐标系,
则A1(0,,2),B(,0,0),C1(0,0,2),
∴(0,,2),(,0,0),(0,,0),(,0,﹣2),
设平面CA1B的法向量(x,y,z),
则,取y,得(0,,﹣1),
设平面C1A1B的法向量(a,b,c),
则,取a,得(,0,1),
设当阳马B﹣A1ACC1体积最大时,二面角C﹣A1B﹣C1的平面角为θ,
则cosθ,
∴当阳马B﹣A1ACC1体积最大时,二面角C﹣A1B﹣C1的大小为arccos.
例2(2019·上海高三月考)直三棱柱中,底面为等腰直角三角形,且,,,是侧棱上一点,设.
(1)若,求证:;
(2)若多面体的体积为,求直线与平面所成的角.
【解析】
证明:以为坐标原点,以射线分别为、、 轴,建立空间直角坐标系如图所示:
则,,,,
所以,,
所以,
所以.
因为三棱锥的体积为
,
三棱柱的体积为
,
又因为,
所以,解得,即为的中点.
因为平面,
所以即为直线与平面所成的角.
在中,,
所以为等腰直角三角形,
故即为所求的角.
【巩固训练】
1(2019·上海复旦附中期末)在长方体中,,,则异面直线与所成角的余弦值为
A. B. C. D.
【答案】C
【解析】
以D为坐标原点,DA,DC,DD1为x,y,z轴建立空间直角坐标系,则,所以,
因为,所以异面直线与所成角的余弦值为,选C.
2.(2019·上海市洋泾中学高三月考)如图,在直三棱柱中,已知,.
(1)求四棱锥的体积;
(2)求二面角的大小.
【解析】
(1)因为,三棱柱是直三棱柱,所以,从而是四棱锥的高
四棱锥的体积为
(2)如图建立空间直角坐标系
则,,,,
设AC的中点为M,,,平面,即是平面的一个法向量
设平面的一个法向量是,,
令,解得,
设法向量与的夹角为,二面角的大小为,显然为锐角
,
二面角的大小为
三视图
例1.(2019·上海市育才中学高三)正方体中, 为棱的中点(如图)用过点的平面截去该正方体的上半部分,则剩余几何体的左视图为( )
A. B.
C. D.
【答案】D
【解析】
由题意可知:过点、、的平面截去该正方体的上半部分,如图直观图,则几何体的左视图为D,故选D.
【巩固训练】
1.(2019·上海市七宝中学高三月考)如图,直三棱柱的主视图是边长为2的正方形,且俯视图为一个等边三角形,则该三棱柱的左视图面积为___________.
【答案】
【解析】
由三视图得到三棱柱的侧视图为以底面正三角形的高为一边,以棱柱高为另一边的矩形,
所以侧视图的面积为,故答案为 .
三、距离与表面积、体积的计算
1、几何法
例1.(2019·上海交大附中高三月考)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( )
A. B. C. D.
【答案】D
【解析】
解法一:为边长为2的等边三角形,为正三棱锥,
,又,分别为、中点,
,,又,平面,平面,,为正方体一部分,,即 ,故选D.
解法二:
设,分别为中点,
,且,为边长为2的等边三角形,
又
中余弦定理,作于,,
为中点,,,
,,又,两两垂直,,,,故选D.
例2.(2018·上海市南洋模范中学高二期中)在封闭的直三棱柱内有一个体积为的球.若,,则的最大值是( )
A. B.
C. D.
【答案】B
【解析】要使球的体积最大,必须球的半径最大.由题意,知当球与直三棱柱的上、下底面都相切时,球的半径取得最大值,为,此时球的体积为,故选.
例3(2019·上海高三)已知直三棱柱的6个顶点都在球O的球面上,若,,,,则球的表面积为______.
【答案】
【解析】由题意,直三棱柱的底面为直角三角形,
可把直三棱柱的补成一个长方体,
则直三棱柱的外接球和长方体的外接球是同一个球,
又由长方体的对角线长等于球的直径,且,
即,即,
所以球的表面积为.
故答案为:
例4(2019·上海市复兴高级中学高三)如图,长方体的边长 , ,它的外接球是球,则,这两点的球面距离等于_________.
【答案】
【解析】
由题意,,所以,
所以.
【巩固训练】
1.(2019·上海高三期末)魏晋时期数学家刘徽在他的著作九章算术注中,称一个正方体内两个互相垂直的内切圆柱所围成的几何体为“牟合方盖”,刘徽通过计算得知正方体的内切球的体积与“牟合方盖”的体积之比应为:若正方体的棱长为2,则“牟合方盖”的体积为
A.16 B. C. D.
【答案】C
【解析】正方体的棱长为2,则其内切球的半径,
正方体的内切球的体积,
又由已知,.
故选C.
2、向量法
例1(2019·上海高三)在四棱锥中,设向量,,,则顶点到底面的距离为_________
【答案】2
【解析】
设平面的法向量
则,令,则,
点到底面的距离:
本题正确结果:
一、空间距离:
空间距离主要有①点和平面的距离;②直线与平面的距离;③平面与平面的距离.
空间距离的求法①定义法:通过找辅助平面,通过作图-证明-计算求解.
②转化法:注意各种距离之间的相互转化.
③等体积法:间接求距离的方法,也是常用方法.
球面距离的求法①定义法:通过球面上两点大圆劣弧的长度为这两点的球面距离.
二、空间角:
空间角主要有:①异面直线所成的角;②直线与平面所成的角.
1.异面直线所成的角其范围是,主要求法有:
①平移法:利用三角形中位线、平行四边行对边平行,相似三角形进行平移,再解三角形.
②向量法:异面直线与的夹角为,则.
2.直线和平面所成角其范围是,主要求法有:
①定义法:求斜线与其射影的夹角.
②向量法:直线 与平面所成角,:(为的法向 量,为与的交点,为上不同于的任意一点).
3.二面角其范围是,主要求法有:
①定义法:适用于对称的二面角,过棱上一点分别在两个半平面引垂线.
②三垂线法:当题中易得一个面内一点到另一个面的垂线时,可使用三垂线定理或逆定理作出二面角的平面角.
③面积射影法:,它可以回避作出二面角的平面角,尤其是对解答“无棱”二面角问题更为适用.
④垂面法:过棱上一点的棱的垂面,垂面与两个半平面的交线所夹角即为二面角的平面角.
⑤向量法:求二面角,(,分别为两个平面的法向量).
一、单选题
1.(2019·上海高三月考)设,是两条不同的直线,是一个平面,则下列命题正确的是 ( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
【答案】B
【解析】,,则可能平行,错;
,,由线面平行的性质可得,正确;
,,则, 与异面;错,
,,与可能平行、相交、异面,错,.故选B.
2.(2019·上海交大附中高三月考)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为
A. B. C. D.
【答案】D
【解析】
解法一:为边长为2的等边三角形,为正三棱锥,
,又,分别为、中点,
,,又,平面,平面,,为正方体一部分,,即 ,故选D.
解法二:
设,分别为中点,
,且,为边长为2的等边三角形,
又
中余弦定理,作于,,
为中点,,,
,,又,两两垂直,,,,故选D.
3.(2019·上海高三期末)已知正方体,点是棱的中点,设直线为,直线为.对于下列两个命题:①过点有且只有一条直线与、都相交;②过点有且只有一条直线与、都成角.以下判断正确的是( )
A.①为真命题,②为真命题 B.①为真命题,②为假命题
C.①为假命题,②为真命题 D.①为假命题,②为假命题
【答案】B
【解析】
解:直线AB与A1D1 是两条互相垂直的异面直线,点P不在这两异面直线中的任何一条上,如图所示:
取BB1的中点Q,则PQ∥A1D1,且 PQ=A1D1,设A1Q与AB交于E,则点A1、D1、Q、E、P共面,
直线EP必与A1D1 相交于某点F,则过P点有且只有一条直线EF与a、b都相交,故①为真命题;
分别平移a,b,使a与b均经过P,则有两条互相垂直的直线与a,b都成45°角,故②为假命题.
∴①为真命题,②为假命题.
故选:B.
4.(2019·上海市复兴高级中学期末)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
A. B.
C. D.
【答案】A
【解析】
对于B项,如图所示,连接CD,因为AB∥CD,M,Q分别是所在棱的中点,所以MQ∥CD,所以AB∥MQ,又AB?平面MNQ,MQ?平面MNQ,所以AB∥平面MNQ,
同理可证,C,D项中均有AB∥平面MNQ.
故选:A.
5.(2019·上海复旦附中期末)在长方体中,,,则异面直线与所成角的余弦值为
A. B. C. D.
【答案】C
【解析】
以D为坐标原点,DA,DC,DD1为x,y,z轴建立空间直角坐标系,则,所以,
因为,所以异面直线与所成角的余弦值为,选C.
6.(2019·上海市建平中学高三考试)如图,在直三棱柱中,,,已知G与E分别为和的中点,D和F分别为线段AC和AB上的动点(不包括端点),若,则线段DF的长度的平方取值范围为( ).
A. B. C. D.
【答案】D
【解析】建立如图所示的空间直角坐标系,则A(0,0,0),E(0,1,),
G( ,0,1),F(x,0,0),D(0,y,0)
∴∵GD⊥EF,
∴x+2y﹣1=0,∴x=1﹣2y
DF
∵0<y<1∴当y时,线段DF长度的最小值是
又y=0时,线段DF长度的最大值是1
而不包括端点,故y=1不能取;
故线段DF的长度的取值范围是:[,1).
即线段的长度的平方取值范围为,
故选:D.
7.(2019·上海格致中学高三)如图,已知三棱锥,平面,是棱上的动点,记与平面所成的角为,与直线所成的角为,则与的大小关系为( )
A. B.
C. D.不能确定
【答案】C
【解析】如图所示:∵PA⊥平面ABC,∴PD与平面ABC所成的角=∠PDA,
过点A作AE⊥BC,垂足为E,连接PE,
∵PA⊥平面ABC,∴PA⊥BC,∴BC⊥平面PAE,∴BC⊥PE,
在Rt△AED,Rt△PAD,Rt△PED中:cos,cos,cos,
∴cos cos cos< cos,又均为锐角, ∴,故选C.
8.(2019·上海华师大二附中高三)我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.“开立圆术”相当于给出了已知球的体积,求其直径的一个近似公式,人们还用过一些类似的近似公式,根据判断,下列近似公式中最精确的一个是( )
A. B. C. D.
【答案】B
【解析】
由球体的体积公式得,,,
,,,与最为接近,故选C.
9.(2020·上海市金山中学月考)如图所示,正方体的棱长为1,过点作平面的垂线,垂足为,则以下说法中错误的是( )
A.点是的垂心
B.垂直于平面
C.的延长线经过点
D.直线和所成角为
【答案】D
【解析】为等边三角形,,
到各顶点的距离相等,∴A正确.
,
∴平面平面,平面,∴B正确.
连接,则,
又,平面,
三点共线,∴C正确.
由C选项可知,直线和所成角即是直线和所成角,
在中,易得,
所以直线和所成角不是,因此D错.
故选D.
10(2020·上海高三)在直三棱柱中,,,.
(1)求异面直线与所成角的大小;
(2)求直线与平面的距离.
【解析】
(1)因为,所以 (或其补角)是异直线与所成角.
因为,,,
所以平面,所以.
中,,所以,
所以异面直线与所成角的大小为.
(2)因为平面,所以到平面的距离等于到平面的距离,
设到平面的距离为,因为,
,可得,
直线与平面的距离为.
11.(2019·上海市七宝中学高三期末)在长方体ABCD-A1B1C1D1中(如图),AD=AA1=1,AB=2,点E是棱AB的中点.
(1)求异面直线AD1与EC所成角的大小;
(2)《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,试问四面体D1CDE是否为鳖臑?并说明理由.
解:(1)取CD中点F,连接AF,则AF∥EC,
∴∠D1AF为异面直线AD1与EC所成角.
在长方体ABCD-A1B1C1D1中,由AD=AA1=1,AB=2,
得
∴△AD1F为等边三角形,则.
∴异面直线AD1与EC所成角的大小为;
(2)连接DE,∵E为AB的中点,∴DE=EC=,
又CD=2,∴DE2+CE2=DC2,得DE⊥CE.
∵D1D⊥底面DEC,则D1D⊥CE,∴CE⊥平面D1DE,得D1E⊥CE.
∴四面体D1CDE的四个面都是直角三角形,
故四面体D1CDE是鳖臑.
12.(2019·上海交大附中高三期末)如图所示,三棱柱的侧面是圆柱的轴截面,C是圆柱底面圆周上不与A、B重合的一个点.
(1)若圆柱的轴截面是正方形,当点C是弧AB的中点时,求异面直线与AB的所成角的大小(结果用反三角函数值表示);
(2)当点C是弧AB的中点时,求四棱锥体积与圆柱体积的比.
解:
(1) 连接,由,可得即为异面直线与的所成的角或补角,不妨设,则,在△中,由余弦定理知,,故异面直线与的所成角的大小为 .
(2) 由为直径,可得,又平面,所以,又,所以平面,故四棱锥体积,圆柱的体积为,又,所以四棱锥体积与圆柱体积的比为.
13.(2019·上海高三期末)如图,在正六棱锥中,已知底边为2,侧棱与底面所成角为.
(1)求该六棱锥的体积;
(2)求证:
【解析】
∵在正六棱锥P﹣ABCDEF中,底边长为2,侧棱与底面所成角为60°.
连结AD,过P作PO⊥底面ABCD,交AD于点O,
则AO=DO=2,∠PAO=60°,∴PA=2AO=4,
PO2,
SABCDEF=6×()=6,
∴该六棱锥的体积V12.
(2)连结CE,交AD于点O,连结PG,
∵DE=CD,AE=AD,∴AD⊥CE,O是CE中点,
∵PA=PC,∴PG⊥CE,
∵PG∩AD=G,∴CE⊥平面PAD,
∵PA?平面PAD,∴PA⊥CE.
14.(2019·上海高三月考)直三棱柱中,底面为等腰直角三角形,且,,,是侧棱上一点,设.
(1)若,求证:;
(2)若多面体的体积为,求直线与平面所成的角.
【解析】
证明:以为坐标原点,以射线分别为、、 轴,建立空间直角坐标系如图所示:
则,,,,
所以,,
所以,
所以.
因为三棱锥的体积为
,
三棱柱的体积为
,
又因为,
所以,解得,即为的中点.
因为平面,
所以即为直线与平面所成的角.
在中,,
所以为等腰直角三角形,
故即为所求的角.
知识梳理
A
B
A
B
O
M
N
(1)从前面向后面投射所得的视图称主视图—能反映物体的前面形状;
(2)从上面向下面投射所得的视图称俯视图—能反映物体的上面形状;
(3)从左面向右面投射所得的视图称左视图—能反映物体的左面形状.
三视图就是主视图、俯视图、左视图的总称.
1.圆柱的正视图和侧视图都是矩形,俯视图是圆;
2.圆锥的正视图和侧视图都是等腰三角形,俯视图是圆和圆心;
3.球的三视图都是圆.;
·
例题解析
反思总结
课后练习
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
