第二十二章二次函数专题复习—平行四边形的存在性问题课件(共20张PPT)
文档属性
| 名称 | 第二十二章二次函数专题复习—平行四边形的存在性问题课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1000.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-29 23:03:54 | ||
图片预览






文档简介
(共20张PPT)
二次函数专题复习
——平行四边形的存在性问题
1、二次函数一般式
一、二次函数式
2、二次函数顶点式
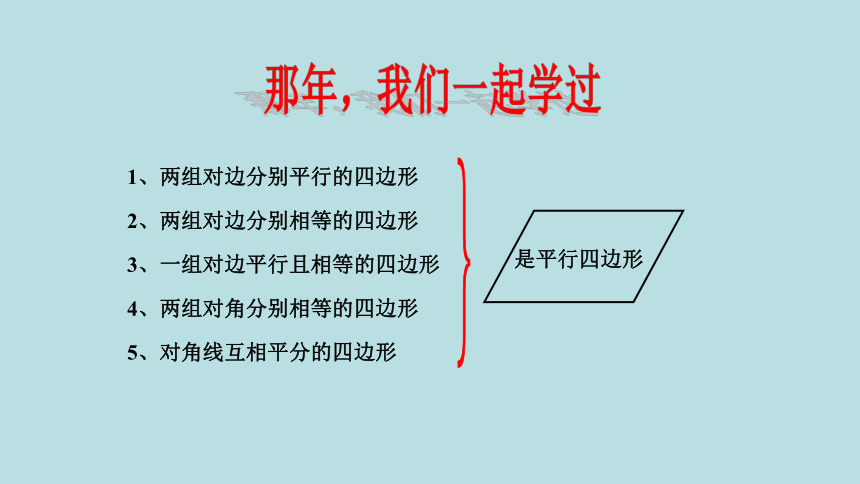
1、两组对边分别平行的四边形
2、两组对边分别相等的四边形
3、一组对边平行且相等的四边形
4、两组对角分别相等的四边形
5、对角线互相平分的四边形
是平行四边形
二次函数问题中平行四边形的存在性问题
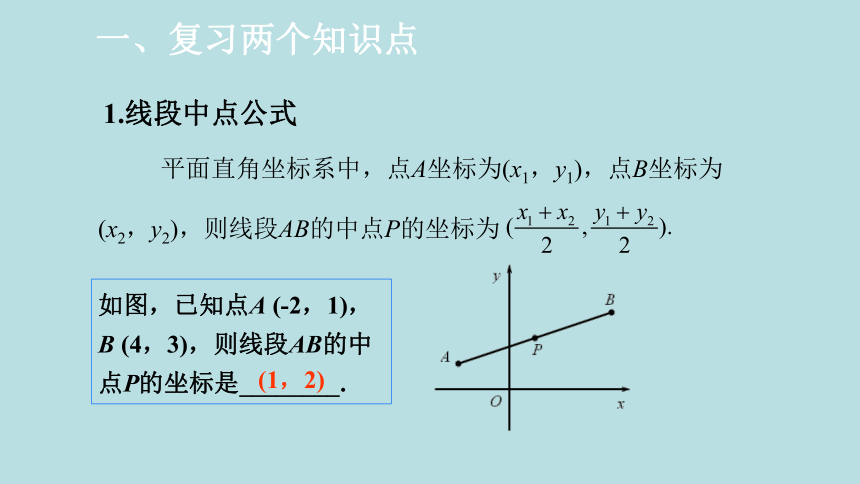
1.线段中点公式
一、复习两个知识点
平面直角坐标系中,点A坐标为(x1,y1),点B坐标为
(x2,y2),则线段AB的中点P的坐标为
如图,已知点A (-2,1),B (4,3),则线段AB的中点P的坐标是________.
(1,2)
2.线段的平移
一、复习两个知识点
平面内,线段AB平移得到线段A'B' ,则
①AB∥A'B' ,AB=A'B' ;②AA'∥BB',AA'= BB'.
如图,线段AB平移得到线段A'B' ,已知点A (-2,2),B (-3,-1), B' (3,1),则点A'的坐标是________.
(4,4)
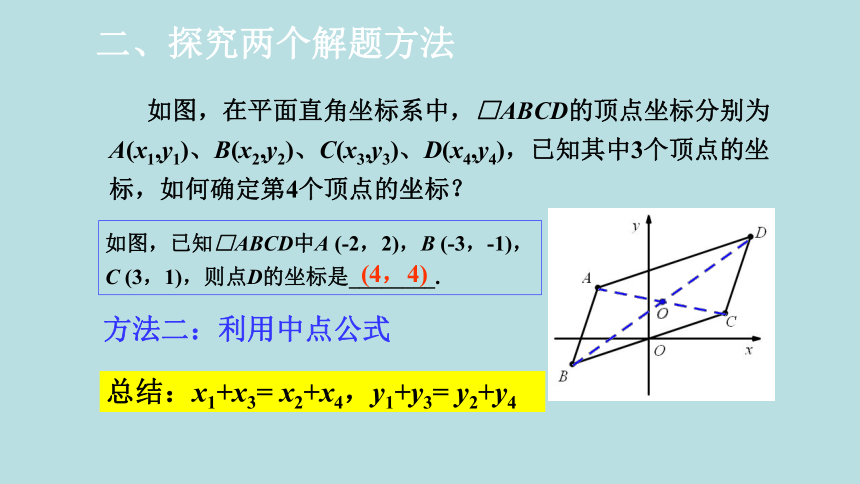
二、探究两个解题方法
如图,在平面直角坐标系中,□ABCD的顶点坐标分别为A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),已知其中3个顶点的坐标,如何确定第4个顶点的坐标?
如图,已知□ABCD中A (-2,2),B (-3,-1), C (3,1),则点D的坐标是________.
(4,4)
总结:x1-x2= x4-x3,y1-y2= y4-y3
或者 x4-x1= x3-x2,y4-y1= y3-y2 等
方法一:利用线段平移
二、探究两个解题方法
如图,在平面直角坐标系中,□ABCD的顶点坐标分别为A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),已知其中3个顶点的坐标,如何确定第4个顶点的坐标?
如图,已知□ABCD中A (-2,2),B (-3,-1), C (3,1),则点D的坐标是________.
(4,4)
总结:x1+x3= x2+x4,y1+y3= y2+y4
方法二:利用中点公式
二、探究两个解题方法
如图,在平面直角坐标系中,□ABCD的顶点坐标分别为A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),已知其中3个顶点的坐标,如何确定第4个顶点的坐标?
总结:x1+x3= x2+x4,y1+y3= y2+y4
方法二:中点公式法
方法一:平移法
总结: x1-x2= x4-x3,y1-y2= y4-y3等
三、一招制胜法
如图,在平面直角坐标系中,□ABCD的顶点坐标分别为A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),则4个顶点坐标之间的关系是什么?
即平行四边形中,两组相对顶点的横坐标之和相等,纵坐标之和也相等.
四、解决两类问题
例1 如图,平面直角坐标中,已知中A (-1,0),B (1,-2), C (3,1),点D是平面内一动点,若以点A 、B 、 C、 D为顶点的四边形是平行四边形,则点D的坐标是_________________________________.
(1,3), (-3,-3), (5,-1)
方法二:
中点法 x1+x3= x2+x4,y1+y3= y2+y4
方法一:
平移法 x1-x2= x4-x3,y1-y2= y4-y3
四、解决两类问题
例1 如图,平面直角坐标中,已知中A (-1,0),B (1,-2), C (3,1),点D是平面内一动点,若以点A 、B 、 C、 D为顶点的四边形是平行四边形,则点D的坐标是_________________________________.
(1,3), (-3,-3), (5,-1)
总结:三定一动问题,可以通过构造中点三角形得以解决.
说明:若题中四边形ABCD是平行四边形,
则点D的坐标只有一个结果__________.
四、解决两类问题
例2 已知,抛物线y=-x2+x+2 与x轴的交点为A、B,与x轴的交点为C,点M是平面内一点,判断有几个位置能使以点M、A、B、C为顶点的四边形是平行四边形,请写出相应的坐标.
先求出A(-1,0),B (2,0),C(0,2)
M1(3,2), M2 (-3,2),M3 (1,-2)
四、解决两类问题
例3 已知抛物线y=x2-2x+a(a<0)与y轴相交于点A,顶点为M. 直线y= 0.5x-a与y轴相交于点C,并且与直线AM相交于点N.
若点P是抛物线上一动点,求出使得以P、A、C、N为顶点的四边形是平行四边形的点P的坐标.
四、解决两类问题
例4 如图,平面直角坐标中,y=0.5x2+x-4与y轴相交于点B (0,-4),点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,写出相应的点Q的坐标.
设P(m, 0.5m2+m-4),Q (a, -a).
例5 如图,平面直角坐标中,y=x2-2x-3与x轴相交于点A (-1,0),点C的坐标是(2,-3),点P抛物线上的动点,点Q是x轴上的动点,判断有几个位置能使以点A、C、P、Q为顶点的四边形为平行四边形,写出相应的点Q的坐标.
设P(m, m2-2m-3),Q (a, 0).
四、解决两类问题
*
例6 如图,平面直角坐标中,y=-0.25x2+x与x轴相交于点B (4,0),点C在抛物线的对称轴上,点D在抛物线上,且以点O、B、C、D为顶点的四边形是平行四边形,写出相应的点D的坐标.
设C(m, 0.5m2+m-4),Q (a, 0).
四、解决两类问题
归纳与总结
二次函数问题中平行四边形的存在性问题,无论是“三定一动”,还是“两定两动”,一招制胜的方法,就是“中点法”,往往需要分三种情况,得出三个方程组求解。
祝福您!数学老师!
每当站在毕业班的讲台,总有做不完的题目,忙不完的事!
就连今天的研讨会,也需要匆匆的来,匆匆的去,学生等你看自习。
无论多忙,别忘了数学是需要思考的学科,但愿今天的“一招制胜法”能帮不您解决一些烦恼。
再忙也要注意身体,再委屈也要学会调节自己。
在这个充满任性的年代,面对名利,你来也好,不来也好,我就在这里,我们需要平和的心里。
身体健康!工作顺利!万事如意!中考大吉!
二次函数专题复习
——平行四边形的存在性问题
1、二次函数一般式
一、二次函数式
2、二次函数顶点式
1、两组对边分别平行的四边形
2、两组对边分别相等的四边形
3、一组对边平行且相等的四边形
4、两组对角分别相等的四边形
5、对角线互相平分的四边形
是平行四边形
二次函数问题中平行四边形的存在性问题
1.线段中点公式
一、复习两个知识点
平面直角坐标系中,点A坐标为(x1,y1),点B坐标为
(x2,y2),则线段AB的中点P的坐标为
如图,已知点A (-2,1),B (4,3),则线段AB的中点P的坐标是________.
(1,2)
2.线段的平移
一、复习两个知识点
平面内,线段AB平移得到线段A'B' ,则
①AB∥A'B' ,AB=A'B' ;②AA'∥BB',AA'= BB'.
如图,线段AB平移得到线段A'B' ,已知点A (-2,2),B (-3,-1), B' (3,1),则点A'的坐标是________.
(4,4)
二、探究两个解题方法
如图,在平面直角坐标系中,□ABCD的顶点坐标分别为A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),已知其中3个顶点的坐标,如何确定第4个顶点的坐标?
如图,已知□ABCD中A (-2,2),B (-3,-1), C (3,1),则点D的坐标是________.
(4,4)
总结:x1-x2= x4-x3,y1-y2= y4-y3
或者 x4-x1= x3-x2,y4-y1= y3-y2 等
方法一:利用线段平移
二、探究两个解题方法
如图,在平面直角坐标系中,□ABCD的顶点坐标分别为A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),已知其中3个顶点的坐标,如何确定第4个顶点的坐标?
如图,已知□ABCD中A (-2,2),B (-3,-1), C (3,1),则点D的坐标是________.
(4,4)
总结:x1+x3= x2+x4,y1+y3= y2+y4
方法二:利用中点公式
二、探究两个解题方法
如图,在平面直角坐标系中,□ABCD的顶点坐标分别为A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),已知其中3个顶点的坐标,如何确定第4个顶点的坐标?
总结:x1+x3= x2+x4,y1+y3= y2+y4
方法二:中点公式法
方法一:平移法
总结: x1-x2= x4-x3,y1-y2= y4-y3等
三、一招制胜法
如图,在平面直角坐标系中,□ABCD的顶点坐标分别为A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),则4个顶点坐标之间的关系是什么?
即平行四边形中,两组相对顶点的横坐标之和相等,纵坐标之和也相等.
四、解决两类问题
例1 如图,平面直角坐标中,已知中A (-1,0),B (1,-2), C (3,1),点D是平面内一动点,若以点A 、B 、 C、 D为顶点的四边形是平行四边形,则点D的坐标是_________________________________.
(1,3), (-3,-3), (5,-1)
方法二:
中点法 x1+x3= x2+x4,y1+y3= y2+y4
方法一:
平移法 x1-x2= x4-x3,y1-y2= y4-y3
四、解决两类问题
例1 如图,平面直角坐标中,已知中A (-1,0),B (1,-2), C (3,1),点D是平面内一动点,若以点A 、B 、 C、 D为顶点的四边形是平行四边形,则点D的坐标是_________________________________.
(1,3), (-3,-3), (5,-1)
总结:三定一动问题,可以通过构造中点三角形得以解决.
说明:若题中四边形ABCD是平行四边形,
则点D的坐标只有一个结果__________.
四、解决两类问题
例2 已知,抛物线y=-x2+x+2 与x轴的交点为A、B,与x轴的交点为C,点M是平面内一点,判断有几个位置能使以点M、A、B、C为顶点的四边形是平行四边形,请写出相应的坐标.
先求出A(-1,0),B (2,0),C(0,2)
M1(3,2), M2 (-3,2),M3 (1,-2)
四、解决两类问题
例3 已知抛物线y=x2-2x+a(a<0)与y轴相交于点A,顶点为M. 直线y= 0.5x-a与y轴相交于点C,并且与直线AM相交于点N.
若点P是抛物线上一动点,求出使得以P、A、C、N为顶点的四边形是平行四边形的点P的坐标.
四、解决两类问题
例4 如图,平面直角坐标中,y=0.5x2+x-4与y轴相交于点B (0,-4),点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,写出相应的点Q的坐标.
设P(m, 0.5m2+m-4),Q (a, -a).
例5 如图,平面直角坐标中,y=x2-2x-3与x轴相交于点A (-1,0),点C的坐标是(2,-3),点P抛物线上的动点,点Q是x轴上的动点,判断有几个位置能使以点A、C、P、Q为顶点的四边形为平行四边形,写出相应的点Q的坐标.
设P(m, m2-2m-3),Q (a, 0).
四、解决两类问题
*
例6 如图,平面直角坐标中,y=-0.25x2+x与x轴相交于点B (4,0),点C在抛物线的对称轴上,点D在抛物线上,且以点O、B、C、D为顶点的四边形是平行四边形,写出相应的点D的坐标.
设C(m, 0.5m2+m-4),Q (a, 0).
四、解决两类问题
归纳与总结
二次函数问题中平行四边形的存在性问题,无论是“三定一动”,还是“两定两动”,一招制胜的方法,就是“中点法”,往往需要分三种情况,得出三个方程组求解。
祝福您!数学老师!
每当站在毕业班的讲台,总有做不完的题目,忙不完的事!
就连今天的研讨会,也需要匆匆的来,匆匆的去,学生等你看自习。
无论多忙,别忘了数学是需要思考的学科,但愿今天的“一招制胜法”能帮不您解决一些烦恼。
再忙也要注意身体,再委屈也要学会调节自己。
在这个充满任性的年代,面对名利,你来也好,不来也好,我就在这里,我们需要平和的心里。
身体健康!工作顺利!万事如意!中考大吉!
同课章节目录
