人教版高一物理选修3-5第十六章16.4碰撞(25张ppt)
文档属性
| 名称 | 人教版高一物理选修3-5第十六章16.4碰撞(25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-29 08:03:11 | ||
图片预览







文档简介
(共25张PPT)
碰撞(1)
——制作人:某某某
碰撞
基本概念
1、碰撞:两粒子或物体间极短的相互作用
1、研究过程:碰撞过程(碰撞前一瞬间→碰撞后一瞬间)
注意理解
2、基本特点:碰撞过程时间极短,可认为碰撞前后两物体的位置都没有变化
第一种分类
1、一维碰撞:物体碰撞前沿同一直线运动,碰撞之后仍沿这条直线运动(又称正碰or对心碰撞)
产生条件:碰前速度方向与两球心连线在同一条直线上(例如:台球中的直杆…)
碰撞的分类
碰撞
思考与讨论?
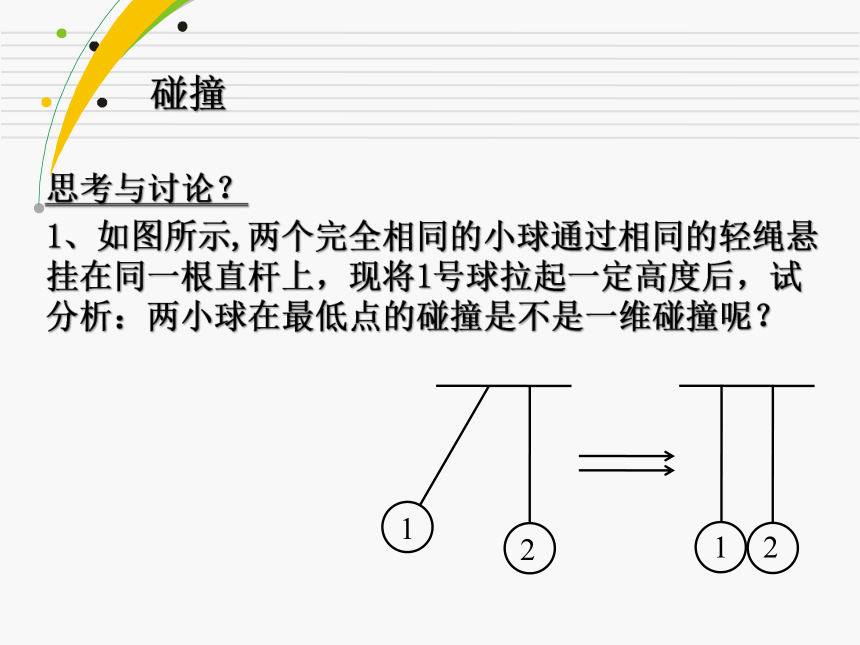
1、如图所示,两个完全相同的小球通过相同的轻绳悬挂在同一根直杆上,现将1号球拉起一定高度后,试分析:两小球在最低点的碰撞是不是一维碰撞呢?
2、二维碰撞(又称:非对心碰撞or斜碰)
产生条件:碰前速度方向与两球心连线不在同一条直线上(例如:台球的擦边…)
碰撞的分类
第二种分类:从能量损耗的角度进行分类
2、一般碰撞:存在动能损失,碰后发生分离的碰撞
碰撞的分类
3、完全非弹性碰撞:碰撞之后黏在一起→一起运动
※特点分析:a、碰后两物体共速;b、完全非弹性碰撞的能量损耗最大
1、弹性碰撞:无动能损失的碰撞
※特点分析:碰撞过程满足机械能守恒
简要总结
2、所以若要求碰撞过程中某些参量的范围,可以直接先求两个临界状态
碰撞的分类
1、弹性碰撞与完全非弹性碰撞是碰撞的两个临界状态,而一般碰撞则位于两者之间
碰撞
基本概念
1、碰撞:两粒子或物体间极短的相互作用
基本特点
1、相互作用时间极短(Δt≈0)
2、Δt≈0→碰撞前后物体的位置几乎不变
3、碰撞后系统的动能≤碰前动能
碰撞
思考与讨论?
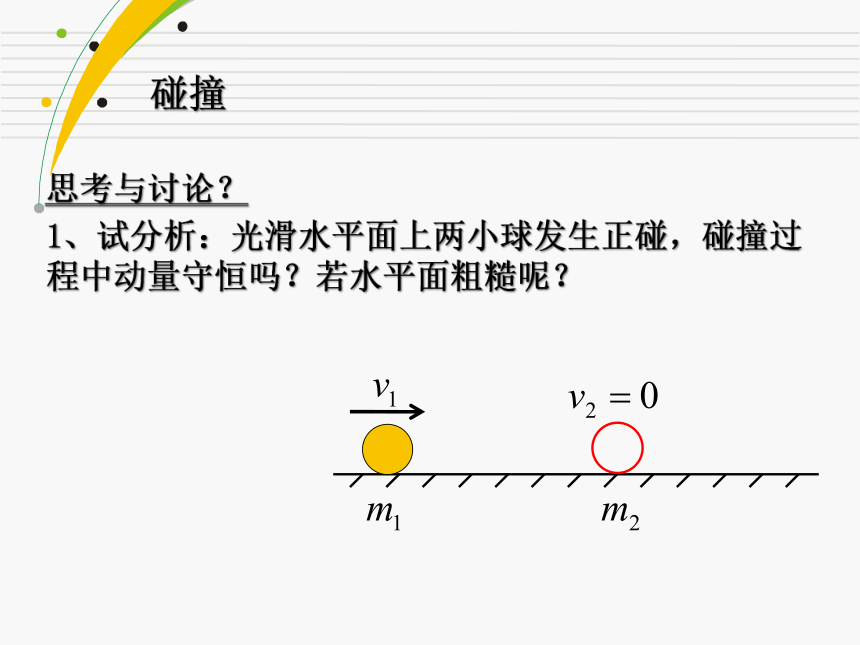
1、试分析:光滑水平面上两小球发生正碰,碰撞过程中动量守恒吗?若水平面粗糙呢?
碰撞
思考与讨论?
2、试分析:若两小球在空中发生竖直方向上的正碰,那么在碰撞过程中动量是否守恒呢?
归纳总结
※在碰撞过程中由于内力远远大于外力,导致碰撞过程所用时间极短,因此可以忽略外力带来的冲量即合外力的冲量为零→满足动量守恒定律(与爆炸类似)
弹性碰撞——定量计算
思考与讨论?
1、如图所示:在光滑水平面上两小球发生对心碰撞,若为弹性碰撞,则碰后两小球的速度为多少?
碰撞
定量计算
规定以向右的方向为正方向
由动量守恒定律有:
由机械能守恒定律有:
碰撞
数学处理
※核心思想:将表示同一个物体的量移到同一边
用下式除以上式:
(联立两式即可)
碰撞
定量计算
联立以上式子有:
分类讨论
速度交换
前提:弹性碰撞
碰撞
思考与讨论?
1、如图所示:两个个完全相同的小球通过相同的轻绳悬挂在同一根直杆上,现将1号球拉起一定高度后释放,会发生什么呢?(小球在最低点发生弹性正碰)
碰撞
实验演示
2、如图所示:六个完全相同的小球通过相同的轻绳悬挂在同一根直杆上,现将1号球拉起一定高度后释放,会发生什么呢?(小球在最低点发生弹性正碰)
碰撞
定量计算
联立以上式子有:
分类讨论
螳臂当车
碰撞
定量计算
联立以上式子有:
分类讨论
“撞墙”
随堂练习
思考与讨论?
1、在光滑的水平面上,质量为m1的小球A以速度v0向右运动。在小球A的前方O点有一质量为m2的小球B处于静止状态,如图所示。小球A与小球B发生正碰后小球A、B均向右运动。小球B被在Q点处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO。假设小球间 的碰撞及小球与墙壁之间的碰撞都是弹性碰撞,求两小球质量之比m1/m2?
经典模型
思考与讨论?
1、试分析:两小球的运动情况如何?
经典模型
思考与讨论?
2、试分析:如何来求弹性势能的最大值呢?
随堂练习
思考与讨论?
3、质量为M的小车静止在光滑水平面上,右端固定一轻质弹簧。质量为m的物块以水平向右的初速度v0从小车左端滑上小车,最后物块恰好没有从小车上滑落。已知物块与小车间的动摩擦因数为μ,求弹簧可能储存的最大弹性势能EP
补充:一点细节问题
思考与讨论?
1、试分析:A与B的碰撞对C有没有影响?如何写动量守恒呢?
2、若AB之间为完全非弹性碰撞,则从一开始到三者共速的全过程中动量是否守恒?机械能是否守恒呢?
补充:一点细节问题
思考与讨论?
3、试分析:A与B的碰撞对C有没有影响?如何写动量守恒呢?
补充:一点细节问题
思考与讨论?
4、试分析:A与B的碰撞对C有没有影响?如何写动量守恒呢?
5、若AB之间为完全非弹性碰撞,则从一开始到三者共速的全过程中动量是否守恒?机械能是否守恒呢?
碰撞(1)
——制作人:某某某
碰撞
基本概念
1、碰撞:两粒子或物体间极短的相互作用
1、研究过程:碰撞过程(碰撞前一瞬间→碰撞后一瞬间)
注意理解
2、基本特点:碰撞过程时间极短,可认为碰撞前后两物体的位置都没有变化
第一种分类
1、一维碰撞:物体碰撞前沿同一直线运动,碰撞之后仍沿这条直线运动(又称正碰or对心碰撞)
产生条件:碰前速度方向与两球心连线在同一条直线上(例如:台球中的直杆…)
碰撞的分类
碰撞
思考与讨论?
1、如图所示,两个完全相同的小球通过相同的轻绳悬挂在同一根直杆上,现将1号球拉起一定高度后,试分析:两小球在最低点的碰撞是不是一维碰撞呢?
2、二维碰撞(又称:非对心碰撞or斜碰)
产生条件:碰前速度方向与两球心连线不在同一条直线上(例如:台球的擦边…)
碰撞的分类
第二种分类:从能量损耗的角度进行分类
2、一般碰撞:存在动能损失,碰后发生分离的碰撞
碰撞的分类
3、完全非弹性碰撞:碰撞之后黏在一起→一起运动
※特点分析:a、碰后两物体共速;b、完全非弹性碰撞的能量损耗最大
1、弹性碰撞:无动能损失的碰撞
※特点分析:碰撞过程满足机械能守恒
简要总结
2、所以若要求碰撞过程中某些参量的范围,可以直接先求两个临界状态
碰撞的分类
1、弹性碰撞与完全非弹性碰撞是碰撞的两个临界状态,而一般碰撞则位于两者之间
碰撞
基本概念
1、碰撞:两粒子或物体间极短的相互作用
基本特点
1、相互作用时间极短(Δt≈0)
2、Δt≈0→碰撞前后物体的位置几乎不变
3、碰撞后系统的动能≤碰前动能
碰撞
思考与讨论?
1、试分析:光滑水平面上两小球发生正碰,碰撞过程中动量守恒吗?若水平面粗糙呢?
碰撞
思考与讨论?
2、试分析:若两小球在空中发生竖直方向上的正碰,那么在碰撞过程中动量是否守恒呢?
归纳总结
※在碰撞过程中由于内力远远大于外力,导致碰撞过程所用时间极短,因此可以忽略外力带来的冲量即合外力的冲量为零→满足动量守恒定律(与爆炸类似)
弹性碰撞——定量计算
思考与讨论?
1、如图所示:在光滑水平面上两小球发生对心碰撞,若为弹性碰撞,则碰后两小球的速度为多少?
碰撞
定量计算
规定以向右的方向为正方向
由动量守恒定律有:
由机械能守恒定律有:
碰撞
数学处理
※核心思想:将表示同一个物体的量移到同一边
用下式除以上式:
(联立两式即可)
碰撞
定量计算
联立以上式子有:
分类讨论
速度交换
前提:弹性碰撞
碰撞
思考与讨论?
1、如图所示:两个个完全相同的小球通过相同的轻绳悬挂在同一根直杆上,现将1号球拉起一定高度后释放,会发生什么呢?(小球在最低点发生弹性正碰)
碰撞
实验演示
2、如图所示:六个完全相同的小球通过相同的轻绳悬挂在同一根直杆上,现将1号球拉起一定高度后释放,会发生什么呢?(小球在最低点发生弹性正碰)
碰撞
定量计算
联立以上式子有:
分类讨论
螳臂当车
碰撞
定量计算
联立以上式子有:
分类讨论
“撞墙”
随堂练习
思考与讨论?
1、在光滑的水平面上,质量为m1的小球A以速度v0向右运动。在小球A的前方O点有一质量为m2的小球B处于静止状态,如图所示。小球A与小球B发生正碰后小球A、B均向右运动。小球B被在Q点处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO。假设小球间 的碰撞及小球与墙壁之间的碰撞都是弹性碰撞,求两小球质量之比m1/m2?
经典模型
思考与讨论?
1、试分析:两小球的运动情况如何?
经典模型
思考与讨论?
2、试分析:如何来求弹性势能的最大值呢?
随堂练习
思考与讨论?
3、质量为M的小车静止在光滑水平面上,右端固定一轻质弹簧。质量为m的物块以水平向右的初速度v0从小车左端滑上小车,最后物块恰好没有从小车上滑落。已知物块与小车间的动摩擦因数为μ,求弹簧可能储存的最大弹性势能EP
补充:一点细节问题
思考与讨论?
1、试分析:A与B的碰撞对C有没有影响?如何写动量守恒呢?
2、若AB之间为完全非弹性碰撞,则从一开始到三者共速的全过程中动量是否守恒?机械能是否守恒呢?
补充:一点细节问题
思考与讨论?
3、试分析:A与B的碰撞对C有没有影响?如何写动量守恒呢?
补充:一点细节问题
思考与讨论?
4、试分析:A与B的碰撞对C有没有影响?如何写动量守恒呢?
5、若AB之间为完全非弹性碰撞,则从一开始到三者共速的全过程中动量是否守恒?机械能是否守恒呢?
